24.4.1直线与圆的位置关系 导学案
图片预览



文档简介
24.4.1直线与圆的位置关系导学案
课题
直线与圆的位置关系
单元
24
学科
数学
年级
九年级
知识目标
1.使学生从具体的事例中认知和理解直线与圆的三种位置关系并能概括其定义
2.会用定义来判断直线与圆的位置关系
3.通过类比点与圆的位置关系及观察、实验等活动探究直线与圆的位置关系的数量关系及其运用。
重点难点
重点:理解直线与圆的相交、相离、相切三种位置关系.
难点:切线的性质与判定.
教学过程
知识链接
1、点和圆的位置关系有几种?
2.用数量关系如何来判断呢?
合作探究
一、教材第33页
1、观察
如果我们把太阳看成一个圆,地平线看成一条直线,那太阳在升起或降落的过程中它与地平线有几种位置关系?
2、观察圆O与直线l的公共点个数,有几种情况?
填表
二、教材第34页
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的 (如图直线l),这个唯一的公共点叫做切点(如图点A).
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
直线和圆相交: 。
直线与圆相切: 。
直线与圆相离: 。
总结:判定直线与圆的位置关系的方法有:
(1)根据定义:由________________ 的个数来判断;
(2)根据性质:由 的关系来判断。
为什么点A是切点?
总结:切线的性质: 。
三、教材34页
例1、如图,Rt△ABC的斜边AB=10cm,∠A=30°
(1)以点C为圆心作圆,当半径为多少时,AB与圆C相切?
(2)以点C为圆心,半径r分别为4cm,和5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系
四、教材35页
思考:
1.如图,经过圆上一点P,作直线与已知圆相切,如何作?能够作几条?
2.如图,经过圆外一点P,作直线与已知圆相切,如何作?能够作几条?
例2、如图,点P为圆O上任一点,过点P作直线l与圆O相切
总结:总结切线的判定定理
。
五、教材36页
例3、已知:如图,∠ABC=45°,AB是圆O的直径,AB=AC
求证:AC是圆O的切线
自主尝试
1.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
2.在Rt△ABC中,∠C=90°,AC=8cm,AB=10cm,以C为圆心,以9cm长为直径的⊙C与直线AB的位置关系为( )
A.相交 B.相离 C.相切 D.相离或相交
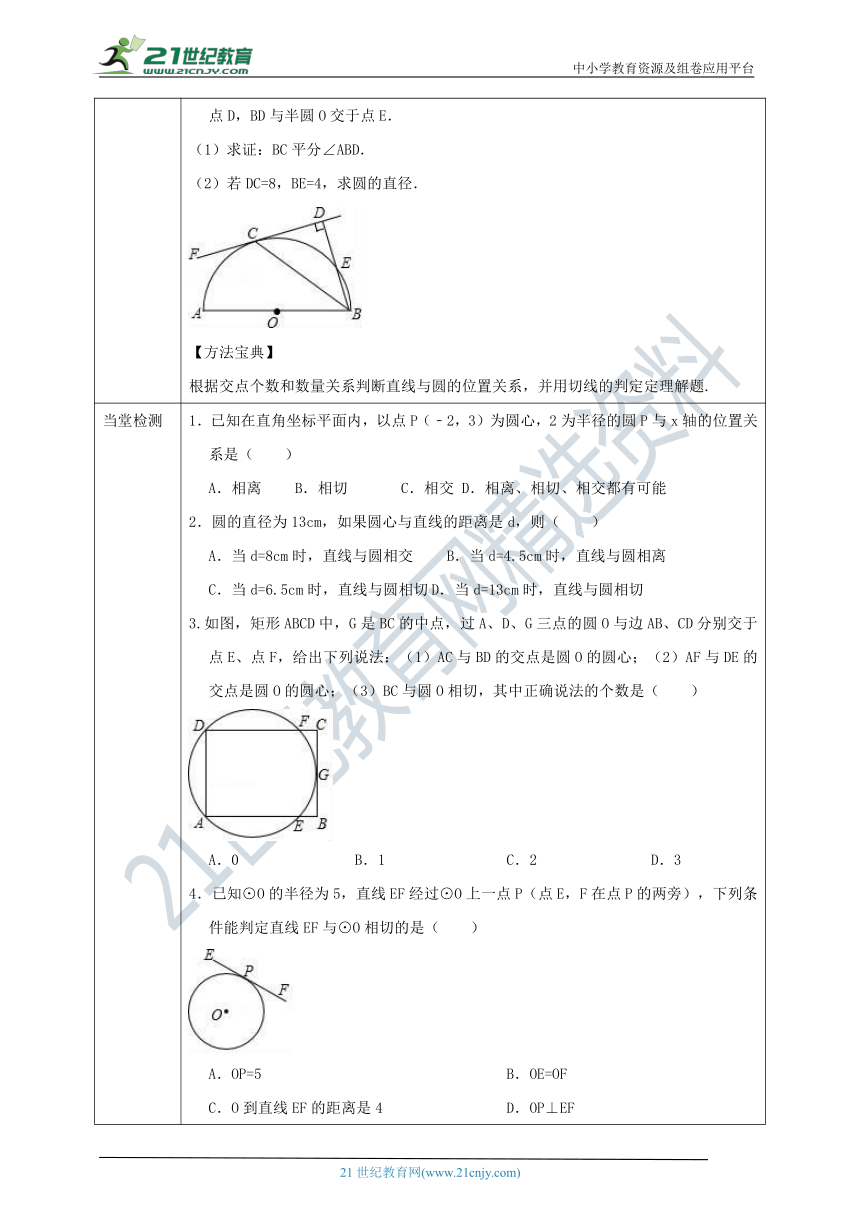
3.如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
【方法宝典】
根据交点个数和数量关系判断直线与圆的位置关系,并用切线的判定定理解题.
当堂检测
1.已知在直角坐标平面内,以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是( )
A.相离 B.相切 C.相交 D.相离、相切、相交都有可能
2.圆的直径为13cm,如果圆心与直线的距离是d,则( )
A.当d=8cm时,直线与圆相交 B.当d=4.5cm时,直线与圆相离
C.当d=6.5cm时,直线与圆相切 D.当d=13cm时,直线与圆相切
3.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
A.0 B.1 C.2 D.3
4.已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
5.如图,直线PA是⊙O的切线,AB是过切点A的直径,连接PO交⊙O于点C,连接BC,若∠ABC=25°,则∠P的度数为 .
6.如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1. A 2. C 3. C 4. D
5. 40°
6.解:(1)如图,连接OA;
∵OC=BC,AC=OB,
∴OC=BC=AC=OA.
∴△ACO是等边三角形.
∴∠O=∠OCA=60°,
∵AC=BC,
∴∠CAB=∠B,
又∠OCA为△ACB的外角,
∴∠OCA=∠CAB+∠B=2∠B,
∴∠B=30°,又∠OAC=60°,
∴∠OAB=90°,
∴AB是⊙O的切线;
(2)解:作AE⊥CD于点E,
∵∠O=60°,
∴∠D=30°.
∵∠ACD=45°,AC=OC=2,
∴在Rt△ACE中,CE=AE=;
∵∠D=30°,
∴AD=2,
∴DE=AE=,
∴CD=DE+CE=+.
课题
直线与圆的位置关系
单元
24
学科
数学
年级
九年级
知识目标
1.使学生从具体的事例中认知和理解直线与圆的三种位置关系并能概括其定义
2.会用定义来判断直线与圆的位置关系
3.通过类比点与圆的位置关系及观察、实验等活动探究直线与圆的位置关系的数量关系及其运用。
重点难点
重点:理解直线与圆的相交、相离、相切三种位置关系.
难点:切线的性质与判定.
教学过程
知识链接
1、点和圆的位置关系有几种?
2.用数量关系如何来判断呢?
合作探究
一、教材第33页
1、观察
如果我们把太阳看成一个圆,地平线看成一条直线,那太阳在升起或降落的过程中它与地平线有几种位置关系?
2、观察圆O与直线l的公共点个数,有几种情况?
填表
二、教材第34页
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的 (如图直线l),这个唯一的公共点叫做切点(如图点A).
上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?你能否用数量关系来判别直线与圆的位置关系?
直线和圆相交: 。
直线与圆相切: 。
直线与圆相离: 。
总结:判定直线与圆的位置关系的方法有:
(1)根据定义:由________________ 的个数来判断;
(2)根据性质:由 的关系来判断。
为什么点A是切点?
总结:切线的性质: 。
三、教材34页
例1、如图,Rt△ABC的斜边AB=10cm,∠A=30°
(1)以点C为圆心作圆,当半径为多少时,AB与圆C相切?
(2)以点C为圆心,半径r分别为4cm,和5cm作两个圆,这两个圆与斜边AB分别有怎样的位置关系
四、教材35页
思考:
1.如图,经过圆上一点P,作直线与已知圆相切,如何作?能够作几条?
2.如图,经过圆外一点P,作直线与已知圆相切,如何作?能够作几条?
例2、如图,点P为圆O上任一点,过点P作直线l与圆O相切
总结:总结切线的判定定理
。
五、教材36页
例3、已知:如图,∠ABC=45°,AB是圆O的直径,AB=AC
求证:AC是圆O的切线
自主尝试
1.已知⊙O的半径为4,点O到直线m的距离为3,则直线m与⊙O公共点的个数为( )
A.0个 B.1个 C.2个 D.3个
2.在Rt△ABC中,∠C=90°,AC=8cm,AB=10cm,以C为圆心,以9cm长为直径的⊙C与直线AB的位置关系为( )
A.相交 B.相离 C.相切 D.相离或相交
3.如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
【方法宝典】
根据交点个数和数量关系判断直线与圆的位置关系,并用切线的判定定理解题.
当堂检测
1.已知在直角坐标平面内,以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是( )
A.相离 B.相切 C.相交 D.相离、相切、相交都有可能
2.圆的直径为13cm,如果圆心与直线的距离是d,则( )
A.当d=8cm时,直线与圆相交 B.当d=4.5cm时,直线与圆相离
C.当d=6.5cm时,直线与圆相切 D.当d=13cm时,直线与圆相切
3.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是( )
A.0 B.1 C.2 D.3
4.已知⊙O的半径为5,直线EF经过⊙O上一点P(点E,F在点P的两旁),下列条件能判定直线EF与⊙O相切的是( )
A.OP=5 B.OE=OF
C.O到直线EF的距离是4 D.OP⊥EF
5.如图,直线PA是⊙O的切线,AB是过切点A的直径,连接PO交⊙O于点C,连接BC,若∠ABC=25°,则∠P的度数为 .
6.如图,已知A是⊙O上一点,半径OC的延长线与过点A的直线交于点B,OC=BC,AC=OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1. A 2. C 3. C 4. D
5. 40°
6.解:(1)如图,连接OA;
∵OC=BC,AC=OB,
∴OC=BC=AC=OA.
∴△ACO是等边三角形.
∴∠O=∠OCA=60°,
∵AC=BC,
∴∠CAB=∠B,
又∠OCA为△ACB的外角,
∴∠OCA=∠CAB+∠B=2∠B,
∴∠B=30°,又∠OAC=60°,
∴∠OAB=90°,
∴AB是⊙O的切线;
(2)解:作AE⊥CD于点E,
∵∠O=60°,
∴∠D=30°.
∵∠ACD=45°,AC=OC=2,
∴在Rt△ACE中,CE=AE=;
∵∠D=30°,
∴AD=2,
∴DE=AE=,
∴CD=DE+CE=+.
