24.4.2直线与圆的位置关系 导学案
图片预览

文档简介
24.4.2直线与圆的位置关系导学案
课题
直线与圆的位置关系
单元
24
学科
数学
年级
九年级
知识目标
1.了解切线长的定义.
2.掌握切线长定理,并利用它进行有关的计算.
3.在运用切线长定理的解题过程中,进一步渗透方程的思想,熟悉用代数的方法解几何题.
重点难点
重点:理解切线长定理.
难点:应用切线长定理解决问题.
教学过程
知识链接
上节课我们学习了过圆上一点作已知圆的切线(如图所示),如果点P是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
/
合作探究
一、教材第37页
1、例题
例4 、点P为圆O外一点,过点P作直线与圆O相切
总结:过一点能作圆的 条切线
切线长: 。
切线与切线长的区别与联系:
。
二、教材第38页
探究
在透明纸上画出图(1),设PA、PB是圆O的两条切线,A,B是切点,沿直线OP将图形折叠,有什么发现?
/
。
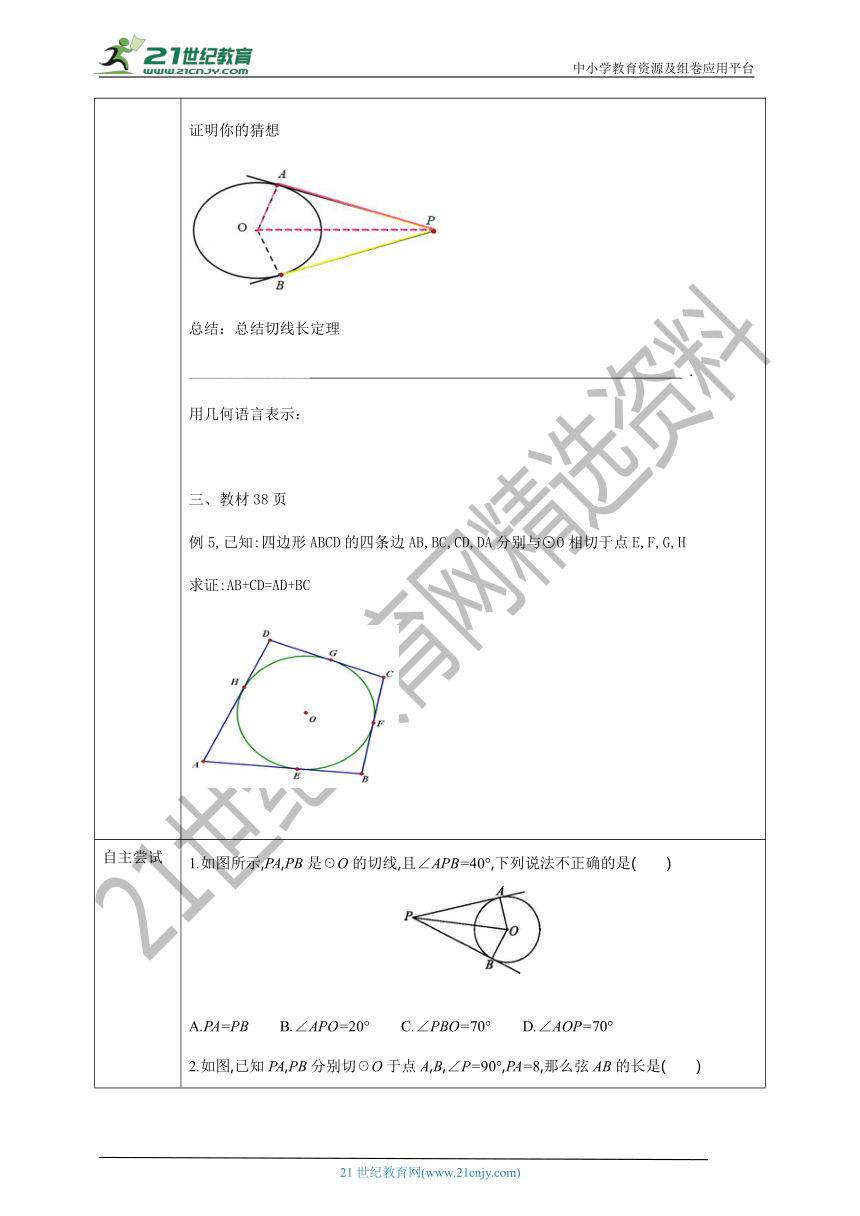
证明你的猜想
/
总结:总结切线长定理
________________ .
用几何语言表示:
三、教材38页
例5,已知:四边形ABCD的四条边AB,BC,CD,DA分别与⊙O相切于点E,F,G,H
求证:AB+CD=AD+BC
/
自主尝试
1.如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )
/
A.PA=PB B.∠APO=20° C.∠PBO=70° D.∠AOP=70°
2.如图,已知PA,PB分别切☉O于点A,B,∠P=90°,PA=8,那么弦AB的长是( )
/
A.4 B.8 C.4
2
D.8
2
3.如图,PA,PB是☉O的切线,CD切☉O于点E,△PCD的周长为12,∠P=60°.
求:(1)PA的长;
(2)∠COD的度数.
/
【方法宝典】
根据切线长定理解题.
当堂检测
1.如图,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆O,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积是( )
/
A.12 cm2 B.24 cm2 C.8 cm2 D.6 cm2
2.如图7,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E,则AD的长为( )
/
A.2.5 B.1.6 C.1.5 D.1
3.如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,若∠P=46°,则∠BAC= °
/
4.如图,☉O的半径为3 cm,点P到圆心O的距离为6 cm,经过点P引☉O的两条切线PA,PB,这两条切线的夹角为 度.?
/
5.如图,直线AB,BC,CD分别与☉O相切于点E,F,G,且AB∥CD,OB=6,OC=8.
(1)求∠BOC的度数;
(2)求BE+CG的长.
/
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1. D 2. B 3. 23 4. 60
5. 解:(1)根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBC+∠OCB=
1
2
(∠ABC+∠BCD)=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°.
(2)在Rt△BOC中,BC=
??
??
2
+??
??
2
=
6
2
+
8
2
=10,∴BE+CG=BC=10.
/
课题
直线与圆的位置关系
单元
24
学科
数学
年级
九年级
知识目标
1.了解切线长的定义.
2.掌握切线长定理,并利用它进行有关的计算.
3.在运用切线长定理的解题过程中,进一步渗透方程的思想,熟悉用代数的方法解几何题.
重点难点
重点:理解切线长定理.
难点:应用切线长定理解决问题.
教学过程
知识链接
上节课我们学习了过圆上一点作已知圆的切线(如图所示),如果点P是圆外一点,又怎么作该圆的切线呢?过圆外的一点作圆的切线,可以作几条?
/
合作探究
一、教材第37页
1、例题
例4 、点P为圆O外一点,过点P作直线与圆O相切
总结:过一点能作圆的 条切线
切线长: 。
切线与切线长的区别与联系:
。
二、教材第38页
探究
在透明纸上画出图(1),设PA、PB是圆O的两条切线,A,B是切点,沿直线OP将图形折叠,有什么发现?
/
。
证明你的猜想
/
总结:总结切线长定理
________________ .
用几何语言表示:
三、教材38页
例5,已知:四边形ABCD的四条边AB,BC,CD,DA分别与⊙O相切于点E,F,G,H
求证:AB+CD=AD+BC
/
自主尝试
1.如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )
/
A.PA=PB B.∠APO=20° C.∠PBO=70° D.∠AOP=70°
2.如图,已知PA,PB分别切☉O于点A,B,∠P=90°,PA=8,那么弦AB的长是( )
/
A.4 B.8 C.4
2
D.8
2
3.如图,PA,PB是☉O的切线,CD切☉O于点E,△PCD的周长为12,∠P=60°.
求:(1)PA的长;
(2)∠COD的度数.
/
【方法宝典】
根据切线长定理解题.
当堂检测
1.如图,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆O,过点A作半圆的切线,与半圆相切于点F,与DC相交于点E,则△ADE的面积是( )
/
A.12 cm2 B.24 cm2 C.8 cm2 D.6 cm2
2.如图7,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E,则AD的长为( )
/
A.2.5 B.1.6 C.1.5 D.1
3.如图,PA,PB是☉O的切线,A,B为切点,AC是☉O的直径,若∠P=46°,则∠BAC= °
/
4.如图,☉O的半径为3 cm,点P到圆心O的距离为6 cm,经过点P引☉O的两条切线PA,PB,这两条切线的夹角为 度.?
/
5.如图,直线AB,BC,CD分别与☉O相切于点E,F,G,且AB∥CD,OB=6,OC=8.
(1)求∠BOC的度数;
(2)求BE+CG的长.
/
小结反思
通过本节课的学习,你们有什么收获?
参考答案:
当堂检测:
1. D 2. B 3. 23 4. 60
5. 解:(1)根据切线长定理得:BE=BF,CF=CG,∠OBF=∠OBE,∠OCF=∠OCG.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∴∠OBC+∠OCB=
1
2
(∠ABC+∠BCD)=90°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°.
(2)在Rt△BOC中,BC=
??
??
2
+??
??
2
=
6
2
+
8
2
=10,∴BE+CG=BC=10.
/
