鲁教版(五四制) 六年级下5.1线段、射线、直线上课用教案
文档属性
| 名称 | 鲁教版(五四制) 六年级下5.1线段、射线、直线上课用教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 12:55:02 | ||
图片预览


文档简介
第五章 基本平面图形
1 线段、射线、直线
【教学目标】
知识与技能:
使学生在了解线段概念的基础上,理解射线和直线的概念,并能理解它们的区别与联系.
过程与方法:
通过直线、射线、线段概念的教学,培养几何想象能力和观察能力,用运动的观点看待几何图形.
情感态度与价值观:
培养学生对几何图形的兴趣,提高学习几何的积极性.
【重点难点】
重点:直线、射线、线段的概念.
难点:对直线的“无限延伸”性的理解.
【教学过程】
一、创设情境
1.请同学们阅读教材,并完成随堂练习和习题
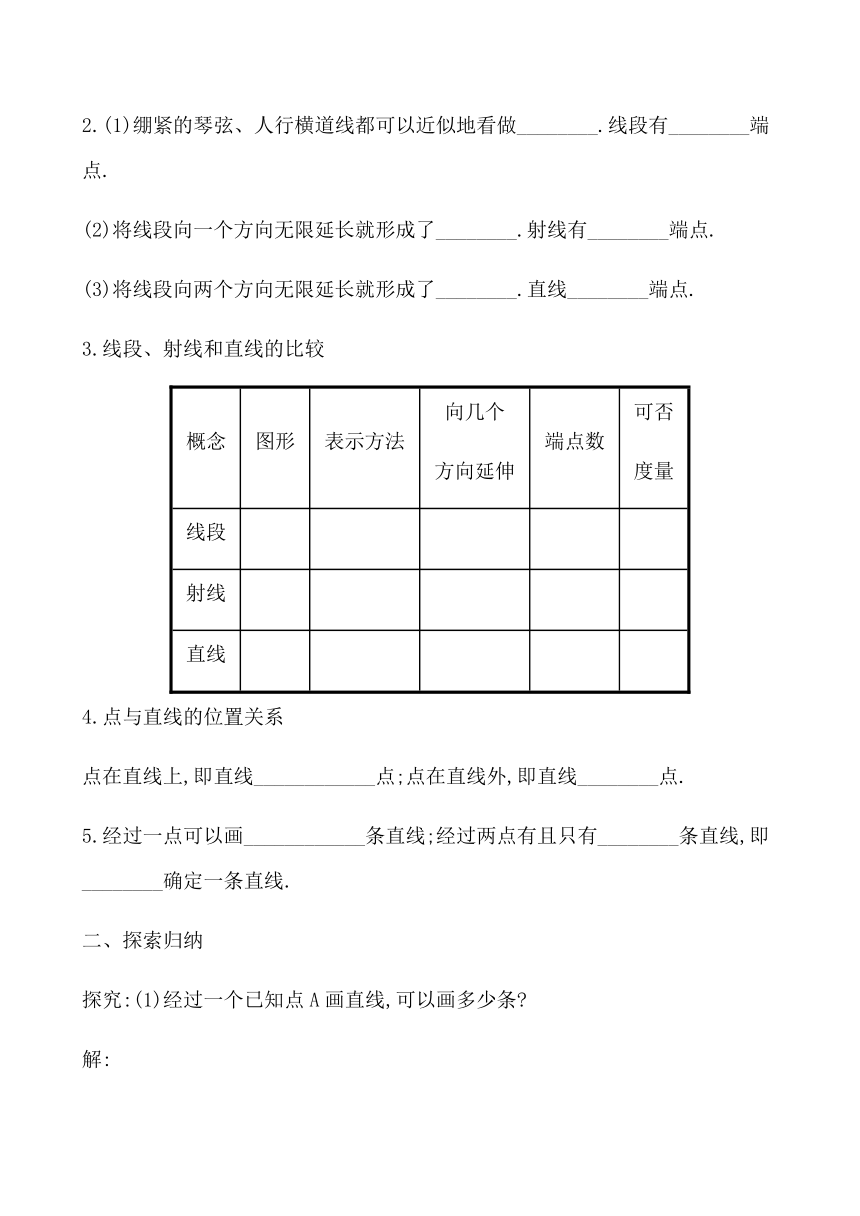
2.(1)绷紧的琴弦、人行横道线都可以近似地看做________.线段有________端点.?
(2)将线段向一个方向无限延长就形成了________.射线有________端点.?
(3)将线段向两个方向无限延长就形成了________.直线________端点.?
3.线段、射线和直线的比较
概念 图形 表示方法 向几个方向延伸 端点数 可否度量
线段
射线
直线
4.点与直线的位置关系
点在直线上,即直线____________点;点在直线外,即直线________点.?
5.经过一点可以画____________条直线;经过两点有且只有________条直线,即________确定一条直线.?
二、探索归纳
探究:(1)经过一个已知点A画直线,可以画多少条?
解:
(2)经过两个已知点A、B画直线,可以画多少条?
解:
(3)如果你想将一根细木条固定在墙上,至少需要几枚钉子?
解:
归纳:经过两点____________(“有”表示“存在性”,“只有”表示“唯一性”)一条直线.?
实践练习:如图,已知点A、B、C是直线m上的三点,请回答
(1)射线AB与射线AC是同一条射线吗?
(2)射线BA与射线BC是同一条射线吗?
(3)射线AB与射线BA是同一条射线吗?
(4)图中共有几条直线?几条射线?几条线段?
分析:线段有两个端点;射线有一个端点,向一方无限延伸;直线没有端点,向两方无限延伸
解:
三、交流反思
1.本节课你掌握了几个几何概念?
2.直线、射线和线段三者之间的关系是什么?
3.本节课应该理解哪几个关键词?
4.在表示直线、射线和线段时应注意什么?
在学生回答的基础上教师给以完善和补充,并进一步强调三者之间的关系.同时指出这三个概念是平面几何的基础.
四、检测反馈
1.线段有________个端点,射线有__________个端点,直线________端点.?
2.在直线l上取三点A、B、C,共可得____________条射线,________条线段.?
3.(1)下图可表示为线段________(或)__________或者线段________.?
(2)下图可表示为射线________.?
(3)下图可表示为直线__________或__________或者直线________.?
4.图中给出的直线、射线、线段,根据各自的性质,能相交的是 ( )
5.小明从某地乘车到成都,发现这条火车路线上共有7个站,且任意两站之间的票价都不相同,请你帮他解决下列问题.
(1)有多少种不同的票价?
(2)要准备多少种不同的车票?
五、布置作业
课本P4 1,2题
六、板书设计
1 线段、射线、直线
(一)知识回顾 (三)例题解析 (五)课堂小结
(二)观察发现 (四)课堂练习 练习设计
七、教学反思
1.本课的教学时间为1课时.
2.本设计对教材顺序稍加改动,先将直线、射线和线段的概念给出,然后再讲它们的性质.这样对于学生构建知识结构较为有利.
3.由于这节课为几何的起始课,从感性认识出发,在学生熟悉的实际生活中,抽象出几何的概念,便于认知结构的形成.
4.建议:本课时也可以将课型设计为“自学辅导式”,由学生自己讨论直线、射线和线段的概念,并寻找它们之间的区别与联系,这样更有利于发挥学生自己的主观能动性,参与意识更强,课堂更加活跃.
5.在有条件的地方,对三者关系的变化过程,应用计算机辅助教学更为生动有趣,“变”的意义更为明显.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
