北京课改版 12.3 三角形中的主要线段 课件(12张PPT)
文档属性
| 名称 | 北京课改版 12.3 三角形中的主要线段 课件(12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 257.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 14:47:04 | ||
图片预览


文档简介
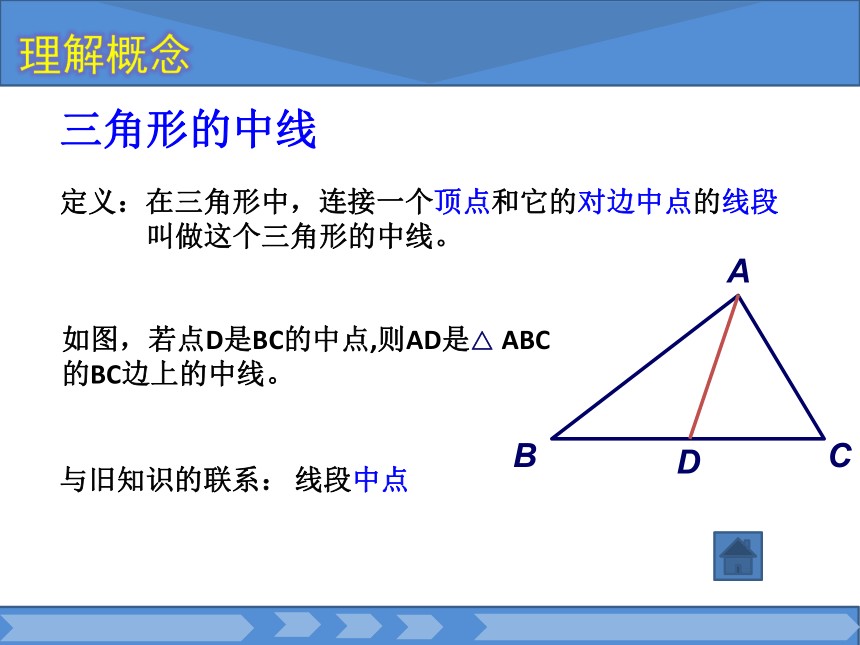
课件12张PPT。三角形研究对象主要元素相关元素三角形中的主要线段角外角边12.3 三角形中的主要线段三角形的中线定义:在三角形中,连接一个顶点和它的对边中点的线段
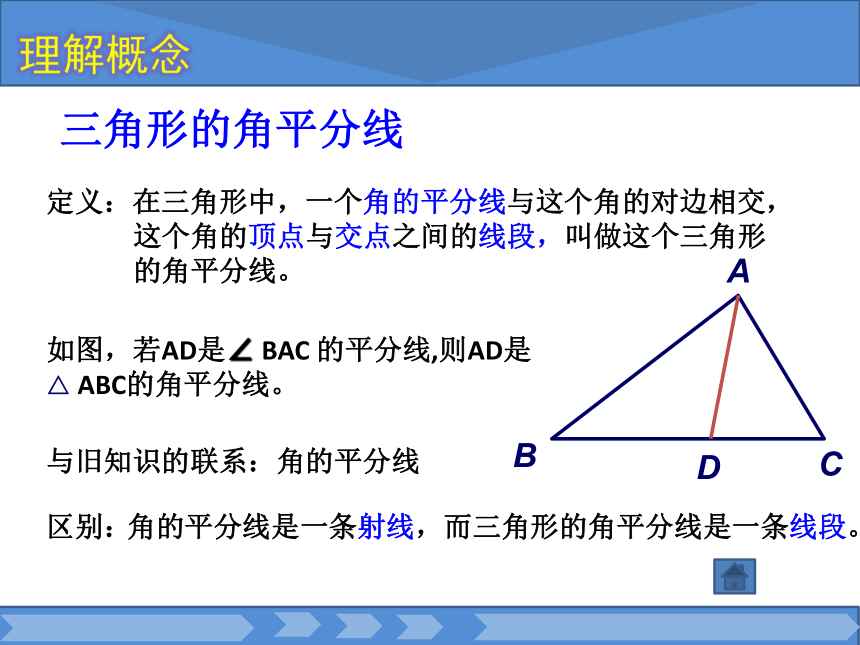
叫做这个三角形的中线。如图,若点D是BC的中点,则AD是△ ABC的BC边上的中线。与旧知识的联系:线段中点理解概念三角形的角平分线定义:在三角形中,一个角的平分线与这个角的对边相交,
这个角的顶点与交点之间的线段,叫做这个三角形
的角平分线。BCDA如图,若AD是∠ BAC 的平分线,则AD是
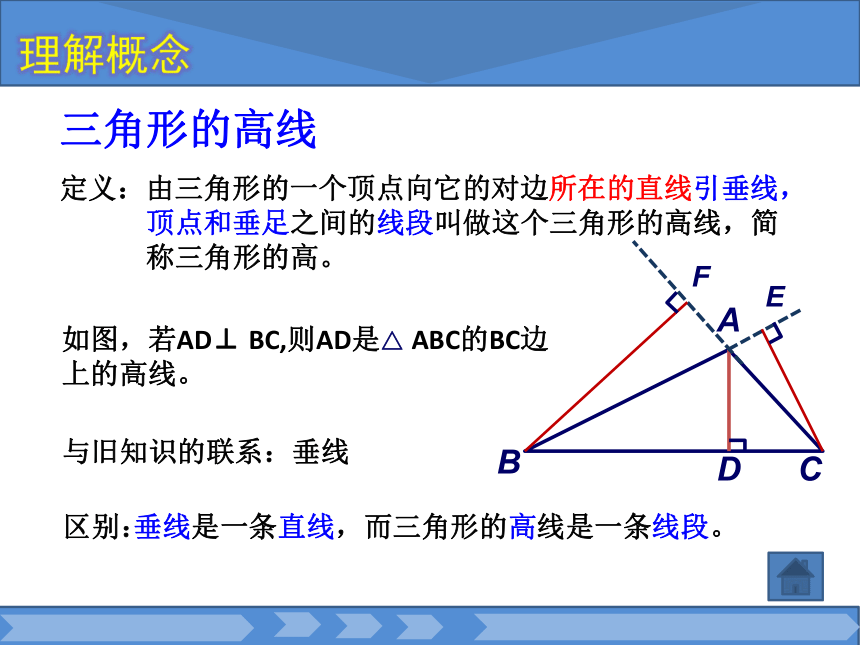
△ ABC的角平分线。与旧知识的联系:角的平分线区别:角的平分线是一条射线,而三角形的角平分线是一条线段。理解概念三角形的高线定义:由三角形的一个顶点向它的对边所在的直线引垂线,
顶点和垂足之间的线段叫做这个三角形的高线,简
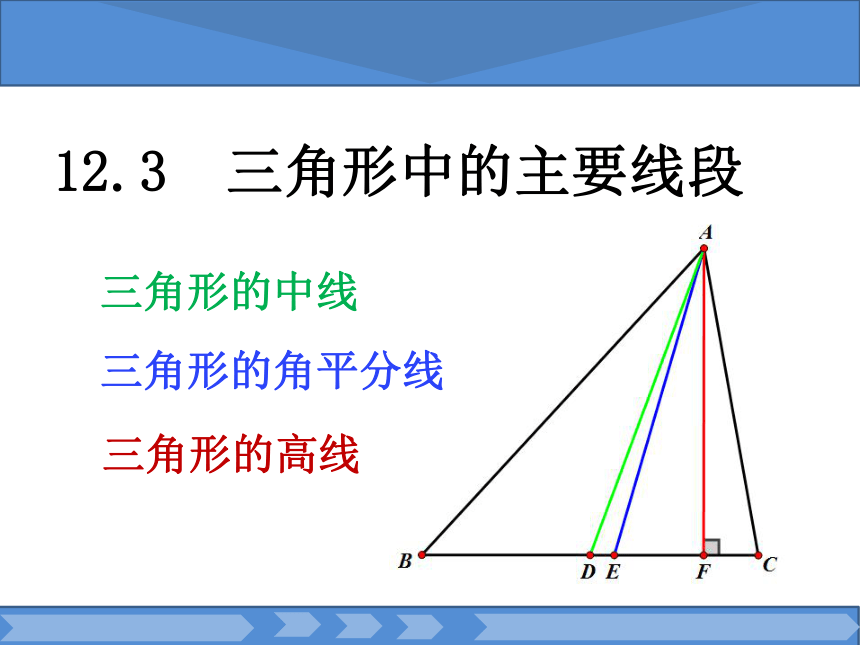
称三角形的高。BCDA如图,若AD⊥ BC,则AD是△ ABC的BC边上的高线。与旧知识的联系:垂线区别: 垂线是一条直线,而三角形的高线是一条线段。理解概念EF12.3 三角形中的主要线段三角形的中线三角形的角平分线三角形的高线探究性质 B CDA问:有一块三明治,要平均分给两个小 朋友,
如何分成面积相等的两块小三明治?
说明理由。得出三角形一条中线的性质:三角形的一条中线能把一个三角形分成两个面积
相等的三角形。答:作中线AD,则S △ ABD =S △ ACD 。理由是等底同高.三角形的一条中线能把一个三角形分成两个面积相等的三角形。三角形一条中线的性质:问:除了中线AD,还有其它的线段
也能把△ ABC 分成两个面积相
等的三角形吗,共有几种分法? BCDAE思考:两条中线相交有一个交点,三条中线可能有几个交点?
结论与三角形的形状有关吗?请同学们拿出已准备好的不同三角形形状的纸板,分别在锐角三角形、直角三角和钝角三角形纸板上画出三条中线,然后观察交点情况。得出结论:三角形的三条中线有一个交点 ,
都在这个三角形的内部,与三角形的形状无关。(三角形的重心 )
三角形三条中线性质:三角形的三条中线有一个交点,都 在
三角形的内部,与三角形的形状无关。问:三角形的三条角平分线、三条高线是否也能交于三角形
内部一点?与三角形的形状有关吗?请同学们再次拿起三角形纸板,在另一面画出三条角平分线,然后观察交点情况 ,探究完三角形三条角平分线的性质后再分别在学案上画出锐角三角形、直角三角和钝角三角形的三条高线,观察不同形状三角形所画高线的位置及所在直线的交点情况,最后小组交流总结。
得出结论:三角形的三条角平分线也能交于三角形内部一点,
与三角形的形状无关。三角形三条角平分线性质:三角形的三条角平分线有一个交点,
都在三角形的内部,与三角形的形状无关。得出结论:三角形的三条高线不一定在三角形内部,
具体位置和交点情况与三角形的形状有关。三角形的三条高线的性质:所在直线交点个数位置钝角三角形直角三角形锐角三角形内部一个三角形的三条高线所在直线交于一点三角形内部直角顶点处三角形外部不同形状三角形的三条高线一条在内部,两条在直角边上一条在内部,两条在外部一个一个所在直线交点的位置高线位置及交点情况要分类讨论:小结: 三角形的中线、角平分线和高线的相同点与不同点相同点:都是线段,都有三条,所在直线都分别交于同一点。不同点:高线的位置和所在直线交点的情况与三角形的形状有关,要分类讨论。三角形的一条中线能把任意一个三角形分成两个面积相等的三角形,角平分线和高线不能。
叫做这个三角形的中线。如图,若点D是BC的中点,则AD是△ ABC的BC边上的中线。与旧知识的联系:线段中点理解概念三角形的角平分线定义:在三角形中,一个角的平分线与这个角的对边相交,
这个角的顶点与交点之间的线段,叫做这个三角形
的角平分线。BCDA如图,若AD是∠ BAC 的平分线,则AD是
△ ABC的角平分线。与旧知识的联系:角的平分线区别:角的平分线是一条射线,而三角形的角平分线是一条线段。理解概念三角形的高线定义:由三角形的一个顶点向它的对边所在的直线引垂线,
顶点和垂足之间的线段叫做这个三角形的高线,简
称三角形的高。BCDA如图,若AD⊥ BC,则AD是△ ABC的BC边上的高线。与旧知识的联系:垂线区别: 垂线是一条直线,而三角形的高线是一条线段。理解概念EF12.3 三角形中的主要线段三角形的中线三角形的角平分线三角形的高线探究性质 B CDA问:有一块三明治,要平均分给两个小 朋友,
如何分成面积相等的两块小三明治?
说明理由。得出三角形一条中线的性质:三角形的一条中线能把一个三角形分成两个面积
相等的三角形。答:作中线AD,则S △ ABD =S △ ACD 。理由是等底同高.三角形的一条中线能把一个三角形分成两个面积相等的三角形。三角形一条中线的性质:问:除了中线AD,还有其它的线段
也能把△ ABC 分成两个面积相
等的三角形吗,共有几种分法? BCDAE思考:两条中线相交有一个交点,三条中线可能有几个交点?
结论与三角形的形状有关吗?请同学们拿出已准备好的不同三角形形状的纸板,分别在锐角三角形、直角三角和钝角三角形纸板上画出三条中线,然后观察交点情况。得出结论:三角形的三条中线有一个交点 ,
都在这个三角形的内部,与三角形的形状无关。(三角形的重心 )
三角形三条中线性质:三角形的三条中线有一个交点,都 在
三角形的内部,与三角形的形状无关。问:三角形的三条角平分线、三条高线是否也能交于三角形
内部一点?与三角形的形状有关吗?请同学们再次拿起三角形纸板,在另一面画出三条角平分线,然后观察交点情况 ,探究完三角形三条角平分线的性质后再分别在学案上画出锐角三角形、直角三角和钝角三角形的三条高线,观察不同形状三角形所画高线的位置及所在直线的交点情况,最后小组交流总结。
得出结论:三角形的三条角平分线也能交于三角形内部一点,
与三角形的形状无关。三角形三条角平分线性质:三角形的三条角平分线有一个交点,
都在三角形的内部,与三角形的形状无关。得出结论:三角形的三条高线不一定在三角形内部,
具体位置和交点情况与三角形的形状有关。三角形的三条高线的性质:所在直线交点个数位置钝角三角形直角三角形锐角三角形内部一个三角形的三条高线所在直线交于一点三角形内部直角顶点处三角形外部不同形状三角形的三条高线一条在内部,两条在直角边上一条在内部,两条在外部一个一个所在直线交点的位置高线位置及交点情况要分类讨论:小结: 三角形的中线、角平分线和高线的相同点与不同点相同点:都是线段,都有三条,所在直线都分别交于同一点。不同点:高线的位置和所在直线交点的情况与三角形的形状有关,要分类讨论。三角形的一条中线能把任意一个三角形分成两个面积相等的三角形,角平分线和高线不能。
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
