12.11 勾股定理 课件(35张PPT)
文档属性
| 名称 | 12.11 勾股定理 课件(35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-19 00:00:00 | ||
图片预览







文档简介
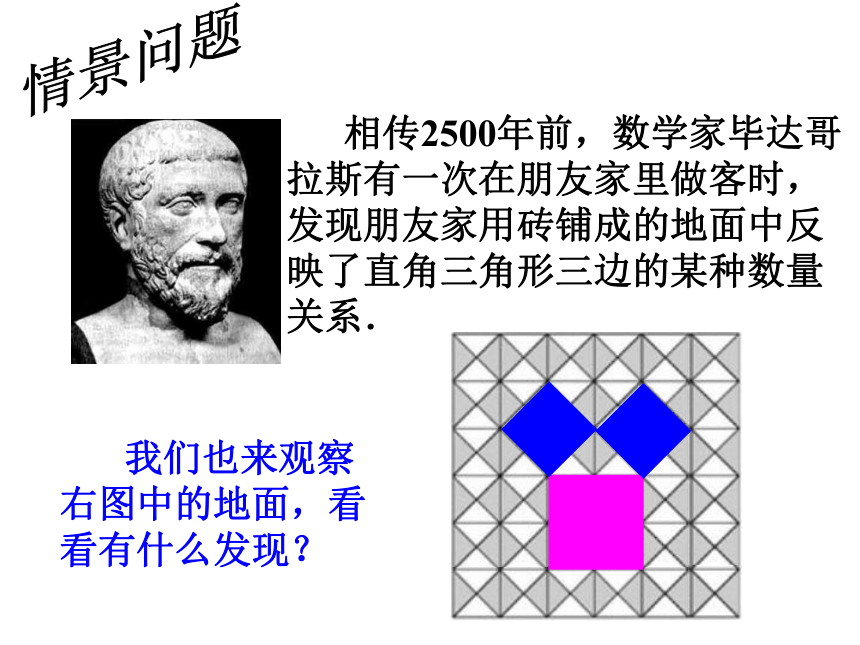
课件35张PPT。12.11 勾股定理北京版.八年级数学上册 相传2500年前,数学家毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现?情景问题 相传2500年前,毕达哥拉斯有
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
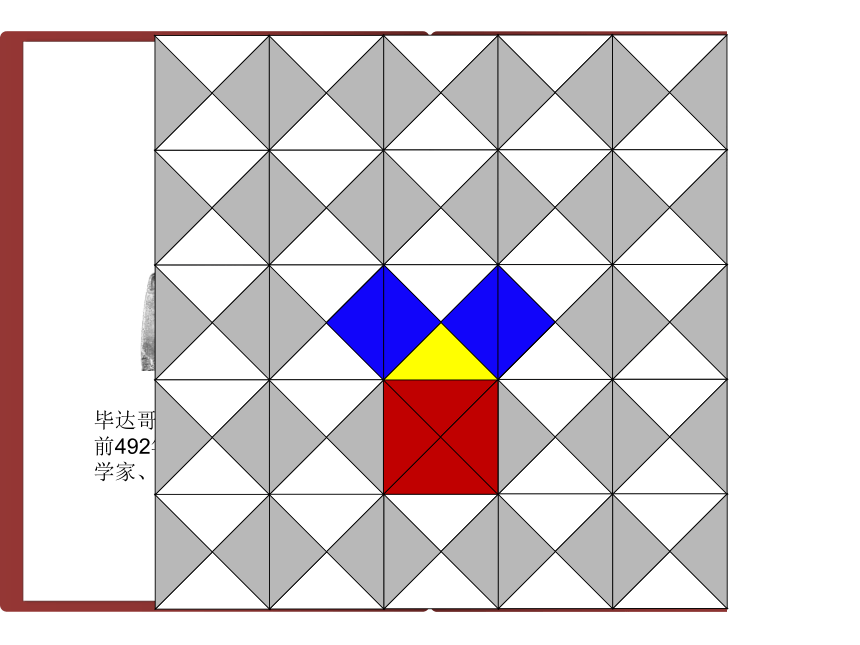
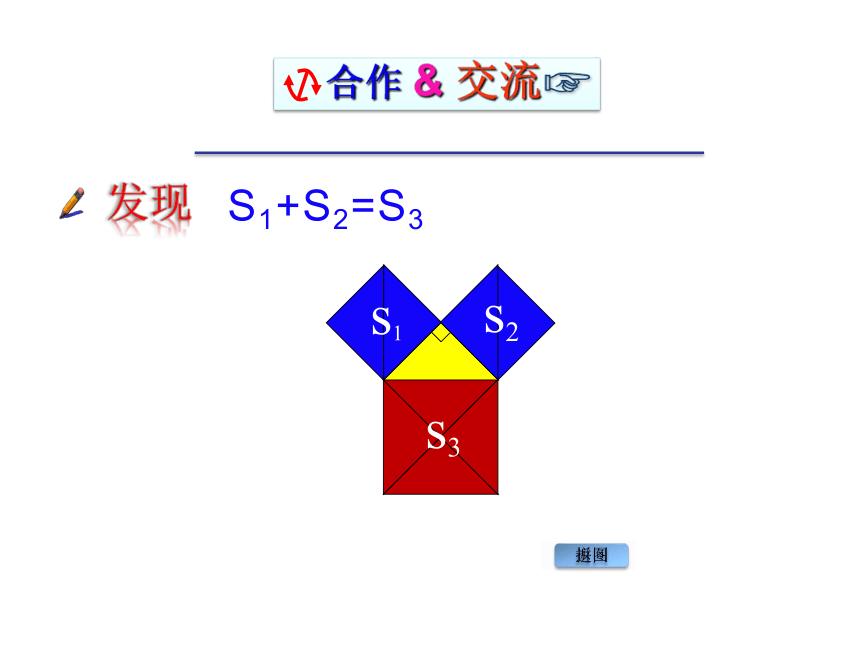
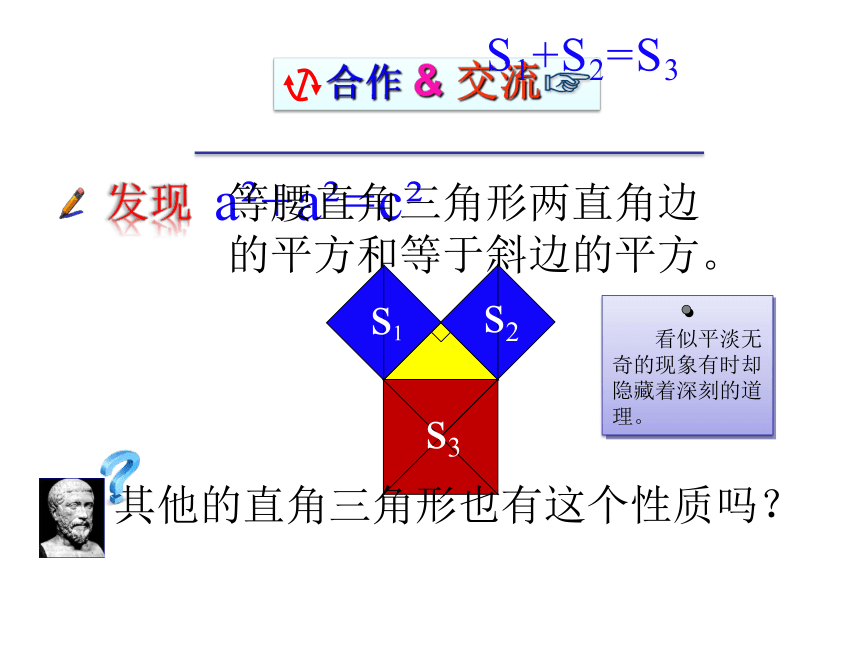
角形三边的某种数量关系。S1+S2=S3发现返回拼图s1s2s3S1+S2=S3aaca2+a2=c2等腰直角三角形两直角边
的平方和等于斜边的平方。发现其他的直角三角形也有这个性质吗?实践:(1)请同学们两人合作,画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出斜边AB的长。你会有什么发现?和你同组同学交流你的发现。
(2)对于直角三角形三边关系,你又有什么猜想? 命题: 如果直角三角形的两直角
边长分别为a,b,斜边长为c,
那么a2+b2=c2 。返回主界面 我们猜想:拼法1拼法21、拿出准备好的四个全等的直角三角形
(设两条直角边分别为a,b,斜边为c);2、小组合作用这四个直角三角形拼成一个
正方形吗?(拼出的正方形中间可以是空
的)拼一拼试试看;3、能否就拼出的图说明a2+b2=c2 ?拼图 活动 ? 赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
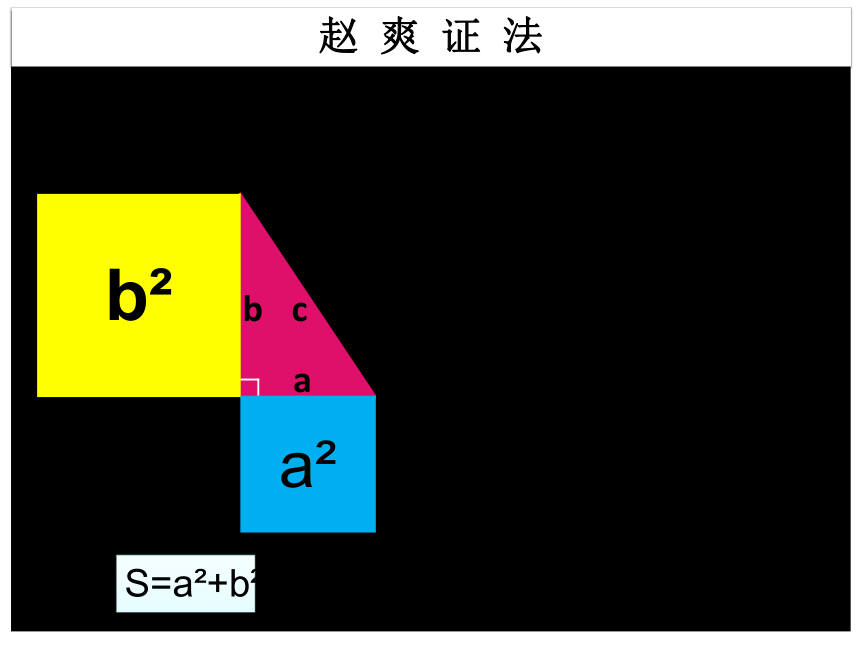
b2a2S=a2+b2赵 爽 证 法S=a2+b2赵 爽 证 法cabcba赵 爽 证 法剪拼abbacccc剪拼返回赵 爽 证 法S=a2+b2S=c2a2+b2=c2赵 爽 证 法2ab+c2(a+b)2=a2+b2=c2ABCcababcbabacc拼法1拼法2 ABCcab2ab+(b-a)2=c2a2+b2=c2abcC返回主界面 拼法1拼法2 你能用此图证明勾有股定理吗?加菲尔德( 1831 -1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。返回主界面 ?例题:AB=8?1、直角三角形中两条直角边长分别为1,1,求斜边长.练习:??图1图2图3??? 直角三角形中,已知两条边长分别为2,5,求第三条边的长.提 高:课堂小结: 本节课我们学习了哪些内容?
主要用的什么方法学习的?
你的收获是什么?课堂反馈①求下列图中字母所表示的正方形的面积
400225AB22581②X=__________62x③如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。ABCD7cm再 见! 等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x), 由勾股定理得:
x2+82=(16-x)2即x2+64=256-32x+x2∴ x=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48拓展延伸 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活,下面让我们一起来了解有关于勾股定理及其证明的一些课外知识。延伸1延伸2延伸3延伸4 返回主界面 假如我们一旦和外星人见面,该使用什么语言呢?中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍的。延伸1延伸2延伸3延伸4 返回主界面 神
奇
的
毕
达
哥
拉
斯
树延伸1延伸2延伸3延伸4 返回主界面 出入相补刘徽(生于公元三世纪)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以“出入相补”的原理来证明“勾股定理”。后人称该图为“青朱入出图”。延伸1延伸2延伸3延伸4 ……….. abc青
朱
出
入
图延伸1延伸2延伸4 返回主界面 延伸3 美国总统的证明加菲尔德( 1831 ? 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。延伸1延伸2延伸3延伸4 aabbcc延伸1延伸2延伸3延伸4 返回主界面
一次在朋友家做客时,发现朋友家
的用砖铺成的地面中反映了直角三
角形三边的某种数量关系。S1+S2=S3发现返回拼图s1s2s3S1+S2=S3aaca2+a2=c2等腰直角三角形两直角边
的平方和等于斜边的平方。发现其他的直角三角形也有这个性质吗?实践:(1)请同学们两人合作,画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出斜边AB的长。你会有什么发现?和你同组同学交流你的发现。
(2)对于直角三角形三边关系,你又有什么猜想? 命题: 如果直角三角形的两直角
边长分别为a,b,斜边长为c,
那么a2+b2=c2 。返回主界面 我们猜想:拼法1拼法21、拿出准备好的四个全等的直角三角形
(设两条直角边分别为a,b,斜边为c);2、小组合作用这四个直角三角形拼成一个
正方形吗?(拼出的正方形中间可以是空
的)拼一拼试试看;3、能否就拼出的图说明a2+b2=c2 ?拼图 活动 ? 赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
赵爽是3世纪我国汉代的
数学家与天文学家,他在注解
《周髀算经》时,用他画的弦
图来证明了上面的命题。下面
我们就来看看他是怎样证明的。
b2a2S=a2+b2赵 爽 证 法S=a2+b2赵 爽 证 法cabcba赵 爽 证 法剪拼abbacccc剪拼返回赵 爽 证 法S=a2+b2S=c2a2+b2=c2赵 爽 证 法2ab+c2(a+b)2=a2+b2=c2ABCcababcbabacc拼法1拼法2 ABCcab2ab+(b-a)2=c2a2+b2=c2abcC返回主界面 拼法1拼法2 你能用此图证明勾有股定理吗?加菲尔德( 1831 -1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。返回主界面 ?例题:AB=8?1、直角三角形中两条直角边长分别为1,1,求斜边长.练习:??图1图2图3??? 直角三角形中,已知两条边长分别为2,5,求第三条边的长.提 高:课堂小结: 本节课我们学习了哪些内容?
主要用的什么方法学习的?
你的收获是什么?课堂反馈①求下列图中字母所表示的正方形的面积
400225AB22581②X=__________62x③如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。ABCD7cm再 见! 等腰三角形底边上的高为8,周长为32,求这个三角形的面积8DABC解:设这个三角形为ABC,高为AD,设BD为x,则AB为(16-x), 由勾股定理得:
x2+82=(16-x)2即x2+64=256-32x+x2∴ x=6∴ S?ABC=BC?AD/2=2 ?6 ?8/2=48拓展延伸 我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活,下面让我们一起来了解有关于勾股定理及其证明的一些课外知识。延伸1延伸2延伸3延伸4 返回主界面 假如我们一旦和外星人见面,该使用什么语言呢?中国数学家华罗庚认为,我们可以用两个图形作为与外星人交谈的媒介,一个是“数”,另一个是“数形关系”(勾股定理)。因为这种自然图形所具备的“数形关系”在整个宇宙中是普遍的。延伸1延伸2延伸3延伸4 返回主界面 神
奇
的
毕
达
哥
拉
斯
树延伸1延伸2延伸3延伸4 返回主界面 出入相补刘徽(生于公元三世纪)
三国魏晋时代人。
魏景元四年(即 263 年)为古籍《九章算术》作注释。
在注作中,提出以“出入相补”的原理来证明“勾股定理”。后人称该图为“青朱入出图”。延伸1延伸2延伸3延伸4 ……….. abc青
朱
出
入
图延伸1延伸2延伸4 返回主界面 延伸3 美国总统的证明加菲尔德( 1831 ? 1881)
1881 年成为美国第 20 任总统
1876 年提出有关证明
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把他的证法称为“总统”证法。延伸1延伸2延伸3延伸4 aabbcc延伸1延伸2延伸3延伸4 返回主界面
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
