江苏名扬教育高一年级秋学期第二次月考数学试卷
文档属性
| 名称 | 江苏名扬教育高一年级秋学期第二次月考数学试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-22 00:00:00 | ||
图片预览




文档简介
江苏名扬教育高一年级秋学期第二次月考数学试卷
时间:120分钟 分值:150分
1、选择题(本大题12小题,每题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案涂在答题卡上)
1.下列说法中不正确的是( )
A.与任意一个向量都平行
B.任何一个非零向量都可以平行移动
C.长度不相等而方向相反的两个向量一定是共线向量
D.两个有共同起点且共线的向量其终点必相同
2.( )
A. B. C. D.
3.若是直线上的一点,且,则当时,点的位置( )
A.在线段上 B.在线段的延长线上 C.在线段的延长线上 D.不能确定
4.下列函数中在上是增函数的是( )
A. B. C. D.
5.已知,,则的值为( ).
A. B. C. D.
6.已知,则( )
A. B. C. D.
7.函数的一个单调递增区间是
A. B. C. D.
8.函数,则不等式的解集为( )
A. B. C. D.
9.若,则的取值范围是( )
A. B.
C. D. (以上)
10.函数(且)的图像是下列图像中的( )
A. B.
C. D.
11.已知函数在区间上是增函数,其在区间上恰好取得一次最大值2,则的取值范围是( )
A. B. C. D.
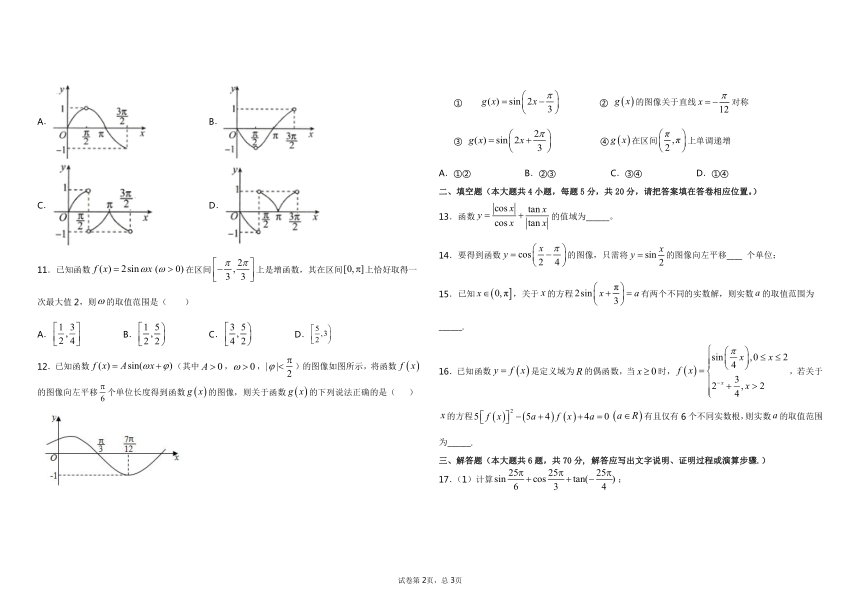
12.已知函数(其中,,)的图像如图所示,将函数的图像向左平移个单位长度得到函数的图像,则关于函数的下列说法正确的是( )
① ② 的图像关于直线对称
③ ④在区间上单调递增
A.①② B.②③ C.③④ D.①④
二、填空题(本大题共4小题,每题5分,共20分,请把答案填在答卷相应位置。)
13.函数的值域为______。
14.要得到函数的图像,只需将的图像向左平移____ 个单位;
15.已知,关于的方程有两个不同的实数解,则实数的取值范围为______.
16.已知函数是定义域为的偶函数,当时,,若关于的方程有且仅有6个不同实数根,则实数的取值范围为______.
三、解答题(本大题共6题,共70分, 解答应写出文字说明、证明过程或演算步骤.)
17.(1)计算;
(2)已知,求的值.
18.已知是第三象限角,且.
(1)求的值;
(2)求的值.
19.已知函数(且),(且)
(1)当时,求关于的不等式的解集;
(2)当时,求的值域;
(3)求关于的不等式的解集;
20.如图,一个摩天轮的半径为,轮子的最低处距离地面.如果此摩天轮按逆时针匀速转动,每转一圈,且当摩天轮上某人经过点(点与摩天轮中心的高度相同)时开始计时.
(1)求此人相对于地面的高度(单位:)关于时间(单位:)的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不小于?
21.设函数(R).
(1)若不等式在上恒成立,求的取值范围;
(2)若方程在上有四个不相等的实数根,求的取值范围.
22.某同学用“五点法”画函数在某一周期内的图像时,列表并填入的部分数据如下表:
0
0 1 0 0
0 0 0
(1)请写出上表的函数的解析式;
(2)将函数的图像向右平移个单位,再将所得图像上各点的横坐标缩小为原来的,纵坐标不变,得到函数的图像,求的解析式及的单调递增区间;
(3)在(2)的条件下,若在上恰有奇数个零点,求实数与零点个数的值.
江苏名扬教育高一年级秋学期第二次月考数学试卷参考答案
1.D
【解析】
【分析】
通过零向量的概念判断A;
通过向量的概念判断B;
通过共线向量的定义判断C;
通过共线向量的定义判断D.
【详解】
的方向是任意的,和任意向量都平行,故A正确;
向量的是既有大小又有方向的量,任意移动还是原向量,故B正确;
共线向量是方向相同或相反的向量,故C正确;
起点相同的共线向量可以是方向相反的向量,终点不一定相同,故D错误,
故选:D.
【点睛】
本题考查向量的方向问题,是基础题.
2.A
【解析】
【分析】
根据诱导公式:化简,即可得到答案.
【详解】
故选:A.
【点睛】
本考查了由诱导公式求三角函数值,能熟练使用诱导公式是解本题关键.
3.C
【解析】
【分析】
根据题意易知点不可能与,重合,故而可分为在线段上,在线段的延长线上和在线段的延长线上三种情形逐一分析即可.
【详解】
根据题意易知点不可能与,重合,
当在线段上时,;
当在线段的延长线上时,;
当在线段的延长线上时,;
故选:C.
【点睛】
本题主要考查定比分点分有向线段成的比的定义,把它转化为线段的长度比的相反数,数形结合是解题的关键,属于中档题.
4.D
【解析】
【分析】
分别根据函数的单调性进行判定即可得到结论.
【详解】
对于A选项:在上是减函数,不满足条件.
对于B选项:在上是减函数,不满足条件.
对于C选项:,令t=2x,当时,此时y=sint在上不单调,不满足条件.
对于D选项:,当时,此时y=cost在上是增函数,满足条件.
故选D.
【点睛】
本题主要考查三角函数的单调性,要求熟练掌握三角函数的图象.
5.B
【解析】
【分析】
利用同角三角函数的基本关系,求得的值.
【详解】
因为,解得:或,
因为,所以.
故选:B.
【点睛】
本题考查同角三角函数的基本关系,考查基本运算求解能力,求解时注意考虑的取值范围,防止出现符号错误.
6.D
【解析】
【分析】
观察可知,,则由诱导公式可求得
【详解】
∵,
故选:D.
【点睛】
本题考查诱导公式的用法,属于基础题
7.A
【解析】
【分析】
首先由诱导公式对函数的解析式进行恒等变形,然后求解其单调区间即可.
【详解】
函数的解析式即:,
其单调增区间满足:,
解得:,
令可得函数的一个单调递增区间为.
故选:A.
【点睛】
本题主要考查诱导公式的应用,三角函数单调区间的求解等知识,意在考查学生的转化能力和计算求解能力.
8.A
【解析】
【分析】
先根据分段函数转化为两个不等式组,解得结果.
【详解】
因为,所以或
因此或,或,即
故选:A
【点睛】
本题考查分段函数性质以及解指对数不等式,考查基本分析求解能力,属中档题.
9.D
【解析】
【分析】
根据,左边式子上下分之,分母分别乘,,所以cosx<0,解出x的取值范围即可
【详解】
因为,
所以,
所以cosx<0,解得: (以上),故选:D
【点睛】
本题主要化简三角函数等式,求解x取值范围
10.C
【解析】
【分析】
将函数表示为分段函数的形式,由此确定函数图像.
【详解】
依题意,.由此判断出正确的选项为C.
故选C.
【点睛】
本小题主要考查三角函数图像的识别,考查分段函数解析式的求法,考查同角三角函数的基本关系式,属于基础题.
11.A
【解析】
【分析】
根据函数的单调性得到,又因为在区间上恰好取得一次最大值,进而得到两者取交集即可.
【详解】
函数 在区间上是增函数,
故得到
当时,,函数在区间上恰好取得一次最大值,故得到
综上:
故答案为:A.
【点睛】
这个题目考查了三角函数的单调性的应用以及三角函数最值的求法,属于基础题. 在研究函数的单调性和最值时,一般采用的是整体思想,将ω x +φ看做一个整体,地位等同于sinx中的x.
12.B
【解析】
【分析】
根据图像得到表达式,再利用平移得到表达式,依次判断四个选项的正误,得到答案.
【详解】
函数(其中,,)
根据图像知:
将函数的图像向左平移个单位长度得到函数的图像
故①错误③正确
时是对称轴,②正确
在区间上先增后减,④错误
故答案选B
【点睛】
本题考查了根据图像求三角函数表达式,三角函数的平移,三角函数的对称抽和单调性,考查知识点较多,意在锻炼学生的综合应用能力.
13.
【解析】
【分析】
根据三角函数值在各象限的符号,讨论去掉绝对值,即可求出.
【详解】
由题意可知,角的终边不可能在坐标轴上,所以分四类:
当角的终边在第一象限,则,所以;
当角的终边在第二象限,则,所以;
当角的终边在第三象限,则,所以;
当角的终边在第四象限,则,所以;
故答案为:.
【点睛】
本题主要考查三角函数值在各象限的符号.
14.
【解析】
【分析】
由条件利用诱导公式,函数的图像变化规律,可得结论.
【详解】
将函数的图像上所有点向左平移个单位纵坐标不变,可得函数的图像.
故答案为:
【点睛】
本题主要考查诱导公式的应用、函数的图像变化规律,属于基础题.
15.
【解析】
【分析】
在同一坐标中,做出函数,,的图象,利用数形结合根据交点个数即可求解
【详解】
令,,,作出的图象如图所示.若
在上有两个不同的实数解,则与应有两个不同的交点,所以.
答案:
【点睛】
本题主要考查了函数与方程,正弦型函数图象,数形结合的思想方法,属于中档题.
16.0<a≤或a.
【解析】
【分析】
运用偶函数的性质,作出函数f(x)的图象,由5[f(x)]2﹣(5a+4)f(x)+4a=0,解得f(x)=a或f(x),结合图象,分析有且仅有6个不同实数根的a的情况,即可得到a的范围.
【详解】
函数是定义域为的偶函数,作出函数f(x)的图象如图:
关于x的方程5[f(x)]2﹣(5a+4)f(x)+4a=0,
解得f(x)=a或f(x),
当0≤x≤2时,f(x)∈[0,],x>2时,f(x)∈(,).
由,则f(x)有4个实根,
由题意,只要f(x)=a有2个实根,
则由图象可得当0<a≤时,f(x)=a有2个实根,
当a时,f(x)=a有2个实根.
综上可得:0<a≤或a.
故答案为:0<a≤或a..
【点睛】
本题考查函数的奇偶性和单调性的运用,考查方程和函数的转化思想,运用数形结合的思想方法是解决的常用方法.
17.(1)0(2)3
【解析】
【分析】
(1)根据终边相同的角同名三角函数值相等化简求值即可(2)先根据诱导公式化简,再利用同角三角函数间的关系化为正切即可.
【详解】
(1)
(2)
.
【点睛】
本题主要考查了三角函数的诱导公式,同名三角函数的基本关系,属于中档题.
18.(1) (2)
【解析】
【分析】
(1)根据,结合已知即可得,由此可得值, 根据是第三象限角,可知,即可求得的值.
(2)根据上述所得、的值可解得和的值,再代入求值即可.
【详解】
(1)
根据是第三象限角,可知
(2) 由上问求得:
故:得:
所以的值为.
【点睛】
本题主要考查三角函数的求值,解题关键是根据同角三角函数的关系对已知条件进行化简.
19.(1);(2);(3).
【解析】
【分析】
(1)将函数的解析式代入不等式,转化成关于对数不等式的求解问题;
(2)利用换元法,设将的值域转化为求二次函数的值域;
(3)利用对数恒等式将不等式转化为,利用配方法求得的值.
【详解】
(1)不等式,
因为,所以,
所以不等式的解集为:.
(2)当时,,令,
所以,
当时,,所以,
故函数的值域为.
(3)因为,
所以,即,解得:,
所以不等式的解集为.
【点睛】
本题考查对数不等式、对数函数的值域,考查函数与方程思想、转化与化归思想的灵活运用,考查运算求解能力,求解时注意换元法的运用,换元时要注意新元的取值范围.
20.(1); (2).
【解析】
【分析】
(1)首先时间时此人转过的角为,再根据时刻的高度,求函数的解析式;(2)根据(1)的结果,时,求的范围.
【详解】
(1)当时,此人相对于地面的高度.
在时间时此人转过的角为,
此时此人相对于地面的高度.
(2)由,得,不妨令,
则,即.
故在摩天轮转动的一圈内,此人相对于地面的高度不小于的时间为.
【点睛】
本题三角函数的实际应用问题,意在考查分析数据和抽象概括能力,属于中档题型.
21.(1)(2)(3)
【解析】
【分析】
(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值;
(2)恒成立需要保证即可,对二次函数进行分析,根据取到最大值时的情况得到的范围;
(3)通过条件将问题转化为二次函数在给定区间上有两个零点求的范围,这里将所有满足条件的不等式列出来,求解出的范围.
【详解】
解:(1)令,,则,对称轴为.
①,即,.
②,即,.
③,即,.
综上可知,
(2)由题意可知,,,的图象是开口向上的抛物线,最大值一定在端点处取得,所以有
故.
(3)令,.由题意可知,当时,有两个不等实数解,所以原题可转化为在内有两个不等实数根.所以有
【点睛】
(1)三角函数中,形如或者都可以采用换元法求解函数最值;
(2)讨论二次函数的零点的分布,最好可以采用数形结合的方法解决问题,这样很大程度上减少了遗漏条件的可能.
22.(1);
(2);
(3).
【解析】
【分析】
(1)根据表中数据可得关于的方程组,解出的值后可得的值,再由表中数据可得,从而可得函数的解析式.
(2)先求出的解析式,再求出的定义域,结合三角函数的单调性可得复合函数的单调增区间.
(3)令,设方程的根为,分①;②;③三种情况讨论在及上零点个数,再根据周期性得到的零点个数,结合题设条件可得的值及相应的零点个数.
【详解】
(1)根据表中的数据可得 ,解得,
故,所以,又,故.
所以.
(2)将函数的图像向右平移个单位,所得图像的解析式为:
,
再将所得图像上各点的横坐标缩小为原来的,纵坐标不变,得到函数的图像,
故.
此时,
令,则,故.
当时,为增函数,
故为减函数;
当时,为减函数;
故为增函数.
所以的增区间为.
(3),的周期为,
当时,令,考虑方程的根情况,
因,故在必有两个不同的实数根,
因为在有奇数个零点,故或.
若,则方程、在共有4个不同的实数根,
在有0个实数根或2个实数根,
故在有个根或个根,
与有奇数个零点矛盾,舍去.
若,则在共有2个不同的实数根,在有0个实数根或2个实数根,
故在有
个根或,
与有奇数个零点矛盾,舍去.
同理也不成立,所以或,
若,则,,
方程、在共有3个不同的实数根,而在上,有两个不同的根,无解,
所以在有个根,符合要求;
若,则,,
方程、在共有3个不同的实数根,而在上,无解,有一个根,
所以故在有个根,与题设矛盾,舍去.
综上,,在共有个不同的零点.
【点睛】
本题较为全面地考查了三角函数的图像和性质、三角函数的图像变换及复合函数零点的个数判断,注意与三角函数有关的复合函数的单调区间问题,要在定义域的基础上考虑其单调区间,而与三角函数有关的复合方程的零点个数问题,要结合函数的周期性来考虑,而一个周期上的函数零点判断,则需转化为内外两个方程的根的情况来讨论,本题属于难题.
试卷第2页,总3页
试卷第1页,总3页
时间:120分钟 分值:150分
1、选择题(本大题12小题,每题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案涂在答题卡上)
1.下列说法中不正确的是( )
A.与任意一个向量都平行
B.任何一个非零向量都可以平行移动
C.长度不相等而方向相反的两个向量一定是共线向量
D.两个有共同起点且共线的向量其终点必相同
2.( )
A. B. C. D.
3.若是直线上的一点,且,则当时,点的位置( )
A.在线段上 B.在线段的延长线上 C.在线段的延长线上 D.不能确定
4.下列函数中在上是增函数的是( )
A. B. C. D.
5.已知,,则的值为( ).
A. B. C. D.
6.已知,则( )
A. B. C. D.
7.函数的一个单调递增区间是
A. B. C. D.
8.函数,则不等式的解集为( )
A. B. C. D.
9.若,则的取值范围是( )
A. B.
C. D. (以上)
10.函数(且)的图像是下列图像中的( )
A. B.
C. D.
11.已知函数在区间上是增函数,其在区间上恰好取得一次最大值2,则的取值范围是( )
A. B. C. D.
12.已知函数(其中,,)的图像如图所示,将函数的图像向左平移个单位长度得到函数的图像,则关于函数的下列说法正确的是( )
① ② 的图像关于直线对称
③ ④在区间上单调递增
A.①② B.②③ C.③④ D.①④
二、填空题(本大题共4小题,每题5分,共20分,请把答案填在答卷相应位置。)
13.函数的值域为______。
14.要得到函数的图像,只需将的图像向左平移____ 个单位;
15.已知,关于的方程有两个不同的实数解,则实数的取值范围为______.
16.已知函数是定义域为的偶函数,当时,,若关于的方程有且仅有6个不同实数根,则实数的取值范围为______.
三、解答题(本大题共6题,共70分, 解答应写出文字说明、证明过程或演算步骤.)
17.(1)计算;
(2)已知,求的值.
18.已知是第三象限角,且.
(1)求的值;
(2)求的值.
19.已知函数(且),(且)
(1)当时,求关于的不等式的解集;
(2)当时,求的值域;
(3)求关于的不等式的解集;
20.如图,一个摩天轮的半径为,轮子的最低处距离地面.如果此摩天轮按逆时针匀速转动,每转一圈,且当摩天轮上某人经过点(点与摩天轮中心的高度相同)时开始计时.
(1)求此人相对于地面的高度(单位:)关于时间(单位:)的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不小于?
21.设函数(R).
(1)若不等式在上恒成立,求的取值范围;
(2)若方程在上有四个不相等的实数根,求的取值范围.
22.某同学用“五点法”画函数在某一周期内的图像时,列表并填入的部分数据如下表:
0
0 1 0 0
0 0 0
(1)请写出上表的函数的解析式;
(2)将函数的图像向右平移个单位,再将所得图像上各点的横坐标缩小为原来的,纵坐标不变,得到函数的图像,求的解析式及的单调递增区间;
(3)在(2)的条件下,若在上恰有奇数个零点,求实数与零点个数的值.
江苏名扬教育高一年级秋学期第二次月考数学试卷参考答案
1.D
【解析】
【分析】
通过零向量的概念判断A;
通过向量的概念判断B;
通过共线向量的定义判断C;
通过共线向量的定义判断D.
【详解】
的方向是任意的,和任意向量都平行,故A正确;
向量的是既有大小又有方向的量,任意移动还是原向量,故B正确;
共线向量是方向相同或相反的向量,故C正确;
起点相同的共线向量可以是方向相反的向量,终点不一定相同,故D错误,
故选:D.
【点睛】
本题考查向量的方向问题,是基础题.
2.A
【解析】
【分析】
根据诱导公式:化简,即可得到答案.
【详解】
故选:A.
【点睛】
本考查了由诱导公式求三角函数值,能熟练使用诱导公式是解本题关键.
3.C
【解析】
【分析】
根据题意易知点不可能与,重合,故而可分为在线段上,在线段的延长线上和在线段的延长线上三种情形逐一分析即可.
【详解】
根据题意易知点不可能与,重合,
当在线段上时,;
当在线段的延长线上时,;
当在线段的延长线上时,;
故选:C.
【点睛】
本题主要考查定比分点分有向线段成的比的定义,把它转化为线段的长度比的相反数,数形结合是解题的关键,属于中档题.
4.D
【解析】
【分析】
分别根据函数的单调性进行判定即可得到结论.
【详解】
对于A选项:在上是减函数,不满足条件.
对于B选项:在上是减函数,不满足条件.
对于C选项:,令t=2x,当时,此时y=sint在上不单调,不满足条件.
对于D选项:,当时,此时y=cost在上是增函数,满足条件.
故选D.
【点睛】
本题主要考查三角函数的单调性,要求熟练掌握三角函数的图象.
5.B
【解析】
【分析】
利用同角三角函数的基本关系,求得的值.
【详解】
因为,解得:或,
因为,所以.
故选:B.
【点睛】
本题考查同角三角函数的基本关系,考查基本运算求解能力,求解时注意考虑的取值范围,防止出现符号错误.
6.D
【解析】
【分析】
观察可知,,则由诱导公式可求得
【详解】
∵,
故选:D.
【点睛】
本题考查诱导公式的用法,属于基础题
7.A
【解析】
【分析】
首先由诱导公式对函数的解析式进行恒等变形,然后求解其单调区间即可.
【详解】
函数的解析式即:,
其单调增区间满足:,
解得:,
令可得函数的一个单调递增区间为.
故选:A.
【点睛】
本题主要考查诱导公式的应用,三角函数单调区间的求解等知识,意在考查学生的转化能力和计算求解能力.
8.A
【解析】
【分析】
先根据分段函数转化为两个不等式组,解得结果.
【详解】
因为,所以或
因此或,或,即
故选:A
【点睛】
本题考查分段函数性质以及解指对数不等式,考查基本分析求解能力,属中档题.
9.D
【解析】
【分析】
根据,左边式子上下分之,分母分别乘,,所以cosx<0,解出x的取值范围即可
【详解】
因为,
所以,
所以cosx<0,解得: (以上),故选:D
【点睛】
本题主要化简三角函数等式,求解x取值范围
10.C
【解析】
【分析】
将函数表示为分段函数的形式,由此确定函数图像.
【详解】
依题意,.由此判断出正确的选项为C.
故选C.
【点睛】
本小题主要考查三角函数图像的识别,考查分段函数解析式的求法,考查同角三角函数的基本关系式,属于基础题.
11.A
【解析】
【分析】
根据函数的单调性得到,又因为在区间上恰好取得一次最大值,进而得到两者取交集即可.
【详解】
函数 在区间上是增函数,
故得到
当时,,函数在区间上恰好取得一次最大值,故得到
综上:
故答案为:A.
【点睛】
这个题目考查了三角函数的单调性的应用以及三角函数最值的求法,属于基础题. 在研究函数的单调性和最值时,一般采用的是整体思想,将ω x +φ看做一个整体,地位等同于sinx中的x.
12.B
【解析】
【分析】
根据图像得到表达式,再利用平移得到表达式,依次判断四个选项的正误,得到答案.
【详解】
函数(其中,,)
根据图像知:
将函数的图像向左平移个单位长度得到函数的图像
故①错误③正确
时是对称轴,②正确
在区间上先增后减,④错误
故答案选B
【点睛】
本题考查了根据图像求三角函数表达式,三角函数的平移,三角函数的对称抽和单调性,考查知识点较多,意在锻炼学生的综合应用能力.
13.
【解析】
【分析】
根据三角函数值在各象限的符号,讨论去掉绝对值,即可求出.
【详解】
由题意可知,角的终边不可能在坐标轴上,所以分四类:
当角的终边在第一象限,则,所以;
当角的终边在第二象限,则,所以;
当角的终边在第三象限,则,所以;
当角的终边在第四象限,则,所以;
故答案为:.
【点睛】
本题主要考查三角函数值在各象限的符号.
14.
【解析】
【分析】
由条件利用诱导公式,函数的图像变化规律,可得结论.
【详解】
将函数的图像上所有点向左平移个单位纵坐标不变,可得函数的图像.
故答案为:
【点睛】
本题主要考查诱导公式的应用、函数的图像变化规律,属于基础题.
15.
【解析】
【分析】
在同一坐标中,做出函数,,的图象,利用数形结合根据交点个数即可求解
【详解】
令,,,作出的图象如图所示.若
在上有两个不同的实数解,则与应有两个不同的交点,所以.
答案:
【点睛】
本题主要考查了函数与方程,正弦型函数图象,数形结合的思想方法,属于中档题.
16.0<a≤或a.
【解析】
【分析】
运用偶函数的性质,作出函数f(x)的图象,由5[f(x)]2﹣(5a+4)f(x)+4a=0,解得f(x)=a或f(x),结合图象,分析有且仅有6个不同实数根的a的情况,即可得到a的范围.
【详解】
函数是定义域为的偶函数,作出函数f(x)的图象如图:
关于x的方程5[f(x)]2﹣(5a+4)f(x)+4a=0,
解得f(x)=a或f(x),
当0≤x≤2时,f(x)∈[0,],x>2时,f(x)∈(,).
由,则f(x)有4个实根,
由题意,只要f(x)=a有2个实根,
则由图象可得当0<a≤时,f(x)=a有2个实根,
当a时,f(x)=a有2个实根.
综上可得:0<a≤或a.
故答案为:0<a≤或a..
【点睛】
本题考查函数的奇偶性和单调性的运用,考查方程和函数的转化思想,运用数形结合的思想方法是解决的常用方法.
17.(1)0(2)3
【解析】
【分析】
(1)根据终边相同的角同名三角函数值相等化简求值即可(2)先根据诱导公式化简,再利用同角三角函数间的关系化为正切即可.
【详解】
(1)
(2)
.
【点睛】
本题主要考查了三角函数的诱导公式,同名三角函数的基本关系,属于中档题.
18.(1) (2)
【解析】
【分析】
(1)根据,结合已知即可得,由此可得值, 根据是第三象限角,可知,即可求得的值.
(2)根据上述所得、的值可解得和的值,再代入求值即可.
【详解】
(1)
根据是第三象限角,可知
(2) 由上问求得:
故:得:
所以的值为.
【点睛】
本题主要考查三角函数的求值,解题关键是根据同角三角函数的关系对已知条件进行化简.
19.(1);(2);(3).
【解析】
【分析】
(1)将函数的解析式代入不等式,转化成关于对数不等式的求解问题;
(2)利用换元法,设将的值域转化为求二次函数的值域;
(3)利用对数恒等式将不等式转化为,利用配方法求得的值.
【详解】
(1)不等式,
因为,所以,
所以不等式的解集为:.
(2)当时,,令,
所以,
当时,,所以,
故函数的值域为.
(3)因为,
所以,即,解得:,
所以不等式的解集为.
【点睛】
本题考查对数不等式、对数函数的值域,考查函数与方程思想、转化与化归思想的灵活运用,考查运算求解能力,求解时注意换元法的运用,换元时要注意新元的取值范围.
20.(1); (2).
【解析】
【分析】
(1)首先时间时此人转过的角为,再根据时刻的高度,求函数的解析式;(2)根据(1)的结果,时,求的范围.
【详解】
(1)当时,此人相对于地面的高度.
在时间时此人转过的角为,
此时此人相对于地面的高度.
(2)由,得,不妨令,
则,即.
故在摩天轮转动的一圈内,此人相对于地面的高度不小于的时间为.
【点睛】
本题三角函数的实际应用问题,意在考查分析数据和抽象概括能力,属于中档题型.
21.(1)(2)(3)
【解析】
【分析】
(1)通过换元法将函数变形为二次函数,同时利用分类讨论的方法求解最大值;
(2)恒成立需要保证即可,对二次函数进行分析,根据取到最大值时的情况得到的范围;
(3)通过条件将问题转化为二次函数在给定区间上有两个零点求的范围,这里将所有满足条件的不等式列出来,求解出的范围.
【详解】
解:(1)令,,则,对称轴为.
①,即,.
②,即,.
③,即,.
综上可知,
(2)由题意可知,,,的图象是开口向上的抛物线,最大值一定在端点处取得,所以有
故.
(3)令,.由题意可知,当时,有两个不等实数解,所以原题可转化为在内有两个不等实数根.所以有
【点睛】
(1)三角函数中,形如或者都可以采用换元法求解函数最值;
(2)讨论二次函数的零点的分布,最好可以采用数形结合的方法解决问题,这样很大程度上减少了遗漏条件的可能.
22.(1);
(2);
(3).
【解析】
【分析】
(1)根据表中数据可得关于的方程组,解出的值后可得的值,再由表中数据可得,从而可得函数的解析式.
(2)先求出的解析式,再求出的定义域,结合三角函数的单调性可得复合函数的单调增区间.
(3)令,设方程的根为,分①;②;③三种情况讨论在及上零点个数,再根据周期性得到的零点个数,结合题设条件可得的值及相应的零点个数.
【详解】
(1)根据表中的数据可得 ,解得,
故,所以,又,故.
所以.
(2)将函数的图像向右平移个单位,所得图像的解析式为:
,
再将所得图像上各点的横坐标缩小为原来的,纵坐标不变,得到函数的图像,
故.
此时,
令,则,故.
当时,为增函数,
故为减函数;
当时,为减函数;
故为增函数.
所以的增区间为.
(3),的周期为,
当时,令,考虑方程的根情况,
因,故在必有两个不同的实数根,
因为在有奇数个零点,故或.
若,则方程、在共有4个不同的实数根,
在有0个实数根或2个实数根,
故在有个根或个根,
与有奇数个零点矛盾,舍去.
若,则在共有2个不同的实数根,在有0个实数根或2个实数根,
故在有
个根或,
与有奇数个零点矛盾,舍去.
同理也不成立,所以或,
若,则,,
方程、在共有3个不同的实数根,而在上,有两个不同的根,无解,
所以在有个根,符合要求;
若,则,,
方程、在共有3个不同的实数根,而在上,无解,有一个根,
所以故在有个根,与题设矛盾,舍去.
综上,,在共有个不同的零点.
【点睛】
本题较为全面地考查了三角函数的图像和性质、三角函数的图像变换及复合函数零点的个数判断,注意与三角函数有关的复合函数的单调区间问题,要在定义域的基础上考虑其单调区间,而与三角函数有关的复合方程的零点个数问题,要结合函数的周期性来考虑,而一个周期上的函数零点判断,则需转化为内外两个方程的根的情况来讨论,本题属于难题.
试卷第2页,总3页
试卷第1页,总3页
同课章节目录
