人教版八年级数学下册课件20.1.1 平均数(2课时34张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件20.1.1 平均数(2课时34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览








文档简介
课件34张PPT。教学课件
数学 八年级下册 人教版
第二十章 数据的分析
20.1.1 平均数
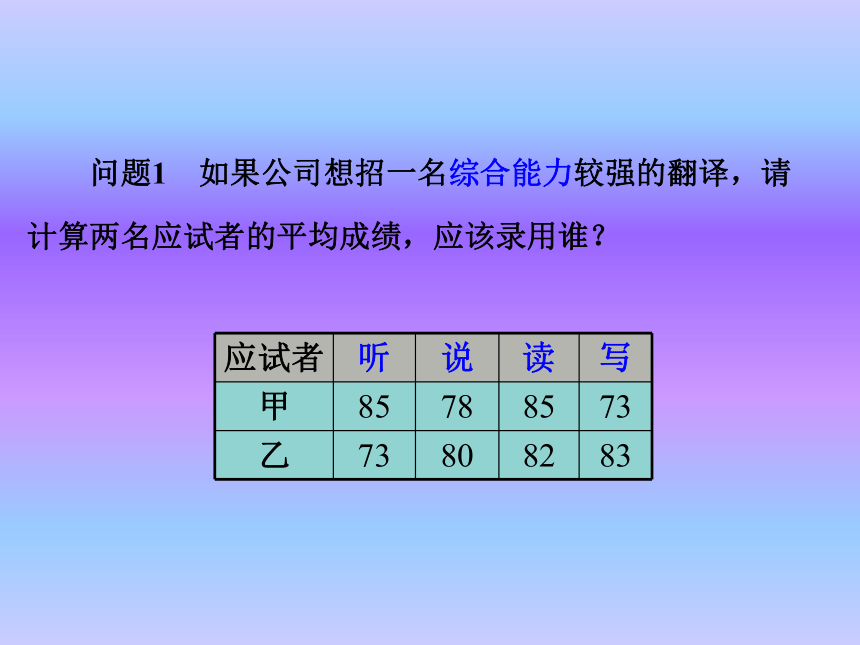
第1课时 农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块试验田进行试验,得到各试验田每公顷的产量如下表。根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢?探究:某市三个郊县的人数及人均耕地面积如下表.这个市郊县人均耕地面积是多少(精确到0.01公顷)?小明求得这个市郊县的人均耕地面积为:你认为小明的做法有道理吗?为什么? 小明求得这个市郊县的人均耕地面积为: 你认为小明的做法有道理吗?为什么? 由于各郊县的人数不同,各郊县的人均耕地面积对这个市郊县的人均耕地面积的影响不同,因此这个市郊县的人均耕地面积不能是三个郊县人均耕地面积的算术平均数,而应该是:0.15×15表示A县耕地面积吗?你能说出这个式子中分子,分母各表示什么吗?叫做这n个数的加权平均数。数据的权能够反映的数据的相对“重要程度”。 上面的平均数0.17称为3个数0.15、0.21、0.18的加权平均数(weighted average),三个郊县的人数(单位是万),15、7、10分别为三个数据的权(weight). 问题1 如果公司想招一名综合能力较强的翻译,请
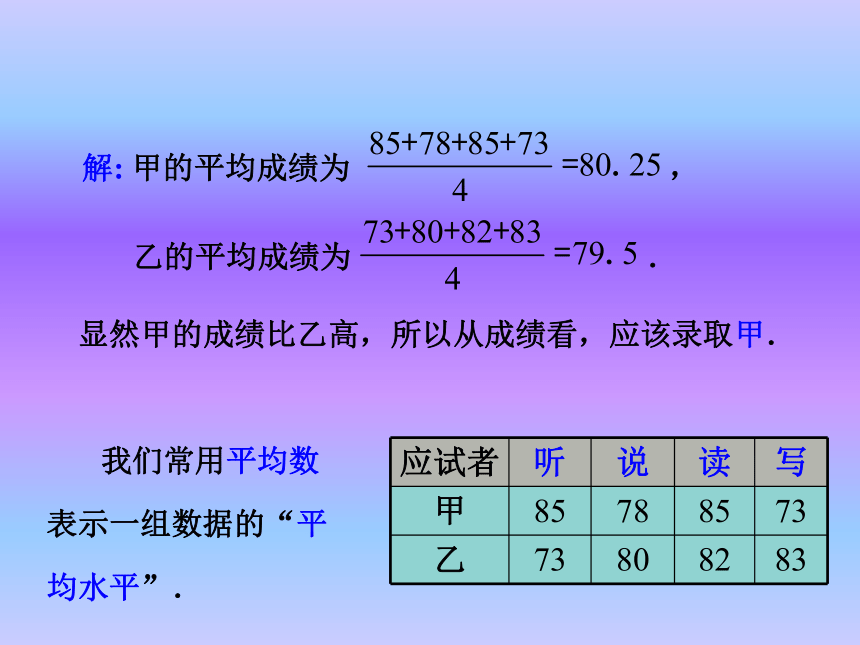
计算两名应试者的平均成绩,应该录用谁? 显然甲的成绩比乙高,所以从成绩看,应该录取甲.
我们常用平均数
表示一组数据的“平
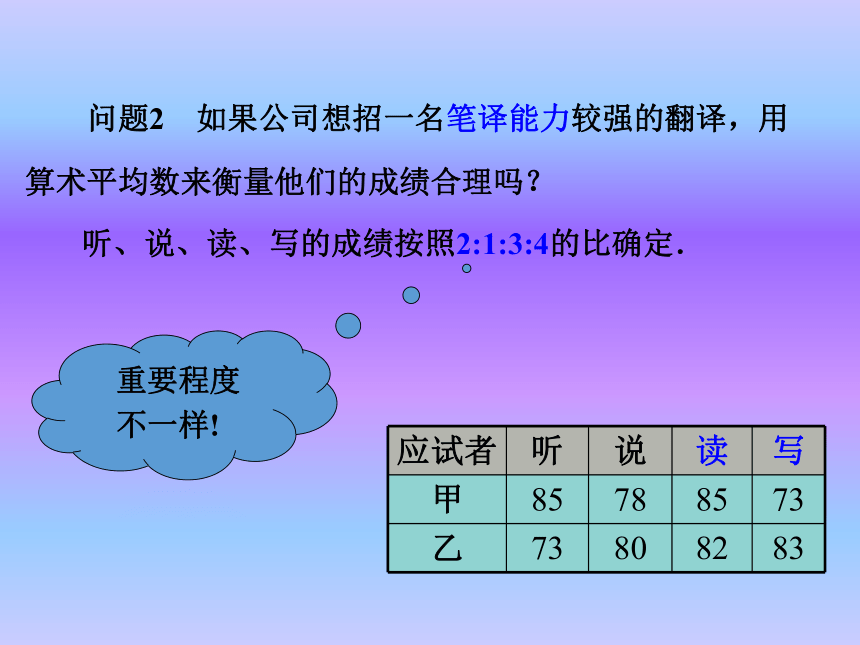
均水平”. 问题2 如果公司想招一名笔译能力较强的翻译,用
算术平均数来衡量他们的成绩合理吗? 听、说、读、写的成绩按照2:1:3:4的比确定. 因为乙的成绩比甲高,所以应该录取乙.思考 能把这种加权平均数的计算方法推广到一般吗? 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
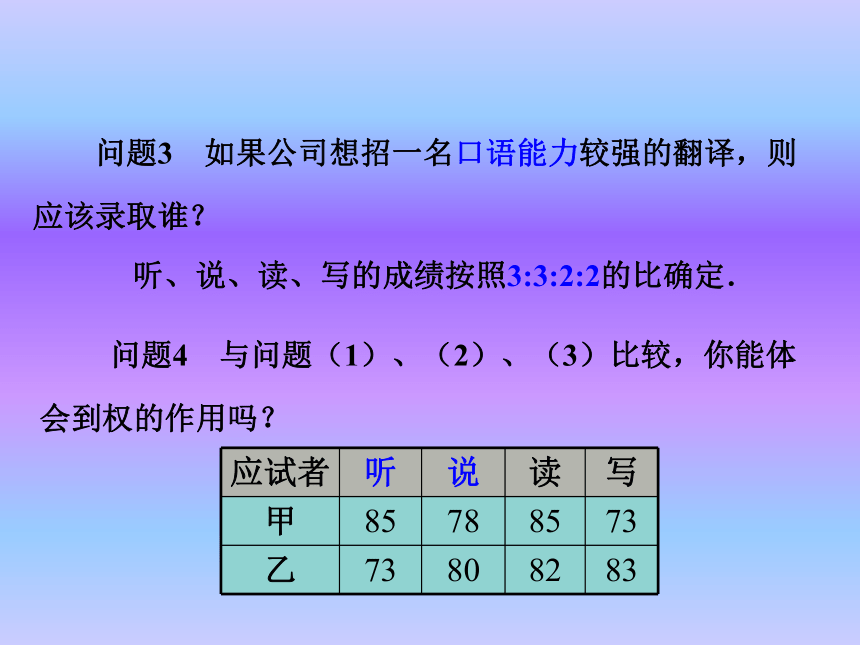
叫做这n个数的加权平均数. 问题4 与问题(1)、(2)、(3)比较,你能体
会到权的作用吗? 问题3 如果公司想招一名口语能力较强的翻译,则
应该录取谁? 听、说、读、写的成绩按照3:3:2:2的比确定. 例1. 某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?甲乙甲解:根据题意,求甲、乙各项成绩的平均数,得:答:因为___的平均成绩比_____高,所以___将被录取.(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?解:根据题意,求甲、乙各项成绩的加权平均数,得 :答:因为_____>_____,所以_____将被录取.乙 例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如表所示,请确定两人的名次.注:本题中演讲内容、演讲能力、演讲效果三项成绩的权分别是 _______、________、________ 50% 40% 10%解:选手A的最后得分是:
选手B的最后得分是:答:由上可知选手____获得第一名,选手____
获得第二名.BA(1)加权平均数在数据分析中的作用是什么?
当一组数据中各个数据重要程度不同时,加权平
均数能更好地反映这组数据的平均水平.
(2)权的作用是什么?
权反映数据的重要程度,数据权的改变一般会影
响这组数据的平均水平.第二十章 数据的分析
20.1.1 平均数
第2课时1、如何求一组数据的平均数?
2、七位裁判给某体操运动员打的分数分别为:7.8,8.1,9.5,7.4,8.4,6.4,8.3.如果去掉一个最高分,去掉一个最低分,那么,这位运动员平均得分是多少?
3.晨光中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次是95、90、85.小桐这学期的体育成绩是多少?学习目标:
1.理解算术平均数的简便算法与加权平均数的一致性,会用计算器求加权平均数;
2.会根据频数分布计算加权平均数,理解它所体现的统计意义,发展数据分析能力.
3. 会根据样本平均数估计数据总体的集中趋势,进一步体会用样本估计总体的思想.
学习重点:
根据频数分布求加权平均数的近似值. 问题1 某跳水队有5个运动员,他们的身高(单
位:cm)分别为156,158,160,162,170.试求他们
的平均身高. 解:他们的平均身高为:所以他们的平均身高为161.2 cm. 问题2 某班级为了解同学年龄情况,作了一次年
龄调查,结果如下:13岁8人,14岁16人,15岁24人,
16岁2人.求这个班级学生的平均年龄(结果取整数). 解:这个班级学生的平均年龄为: 所以他们的平均年龄约为14岁. 在求 n 个数的算术平均数时,如果 x1 出现 f1 次, x2
出现 f2 次,…,xk 出现 fk 次(这里 f1 + f2 +…+ fk = n ),
那么这 n 个数的平均数
也叫做 x1 ,x2 ,…,xk 这 k个数的加权平均数,其中f1 ,
f2 ,…,fk 分别叫做x1 ,x2 ,…,xk 的权. 这种求平均数的方法与上一节课中的加权平均数求法有什么相同之处? 说明 根据频数分布表求加权平均数时,统计中
常用各组的组中值代表各组的实际数据,把各组的频数
看作相应组中值的权. 根据上面的频数分布表求加权平均数时,统计中常用的各组的组中值代表各组的实际数据,把各组频数看作相应组中值的权。例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3,由此这天5路公共汽车平均每班的载客量是: 从表中,你能知道这一天5路公共汽车大约有多少班次的载客量在平均载客量以上吗?占全天总班次的百分比是多少? 由表格可知, 81≤x<101的18个班次 和101≤x<121的15个班次共有33个班次超过平均载客量,占全天总班次的百分比为33/83等于39.8% 问题3 果园里有100 棵梨树,在收获前,果农常
会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量? 所以平均每棵梨树上梨的个数为154. (1)果农从100 棵梨树中任意选出10 棵,数出这10
棵梨树上梨的个数,得到以下数据:154,150,155,
155,159,150,152,155,153,157.你能估计出平均
每棵树的梨的个数吗? (2)果农从这10 棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表: 能估计出这批梨的平均质量吗? 所以平均每个梨的质量约为0.42 kg.用样本估计总体;
用样本平均数估计总体平均数.(3)能估计出该果园中梨的总产量吗? 思考 这个生活中的问题是如何解决的,体现了怎样的统计思想?所以该果园中梨的总产量约为6 468 kg. 例1 为了解全班学生做课外作业所用时间的情况,
老师对学生做课外作业所用时间进行调查,统计情况如
下表,求该班学生平均每天做课外作业所用时间(结果
取整数,可使用计算器). 例2 某灯泡厂为了测量一批灯泡的使用寿命,从中
随机抽查了50只灯泡,它们的使用寿命如下表所示.这
批灯泡的平均使用寿命是多少? 解:据上表得各小组的组中值,于是 (1)当一组数据中有多个数据重复出现时,如何简便
地反映这组数据的集中趋势?
利用加权平均数.
(2)据频数分布求加权平均数时,你如何确定数据与
相应的权?试举例说明.
(3)在抽样调查得到样本数据后,你如何处理样本
数据并估计总体数据的集中趋势?
样本平均数估计总体平均数.
数学 八年级下册 人教版
第二十章 数据的分析
20.1.1 平均数
第1课时 农科院为了选出适合某地种植的甜玉米种子,对甲、乙两个品种各用10块试验田进行试验,得到各试验田每公顷的产量如下表。根据这些数据,应为农科院选择甜玉米种子提出怎样的建议呢?探究:某市三个郊县的人数及人均耕地面积如下表.这个市郊县人均耕地面积是多少(精确到0.01公顷)?小明求得这个市郊县的人均耕地面积为:你认为小明的做法有道理吗?为什么? 小明求得这个市郊县的人均耕地面积为: 你认为小明的做法有道理吗?为什么? 由于各郊县的人数不同,各郊县的人均耕地面积对这个市郊县的人均耕地面积的影响不同,因此这个市郊县的人均耕地面积不能是三个郊县人均耕地面积的算术平均数,而应该是:0.15×15表示A县耕地面积吗?你能说出这个式子中分子,分母各表示什么吗?叫做这n个数的加权平均数。数据的权能够反映的数据的相对“重要程度”。 上面的平均数0.17称为3个数0.15、0.21、0.18的加权平均数(weighted average),三个郊县的人数(单位是万),15、7、10分别为三个数据的权(weight). 问题1 如果公司想招一名综合能力较强的翻译,请
计算两名应试者的平均成绩,应该录用谁? 显然甲的成绩比乙高,所以从成绩看,应该录取甲.
我们常用平均数
表示一组数据的“平
均水平”. 问题2 如果公司想招一名笔译能力较强的翻译,用
算术平均数来衡量他们的成绩合理吗? 听、说、读、写的成绩按照2:1:3:4的比确定. 因为乙的成绩比甲高,所以应该录取乙.思考 能把这种加权平均数的计算方法推广到一般吗? 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
叫做这n个数的加权平均数. 问题4 与问题(1)、(2)、(3)比较,你能体
会到权的作用吗? 问题3 如果公司想招一名口语能力较强的翻译,则
应该录取谁? 听、说、读、写的成绩按照3:3:2:2的比确定. 例1. 某公司欲招聘一名公关人员.对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如下表所示.(1)如果公司认为面试和笔试成绩同等重要,从他们的成绩看,谁将被录取?甲乙甲解:根据题意,求甲、乙各项成绩的平均数,得:答:因为___的平均成绩比_____高,所以___将被录取.(2)如果公司认为,作为公关人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?解:根据题意,求甲、乙各项成绩的加权平均数,得 :答:因为_____>_____,所以_____将被录取.乙 例2 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如表所示,请确定两人的名次.注:本题中演讲内容、演讲能力、演讲效果三项成绩的权分别是 _______、________、________ 50% 40% 10%解:选手A的最后得分是:
选手B的最后得分是:答:由上可知选手____获得第一名,选手____
获得第二名.BA(1)加权平均数在数据分析中的作用是什么?
当一组数据中各个数据重要程度不同时,加权平
均数能更好地反映这组数据的平均水平.
(2)权的作用是什么?
权反映数据的重要程度,数据权的改变一般会影
响这组数据的平均水平.第二十章 数据的分析
20.1.1 平均数
第2课时1、如何求一组数据的平均数?
2、七位裁判给某体操运动员打的分数分别为:7.8,8.1,9.5,7.4,8.4,6.4,8.3.如果去掉一个最高分,去掉一个最低分,那么,这位运动员平均得分是多少?
3.晨光中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次是95、90、85.小桐这学期的体育成绩是多少?学习目标:
1.理解算术平均数的简便算法与加权平均数的一致性,会用计算器求加权平均数;
2.会根据频数分布计算加权平均数,理解它所体现的统计意义,发展数据分析能力.
3. 会根据样本平均数估计数据总体的集中趋势,进一步体会用样本估计总体的思想.
学习重点:
根据频数分布求加权平均数的近似值. 问题1 某跳水队有5个运动员,他们的身高(单
位:cm)分别为156,158,160,162,170.试求他们
的平均身高. 解:他们的平均身高为:所以他们的平均身高为161.2 cm. 问题2 某班级为了解同学年龄情况,作了一次年
龄调查,结果如下:13岁8人,14岁16人,15岁24人,
16岁2人.求这个班级学生的平均年龄(结果取整数). 解:这个班级学生的平均年龄为: 所以他们的平均年龄约为14岁. 在求 n 个数的算术平均数时,如果 x1 出现 f1 次, x2
出现 f2 次,…,xk 出现 fk 次(这里 f1 + f2 +…+ fk = n ),
那么这 n 个数的平均数
也叫做 x1 ,x2 ,…,xk 这 k个数的加权平均数,其中f1 ,
f2 ,…,fk 分别叫做x1 ,x2 ,…,xk 的权. 这种求平均数的方法与上一节课中的加权平均数求法有什么相同之处? 说明 根据频数分布表求加权平均数时,统计中
常用各组的组中值代表各组的实际数据,把各组的频数
看作相应组中值的权. 根据上面的频数分布表求加权平均数时,统计中常用的各组的组中值代表各组的实际数据,把各组频数看作相应组中值的权。例如在1≤x<21之间的载客量近似地看作组中值11,组中值11的权是它的频数3,由此这天5路公共汽车平均每班的载客量是: 从表中,你能知道这一天5路公共汽车大约有多少班次的载客量在平均载客量以上吗?占全天总班次的百分比是多少? 由表格可知, 81≤x<101的18个班次 和101≤x<121的15个班次共有33个班次超过平均载客量,占全天总班次的百分比为33/83等于39.8% 问题3 果园里有100 棵梨树,在收获前,果农常
会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量? 所以平均每棵梨树上梨的个数为154. (1)果农从100 棵梨树中任意选出10 棵,数出这10
棵梨树上梨的个数,得到以下数据:154,150,155,
155,159,150,152,155,153,157.你能估计出平均
每棵树的梨的个数吗? (2)果农从这10 棵梨树的每一棵树上分别随机摘4
个梨,这些梨的质量分布如下表: 能估计出这批梨的平均质量吗? 所以平均每个梨的质量约为0.42 kg.用样本估计总体;
用样本平均数估计总体平均数.(3)能估计出该果园中梨的总产量吗? 思考 这个生活中的问题是如何解决的,体现了怎样的统计思想?所以该果园中梨的总产量约为6 468 kg. 例1 为了解全班学生做课外作业所用时间的情况,
老师对学生做课外作业所用时间进行调查,统计情况如
下表,求该班学生平均每天做课外作业所用时间(结果
取整数,可使用计算器). 例2 某灯泡厂为了测量一批灯泡的使用寿命,从中
随机抽查了50只灯泡,它们的使用寿命如下表所示.这
批灯泡的平均使用寿命是多少? 解:据上表得各小组的组中值,于是 (1)当一组数据中有多个数据重复出现时,如何简便
地反映这组数据的集中趋势?
利用加权平均数.
(2)据频数分布求加权平均数时,你如何确定数据与
相应的权?试举例说明.
(3)在抽样调查得到样本数据后,你如何处理样本
数据并估计总体数据的集中趋势?
样本平均数估计总体平均数.
