高中数学人教版必修1课件:3.1.1方程的根与函数的零点(共28张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:3.1.1方程的根与函数的零点(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 902.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 10:39:56 | ||
图片预览







文档简介
(共28张PPT)
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,
日用之繁,无处不用数学。
--------华罗庚
3.1.1
《方程的根与函数的零点》
重点:
方程的根与函数的零点的关系。
难点:
判断函数零点的个数问题。
了解零点的概念,理解方程的根与零点的关系,会判断函数零点的所在区间。
教学目 标
自主学习 :阅读p86~88, 理解下列问题:
1. 函数零点的概念?
2. 函数零点与方程的根有什么关系?
3. 怎样判断函数在某区间上存在零点?
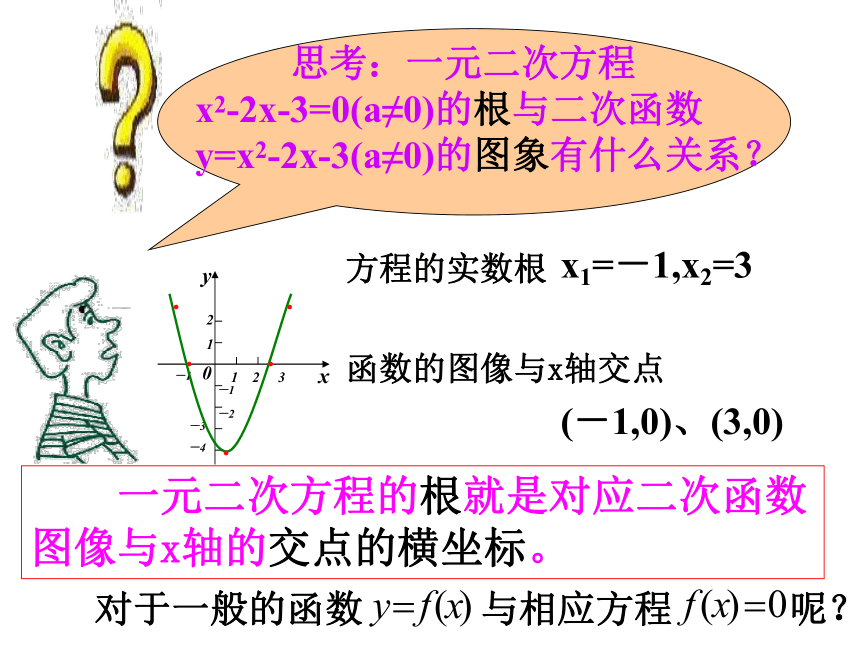
对于一般的函数 与相应方程 呢?
一元二次方程的根就是对应二次函数图像与x轴的交点的横坐标。
方程的实数根
x1=-1,x2=3
函数的图像与x轴交点
(-1,0)、(3,0)
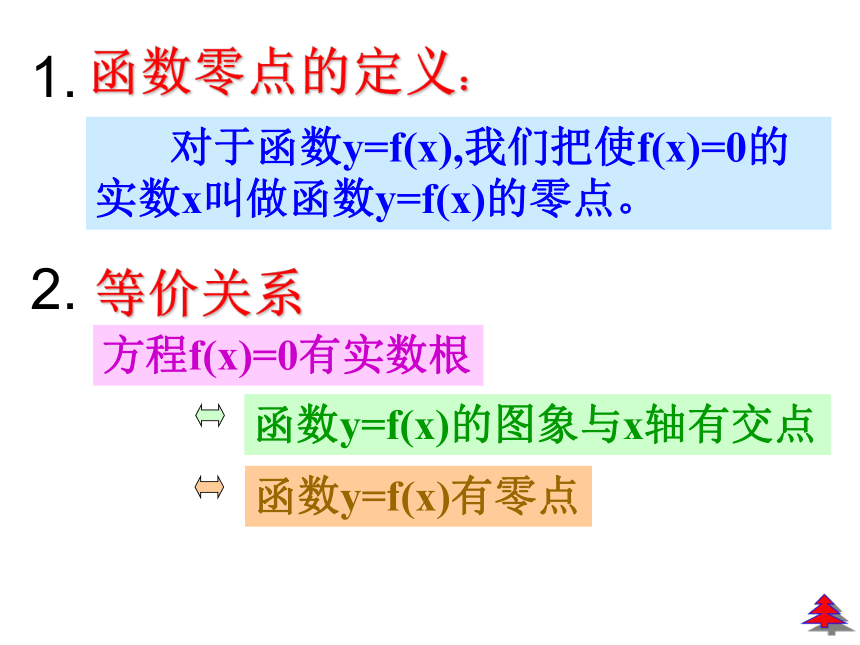
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
方程f(x)=0有实数根
函数零点的定义:
等价关系
1.
2.
1
0个
1个
巩固训练 :
有
有
<
<
3. 如何判断函数在某个区间内有无零点
合作交流 :
猜想:若函数在区间[a,b]上图象是连续的,如果有 成立,那么函数区间(a,b)上有零点。
f(a)·f(b)< 0
有
<
有
<
有
<
如果函数
的一条曲线,并且 ,
(a,b)内有零点,即存在
3. 零点存在性定理:
连续不断
那么
c也就是方程
f(a)·f(b)<0
(1)f(a)·f(b)<0则函数y=f(x)在区间(a,b)内有零点。
(2) 函数y=f(x)在区间(a,b)内有零点f(a)·f(b)<0。
(3) f(a)·f(b)<0 函数y=f(x)在区间(a,b)内只有一个零点。
注意:
1 函数是连续的。
定理辨析:
错
错
错
2 定理不可逆。
3 至少存在一个零点。
2.已知函数f(x)的图象是连续不断的,有如下对应值表:
??
那么函数在区间[1,6]上的零点至少有(? )个?
?A.5个?????? B.4个??? ??? C.3个?????? D.2个
C
巩固训练
1. f(x)=x3+x-1在下列哪个区间上有零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
B
x 1 2 3 4 5 6 7
f(x) 23 9 -7 11 -5 -12 -26
3.方程 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解法二:
三、求函数零点或零点个数的方法:
(1)定义法:解方程 f(x)=0,
得出函数的零点。
(3)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。
(2)定理法:函数零点存在性定理。
观察如上三个函数图像
思考:函数要满足什么条件在区间[a,b]上至多只有一个有零点?
函数在区间[a,b]上是单调连续的,则函数在区间[a,b]至多只有一个零点。
探究2:
0
0
0
a
b
y
x
y
x
y
x
一元二次方程的根及其相应
二次函数的图象与x轴交点的关系;
函数零点的概念;
函数零点与方程的根的关系;
函数零点存在性定理.
小结
布置作业:
P92 习题3.1 第2题
随堂检测
1.函数f(x)=x(x2-16)的零点为( ? )
A. (0,0),(4,0)?? ?? B.0,4????
C. (–4,0),(0,0),(4,0)??? D.–4,0,4
D
3.已知函数f(x)是定义域为R的奇函数,且f(x)在(0,+∞)上有一个零点,则f(x)的零点个数为(?? )
A.3????? B.2???? C.1???? D.不确定
A
4.若函数 仅有一个零点,求实数a的取值范围。
练习:
1.利用函数图象判断下列方程有没有根,有几个根:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
2.利用函数的图象,指出下列函数零点所在的大致区间:
(1)f(x)= -x3-3x+5;
(2)f(x)=2x · ln(x-2)-3;
(3)f(x)=ex-1+4x-4;
(4)f(x)=3(x+2)(x-3)(x+4)+x.
有
没有
有
没有
有
没有
有
没有
1(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下:
它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。
(1) -x2+3x+5=0
1(2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x+3 , 作出函数f(x)的图象,如下:
它与x轴没有交点,所以方程2x(x-2)=-3无实数根。
(2) 2x(x-2)=-3
1(3)解:x2 =4x-4可化为x2-4x+4 =0,令f(x)= x2-4x+4,作出
函数f(x)的图象,如下:
它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。
(3) x2 =4x-4
1(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)= 2x2 +2x-5, 作出函数f(x)的图象,
如下:
它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。
(4) 5 x2 +2x=3 x2 +5
2(1)解:作出函数的图象,如下:
因为f(1)=1>0,f(1.5)=-2.875<0,
所以f(x)= -x3-3x+5在区间(1, 1.5)
上有零点。又因为f(x)是(-∞,+∞)
上的减函数,所以在区间(1, 1.5)上有
且只有一个零点。
2(1) f(x)= -x3-3x+5
2(2)解:作出函数的图象,如下:
因为f(3)=-3<0,f(4)≈2.545>0,所以f(x)=
2x · ln(x-2)-3在区间(3,4)上有零点。又因为
f(x) =2x · ln(x-2)-3是(2,+∞)上的增函数,
所以在区间(3,4)上有且只有一个零点。
2(2) f(x)=2x · ln(x-2)-3
2(3)解:作出函数的图象,如下:
因为f(0)≈-3.63<0,f(1)
=1>0,所以f(x)= ex-1+4x-4
在区间(0,1)上有零点。又因
为f(x) = ex-1+4x-4是(-∞ ,
+∞)上的增函数,所以在
区间(0,1)上有且只有一个零
点。
2(3) f(x)=ex-1+4x-4
2(4)解:作出函数的图象,如下:
因为f(-4)=-4<0,f(- 3)=15>0,
f(-2)=-2<0,f(2)=-70<0, f(3)=3>0,
所以f(x)= 3(x+2)(x - 3)(x+4)+x 在区间
(-4,-3 )、 (-3,-2,)、 (2,3 )上各有
一个零点。
2(4) f(x)=3(x+2)(x-3)(x+4)+x
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,
日用之繁,无处不用数学。
--------华罗庚
3.1.1
《方程的根与函数的零点》
重点:
方程的根与函数的零点的关系。
难点:
判断函数零点的个数问题。
了解零点的概念,理解方程的根与零点的关系,会判断函数零点的所在区间。
教学目 标
自主学习 :阅读p86~88, 理解下列问题:
1. 函数零点的概念?
2. 函数零点与方程的根有什么关系?
3. 怎样判断函数在某区间上存在零点?
对于一般的函数 与相应方程 呢?
一元二次方程的根就是对应二次函数图像与x轴的交点的横坐标。
方程的实数根
x1=-1,x2=3
函数的图像与x轴交点
(-1,0)、(3,0)
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。
方程f(x)=0有实数根
函数零点的定义:
等价关系
1.
2.
1
0个
1个
巩固训练 :
有
有
<
<
3. 如何判断函数在某个区间内有无零点
合作交流 :
猜想:若函数在区间[a,b]上图象是连续的,如果有 成立,那么函数区间(a,b)上有零点。
f(a)·f(b)< 0
有
<
有
<
有
<
如果函数
的一条曲线,并且 ,
(a,b)内有零点,即存在
3. 零点存在性定理:
连续不断
那么
c也就是方程
f(a)·f(b)<0
(1)f(a)·f(b)<0则函数y=f(x)在区间(a,b)内有零点。
(2) 函数y=f(x)在区间(a,b)内有零点f(a)·f(b)<0。
(3) f(a)·f(b)<0 函数y=f(x)在区间(a,b)内只有一个零点。
注意:
1 函数是连续的。
定理辨析:
错
错
错
2 定理不可逆。
3 至少存在一个零点。
2.已知函数f(x)的图象是连续不断的,有如下对应值表:
??
那么函数在区间[1,6]上的零点至少有(? )个?
?A.5个?????? B.4个??? ??? C.3个?????? D.2个
C
巩固训练
1. f(x)=x3+x-1在下列哪个区间上有零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
B
x 1 2 3 4 5 6 7
f(x) 23 9 -7 11 -5 -12 -26
3.方程 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解法二:
三、求函数零点或零点个数的方法:
(1)定义法:解方程 f(x)=0,
得出函数的零点。
(3)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。
(2)定理法:函数零点存在性定理。
观察如上三个函数图像
思考:函数要满足什么条件在区间[a,b]上至多只有一个有零点?
函数在区间[a,b]上是单调连续的,则函数在区间[a,b]至多只有一个零点。
探究2:
0
0
0
a
b
y
x
y
x
y
x
一元二次方程的根及其相应
二次函数的图象与x轴交点的关系;
函数零点的概念;
函数零点与方程的根的关系;
函数零点存在性定理.
小结
布置作业:
P92 习题3.1 第2题
随堂检测
1.函数f(x)=x(x2-16)的零点为( ? )
A. (0,0),(4,0)?? ?? B.0,4????
C. (–4,0),(0,0),(4,0)??? D.–4,0,4
D
3.已知函数f(x)是定义域为R的奇函数,且f(x)在(0,+∞)上有一个零点,则f(x)的零点个数为(?? )
A.3????? B.2???? C.1???? D.不确定
A
4.若函数 仅有一个零点,求实数a的取值范围。
练习:
1.利用函数图象判断下列方程有没有根,有几个根:
(1)-x2+3x+5=0;
(2)2x(x-2)=-3;
(3) x2 =4x-4;
(4)5 x2 +2x=3 x2 +5.
2.利用函数的图象,指出下列函数零点所在的大致区间:
(1)f(x)= -x3-3x+5;
(2)f(x)=2x · ln(x-2)-3;
(3)f(x)=ex-1+4x-4;
(4)f(x)=3(x+2)(x-3)(x+4)+x.
有
没有
有
没有
有
没有
有
没有
1(1)解:令f(x)=-x2+3x+5,
作出函数f(x)的图象,如下:
它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根。
(1) -x2+3x+5=0
1(2)解:2x(x-2)=-3可化为
2x2-4x+3=0,令f(x)= 2x2-4x+3 , 作出函数f(x)的图象,如下:
它与x轴没有交点,所以方程2x(x-2)=-3无实数根。
(2) 2x(x-2)=-3
1(3)解:x2 =4x-4可化为x2-4x+4 =0,令f(x)= x2-4x+4,作出
函数f(x)的图象,如下:
它与x轴只有一个交点,所以方程x2 =4x-4有两个相等的实数根。
(3) x2 =4x-4
1(4)解:5x2 +2x=3x2 +5可化为
2x2 +2x-5=0,令f(x)= 2x2 +2x-5, 作出函数f(x)的图象,
如下:
它与x轴有两个交点,所以
方程5x2 +2x=3x2 +5有两个不
相等的实数根。
(4) 5 x2 +2x=3 x2 +5
2(1)解:作出函数的图象,如下:
因为f(1)=1>0,f(1.5)=-2.875<0,
所以f(x)= -x3-3x+5在区间(1, 1.5)
上有零点。又因为f(x)是(-∞,+∞)
上的减函数,所以在区间(1, 1.5)上有
且只有一个零点。
2(1) f(x)= -x3-3x+5
2(2)解:作出函数的图象,如下:
因为f(3)=-3<0,f(4)≈2.545>0,所以f(x)=
2x · ln(x-2)-3在区间(3,4)上有零点。又因为
f(x) =2x · ln(x-2)-3是(2,+∞)上的增函数,
所以在区间(3,4)上有且只有一个零点。
2(2) f(x)=2x · ln(x-2)-3
2(3)解:作出函数的图象,如下:
因为f(0)≈-3.63<0,f(1)
=1>0,所以f(x)= ex-1+4x-4
在区间(0,1)上有零点。又因
为f(x) = ex-1+4x-4是(-∞ ,
+∞)上的增函数,所以在
区间(0,1)上有且只有一个零
点。
2(3) f(x)=ex-1+4x-4
2(4)解:作出函数的图象,如下:
因为f(-4)=-4<0,f(- 3)=15>0,
f(-2)=-2<0,f(2)=-70<0, f(3)=3>0,
所以f(x)= 3(x+2)(x - 3)(x+4)+x 在区间
(-4,-3 )、 (-3,-2,)、 (2,3 )上各有
一个零点。
2(4) f(x)=3(x+2)(x-3)(x+4)+x
