1.1.3_四种命题间的相互关系(共30张PPT)
文档属性
| 名称 | 1.1.3_四种命题间的相互关系(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 354.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
1.1.3 四种命题间的相互关系
1. 四种命题的形式:
原命题:若p,则q.
则:
逆命题:若q,则p.
否命题:若¬p,则¬q
逆否命题:若¬q,则¬p.
原命题
(若p,则q)
逆命题
(若q,则p)
否命题
(若┐ p,则┐ q)
逆否命题
(若┐ q,则┐ p)
互逆
互逆
互否
互否
互为 逆否
互
为
逆
否
一:四种命题间的相互关系
原命题:若a>b,则a+c>b+c
逆命题:若a+c>b+c,则a>b
原命题:若四边形是正方形,则四边形两对角线垂直。
逆命题:若四边形两对角线垂直,则四边形是正方形。
原命题:若a>b,则ac2>bc2
逆命题:若ac2>bc2,则a>b
原命题:若四边形对角线相等,则四边形是平行四边形。
逆命题:若四边形是平行四边形,则四边形对角线相等。
真
真
真
假
假
真
假
假
判断下列命题的真假,并总结规律。
1.互逆命题的真假关系
(二)四种命题的真假关系
(1)
(2)
(3)
(4)
结 论 1
原命题的真假和逆命题的真假没有必然关系。
原命题:若a>b,则a+c>b+c
否命题:若a≤b,则a+c≤b+c
原命题:若四边形是正方形,则四边形两对角线垂直。
否命题:若四边形不是正方形,则四边形两对角线不垂直。
原命题:若a>b,则ac2>bc2
否命题:若a≤b,则ac2≤bc2
原命题:若四边形对角线相等,则四边形是平行四边形。
否命题:若四边形对角线不相等,则四边形不是平行四边形。
真
真
真
假
假
真
假
假
2.互否命题的真假关系
判断下列命题的真假,并总结规律。
结 论 2
原命题的真假和否命题的真假没有必然关系。
原命题:若a>b,则a+c>b+c
逆否命题:若a+c≤b+c,则a≤b
原命题:若四边形是正方形,则四边形两对角线垂直。
逆否命题:若四边形两对角线不垂直,则四边形不是正方形。
原命题:若a>b,则ac2>bc2
逆否命题:若ac2≤bc2,则a≤b
原命题:若四边形对角线相等,则四边形是平行四边形。
逆否命题:若四边形不是平行四边形,则四边形对角线不相等。
真
真
真
真
假
假
假
假
3.互为逆否命题的真假关系
判断下列命题的真假,并总结规律。
结 论 3
原命题和逆否命题总是同真同假。
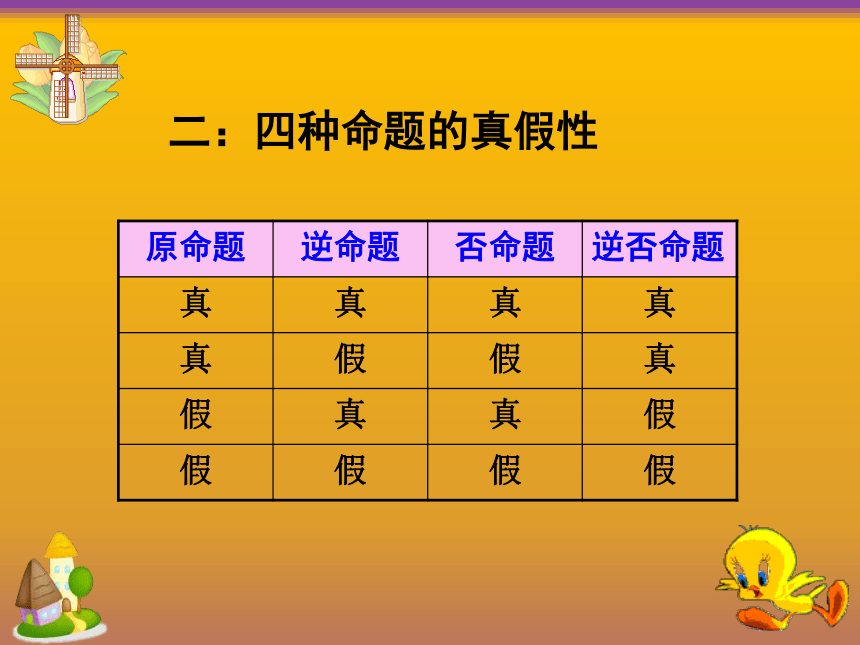
二:四种命题的真假性
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.
三:四种命题真假性间的关系
1.判断下列说法是否正确.
1)一个命题的逆命题为真,它的逆否命题不一定为真.
(对)
2)一个命题的否命题为真,它的逆命题一定为真.
(对)
2.四种命题真假的个数可能为( )个.
答:0、2、4.
如:原命题:若A∪B=A, 则A∩B=φ.
逆命题:若A∩B=φ,则A∪B=A.
否命题:若A∪B≠A,则A∩B≠φ.
逆否命题:若A∩B≠φ,则A∪B≠A.
(假)
(假)
(假)
(假)
3)一个命题的原命题为假,它的逆命题一定为假.
(错)
4)一个命题的逆否命题为假,它的否命题为假.
(错)
练一练
总结
反证法
要证明某一结论A是正确的,但不直接证明,而是先去证明A的反面(非A)是错误的,从而断定A是正确的.
即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论,完成命题的论证的一种数学证明方法.
反证法的一般步骤:
(1)假设命题的结论不成立 , 即假
设结论的反面成立;
(2)从这个假设出发 , 经过推理论证 ,
得出矛盾;
(3)由矛盾判定假设不正确 , 从而肯定
命题的结论正确.
反设
归谬
结论
例 证明:若p2+q2=2,则p+q≤2.
将“若p2+q2=2,则p+q≤2”看成原命题.由于原命题和它的逆否命题具有相同的真假性,要证原命题为真命题,可以证明它的逆否命题为真命题.
即证明 为真命题
假设原命题结论的反面成立
看能否推出原命题条件的反面成立
尝试成功
得证
例 证明:若p2+q2=2,则p+q≤2.
可能出现矛盾的四种情况:
与题设矛盾;
与反设矛盾;
与公理、定理矛盾;
在证明过程中,推出自相矛盾的结论.
由于原命题和它的逆否命题有相同的真假性,所以在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.
课堂小结
1.四种命题的相互关系:
互否
原命题
若p,则q
逆命题
若q,则p
逆否命题
若┐q,则┐p
否命题
若┐p,则┐q
互逆
互逆
互否
互
为
逆
否
互
为
逆
否
2.四种命题真假性的四种情况:
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
3.四种命题真假性的关系:
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.
练习题解答
1. 证明:若a-b=1,则
a2-b2+2a-4b-3
=(a+b)(a-b)+2(a-b)-2b-3
=a-b-1
=0
所以,原命题的逆否命题是真命题,从而原 命题也是真命题.
高考链接
1. (2008山东文)给出命题:若函数是幂函数,则函数的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
A.3 B.2 C.1 D.0
C
解析:由于原命题与逆否命题同真假性,逆命题与否命题同真假性,所以,原命题是真命题,则逆否命题也是真命题;否命题是假命题,则逆命题也是假命题.
2. (2001江西、山西、天津文、理)在空间中,
①若四点不共面,则这四点中任何三点都不共线.
②若两条直线没有共点,则这两条直线是异面直线.
以上两个命题中,逆命题为真命题的是 .(把符合要求的命题序号都填上)
②
解析:由于逆命题与否命题的真假性相同,那么②的否命题“若两条直线有公共点,则这两条直线不是异面直线”是真命题,所以它的逆命题也是真命题.
2.选择题
(1)设原命题:若a+b ≥2,则a,b 中至少有一个不小于1,则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
A
(2) 命题“若a>b则ac>bc”(这里a、b、c都是实数)与它的逆命题,否命题、逆否命题中,真命题的个数为( )
A.4 B.3
C.2 D.0
D
(1) 命题“已知a,b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0.”写出该命题的逆命题,否命题,逆否命题,并判断真假.
3.解答题:
解:逆命题“已知a,b为实数,若a2- 4b≥0,
则x2+ax+b≤0有非空解集.”
否命题“已知a,b为实数,若x2+ax+
b≤0没有非空解集,则a2-4b<0”
逆否命题“已知a,b为实数,若a2-4b <0,
则x2+ax+b≤0没有非空解集”
原命题,逆命题,否命题,逆否命题均为真命题.
1.1.3 四种命题间的相互关系
1. 四种命题的形式:
原命题:若p,则q.
则:
逆命题:若q,则p.
否命题:若¬p,则¬q
逆否命题:若¬q,则¬p.
原命题
(若p,则q)
逆命题
(若q,则p)
否命题
(若┐ p,则┐ q)
逆否命题
(若┐ q,则┐ p)
互逆
互逆
互否
互否
互为 逆否
互
为
逆
否
一:四种命题间的相互关系
原命题:若a>b,则a+c>b+c
逆命题:若a+c>b+c,则a>b
原命题:若四边形是正方形,则四边形两对角线垂直。
逆命题:若四边形两对角线垂直,则四边形是正方形。
原命题:若a>b,则ac2>bc2
逆命题:若ac2>bc2,则a>b
原命题:若四边形对角线相等,则四边形是平行四边形。
逆命题:若四边形是平行四边形,则四边形对角线相等。
真
真
真
假
假
真
假
假
判断下列命题的真假,并总结规律。
1.互逆命题的真假关系
(二)四种命题的真假关系
(1)
(2)
(3)
(4)
结 论 1
原命题的真假和逆命题的真假没有必然关系。
原命题:若a>b,则a+c>b+c
否命题:若a≤b,则a+c≤b+c
原命题:若四边形是正方形,则四边形两对角线垂直。
否命题:若四边形不是正方形,则四边形两对角线不垂直。
原命题:若a>b,则ac2>bc2
否命题:若a≤b,则ac2≤bc2
原命题:若四边形对角线相等,则四边形是平行四边形。
否命题:若四边形对角线不相等,则四边形不是平行四边形。
真
真
真
假
假
真
假
假
2.互否命题的真假关系
判断下列命题的真假,并总结规律。
结 论 2
原命题的真假和否命题的真假没有必然关系。
原命题:若a>b,则a+c>b+c
逆否命题:若a+c≤b+c,则a≤b
原命题:若四边形是正方形,则四边形两对角线垂直。
逆否命题:若四边形两对角线不垂直,则四边形不是正方形。
原命题:若a>b,则ac2>bc2
逆否命题:若ac2≤bc2,则a≤b
原命题:若四边形对角线相等,则四边形是平行四边形。
逆否命题:若四边形不是平行四边形,则四边形对角线不相等。
真
真
真
真
假
假
假
假
3.互为逆否命题的真假关系
判断下列命题的真假,并总结规律。
结 论 3
原命题和逆否命题总是同真同假。
二:四种命题的真假性
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.
三:四种命题真假性间的关系
1.判断下列说法是否正确.
1)一个命题的逆命题为真,它的逆否命题不一定为真.
(对)
2)一个命题的否命题为真,它的逆命题一定为真.
(对)
2.四种命题真假的个数可能为( )个.
答:0、2、4.
如:原命题:若A∪B=A, 则A∩B=φ.
逆命题:若A∩B=φ,则A∪B=A.
否命题:若A∪B≠A,则A∩B≠φ.
逆否命题:若A∩B≠φ,则A∪B≠A.
(假)
(假)
(假)
(假)
3)一个命题的原命题为假,它的逆命题一定为假.
(错)
4)一个命题的逆否命题为假,它的否命题为假.
(错)
练一练
总结
反证法
要证明某一结论A是正确的,但不直接证明,而是先去证明A的反面(非A)是错误的,从而断定A是正确的.
即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论,完成命题的论证的一种数学证明方法.
反证法的一般步骤:
(1)假设命题的结论不成立 , 即假
设结论的反面成立;
(2)从这个假设出发 , 经过推理论证 ,
得出矛盾;
(3)由矛盾判定假设不正确 , 从而肯定
命题的结论正确.
反设
归谬
结论
例 证明:若p2+q2=2,则p+q≤2.
将“若p2+q2=2,则p+q≤2”看成原命题.由于原命题和它的逆否命题具有相同的真假性,要证原命题为真命题,可以证明它的逆否命题为真命题.
即证明 为真命题
假设原命题结论的反面成立
看能否推出原命题条件的反面成立
尝试成功
得证
例 证明:若p2+q2=2,则p+q≤2.
可能出现矛盾的四种情况:
与题设矛盾;
与反设矛盾;
与公理、定理矛盾;
在证明过程中,推出自相矛盾的结论.
由于原命题和它的逆否命题有相同的真假性,所以在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.
课堂小结
1.四种命题的相互关系:
互否
原命题
若p,则q
逆命题
若q,则p
逆否命题
若┐q,则┐p
否命题
若┐p,则┐q
互逆
互逆
互否
互
为
逆
否
互
为
逆
否
2.四种命题真假性的四种情况:
原命题 逆命题 否命题 逆否命题
真 真 真 真
真 假 假 真
假 真 真 假
假 假 假 假
3.四种命题真假性的关系:
(1)两个命题互为逆否命题,它们有相同的真假性.
(2)两个命题互为逆命题或互为否命题,它们的真假性没有关系.
练习题解答
1. 证明:若a-b=1,则
a2-b2+2a-4b-3
=(a+b)(a-b)+2(a-b)-2b-3
=a-b-1
=0
所以,原命题的逆否命题是真命题,从而原 命题也是真命题.
高考链接
1. (2008山东文)给出命题:若函数是幂函数,则函数的图象不过第四象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
A.3 B.2 C.1 D.0
C
解析:由于原命题与逆否命题同真假性,逆命题与否命题同真假性,所以,原命题是真命题,则逆否命题也是真命题;否命题是假命题,则逆命题也是假命题.
2. (2001江西、山西、天津文、理)在空间中,
①若四点不共面,则这四点中任何三点都不共线.
②若两条直线没有共点,则这两条直线是异面直线.
以上两个命题中,逆命题为真命题的是 .(把符合要求的命题序号都填上)
②
解析:由于逆命题与否命题的真假性相同,那么②的否命题“若两条直线有公共点,则这两条直线不是异面直线”是真命题,所以它的逆命题也是真命题.
2.选择题
(1)设原命题:若a+b ≥2,则a,b 中至少有一个不小于1,则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
A
(2) 命题“若a>b则ac>bc”(这里a、b、c都是实数)与它的逆命题,否命题、逆否命题中,真命题的个数为( )
A.4 B.3
C.2 D.0
D
(1) 命题“已知a,b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0.”写出该命题的逆命题,否命题,逆否命题,并判断真假.
3.解答题:
解:逆命题“已知a,b为实数,若a2- 4b≥0,
则x2+ax+b≤0有非空解集.”
否命题“已知a,b为实数,若x2+ax+
b≤0没有非空解集,则a2-4b<0”
逆否命题“已知a,b为实数,若a2-4b <0,
则x2+ax+b≤0没有非空解集”
原命题,逆命题,否命题,逆否命题均为真命题.
