18.4 相似多边形 课件(23张PPT)
文档属性
| 名称 | 18.4 相似多边形 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览







文档简介
课件23张PPT。相似多边形相似多边形经历相似多边形概念的形成过程,了解相似多边形的含义
知道相似多边形的对应角相等,对应边成比例
在探索相似多边形的过程中,进一步发展自身类比,反思、交流等方面的能力,提高数学思维水平,体会公例的作用.知识点框架问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗?复习旧课ABCDEFA1B1C1D1E1F1观察以下两个多边形,并回答如下问题:(1)在下图中两个多边形中,是否有相等的内角?设法验证.
(2)在下图中两个多边形中,相等内角的两边是否成比例?新课进行下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?(1)正三角形ABC与正三角形DEF;解:∵正三角形每个角都等于60 ° ,
∴∠A =∠D = 60°,∠B =∠E = 60 ° ,
∠C =∠F = 60 ° ,∴这两个正三角形的对应角相等
又∵正三角形三边相等
∴AB/DE = BC/EF = CA/FD
∴这两个正三角形的对应边的比相等(即对应边成比例)ABCDEF新知讲解(2)正方形ABCD与正方EFGH它们的对应角有怎样的关系?对应边呢?解:∵正方形每个角都等于90°,
∴∠A =∠E = 90 ° , ∠B =∠F = 90 ° ,
∠C =∠G = 90 ° , ∠D =∠H = 90 °
∴这两个正方形的对应角相等
又∵正方形的四边相等
∴AB/EF = BC/FG = CD/GH = DA/HE
∴这两个正方形的对应边的比相等(即对应边成比例)ABCDEFGH重要问题学法指导 问题 相似多边形
对应角相等,对应边成比例的两个多边形叫做相似多边形,相似多边形的对应边的比叫做相似比.证明两个多边形相似的条件:1 对应角相等
2 对应边成比例若四边形ABCD与四边形EFGH相似,可记作:
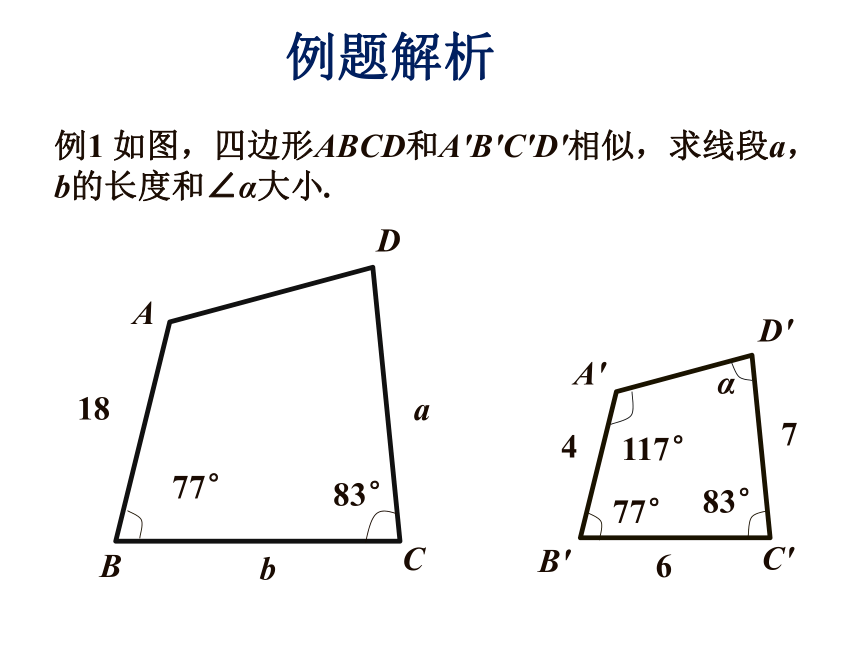
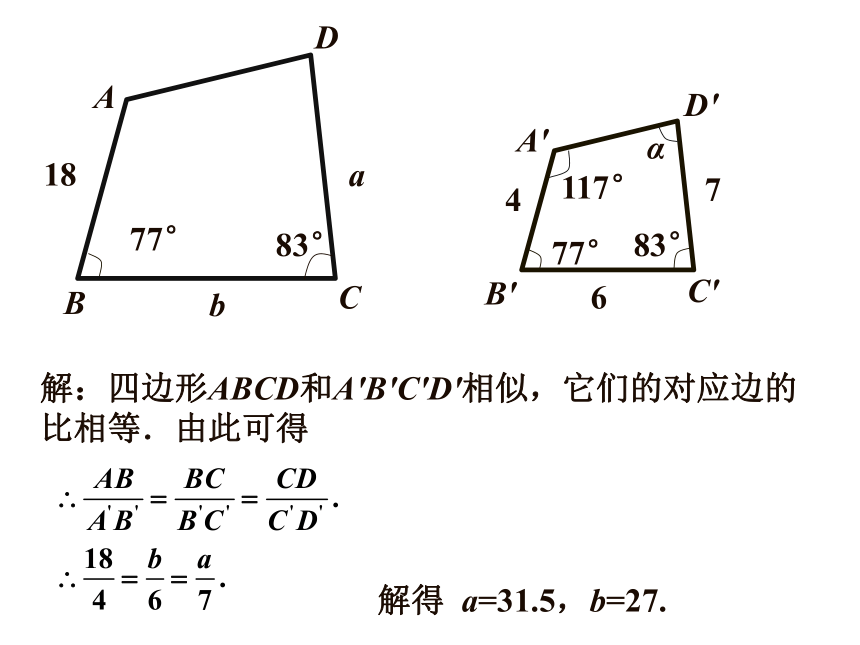
四边形ABCD∽四边形EFGH{例1 如图,四边形ABCD和A'B'C'D'相似,求线段a,b的长度和∠α大小.例题解析解:四边形ABCD和A'B'C'D'相似,它们的对应边的比相等.由此可得解得 a=31.5,b=27.在相似多边形中,最简单的是相似三角形.如图,在△ABC和△ A'B'C'中,如果有∠A=∠ A' ,∠B=∠ B' ,∠C=∠ C' ,那么△ABC和△相似,记作“△ABC∽ △A'B'C'”.例2、已知:如图,△ADE与△ACB相似,指出他们的对应顶点、对应边和对应角.解:对应顶点:A和A,D和C,E和B.
对应边:AD和AC,AE和AB,DE和CB.
对应角:∠A和∠A,∠ADE和∠C,∠AED和∠B.例3、已知:如图,△ADE与△ACB相似,AE=50cm, EC=30cm, BC=70cm,∠ A=45°,
∠ C=45°.求:
(1) ∠ AED和∠ ADE的度数.
(2)DE的长.解:(1)因为 △ABC∽ △A'B'C' ,
所以∠AED= ∠C=40°.
在△ADE中,
因为∠AED+ ∠ADE+ ∠A=180°,
即40°+ ∠ ADE+45°=180°.
所以∠ ADE=95°.(2)因为 △ABC∽ △A'B'C' ,即cm解题方法 技巧 策略题型1 判断两个多边形相似1 判断下列每组图形是否相似,为什么?5正方形55正方形566610菱形长方形(1)(2)解:(1)∵正方形,菱形的四条边都相等
∴它们的对应边一定成比例
(如上图对边应的比是 5/6)
∵正方形的四个 内角均为直角,而菱形的内角有钝角有锐角
∴它们的对应角不相等
∴这一组图形不相似(2) ∵正方形和矩形的四个内角都是直角
∴它们的对应角相等
∵对应边 5/6≠5/10
∴对应边不成比例
∴这一组图形也不相似2 一块长3m,宽1.5m的矩形黑板如图,镶其外围的木质边宽7.5cm.边框内外边缘所组成的矩形相似吗?为什么?3m1.5mDG(300+2×7.5)cm(150+2×7.5)cmEFBACH解: ∵矩形的每个内角都等于90° ∴∠A=∠E=90 ° , ∠B=∠F=90o, ∠H=90 ° ,∠D=∠G=90 ° ∴它们的对应角相等∵AB/EF=300/(300+2×7.5)=20/21
BC/FH=150/(150+2×7.5)=10/11
∴AB/EF≠BC/FH
∴ 矩形ABCD和矩形EFGH不相似题型2 求相似多边形的对应角或对应边已知,如图,五边形ABCDE∽五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90 °
求:(1)相似比等于多少?
(2)FG,IJ,BC,AE, ∠F, ∠CAFGHIJ解:(1)相似比=CD/HI=3/5
(2) ∵五边形ABCDE∽五边形FGHIJ
∴ ∠F =∠A=120°, ∠C= ∠H=90 ° ,
∴AB/FG=BC/GH=CD/HI=DE/IJ=EA/JF
即2/FG=BC/6=3/5=2.2/IJ=AE/4
解得FG=10/3cm,BC=18/5cm,IJ=11/3cm,AE=12/5cm1.相似多边形定义:小结: 对应角相等,且对应边成比例的两个多边形叫做相似多边形.2.相似多边形的对应边的比k叫作相似比.3.相似多边形的性质: 相似多边形的对应角相等,对应边成比例.再 见
知道相似多边形的对应角相等,对应边成比例
在探索相似多边形的过程中,进一步发展自身类比,反思、交流等方面的能力,提高数学思维水平,体会公例的作用.知识点框架问题:用同一张底片洗出不同尺寸的照片,两张图片相似吗?复习旧课ABCDEFA1B1C1D1E1F1观察以下两个多边形,并回答如下问题:(1)在下图中两个多边形中,是否有相等的内角?设法验证.
(2)在下图中两个多边形中,相等内角的两边是否成比例?新课进行下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?(1)正三角形ABC与正三角形DEF;解:∵正三角形每个角都等于60 ° ,
∴∠A =∠D = 60°,∠B =∠E = 60 ° ,
∠C =∠F = 60 ° ,∴这两个正三角形的对应角相等
又∵正三角形三边相等
∴AB/DE = BC/EF = CA/FD
∴这两个正三角形的对应边的比相等(即对应边成比例)ABCDEF新知讲解(2)正方形ABCD与正方EFGH它们的对应角有怎样的关系?对应边呢?解:∵正方形每个角都等于90°,
∴∠A =∠E = 90 ° , ∠B =∠F = 90 ° ,
∠C =∠G = 90 ° , ∠D =∠H = 90 °
∴这两个正方形的对应角相等
又∵正方形的四边相等
∴AB/EF = BC/FG = CD/GH = DA/HE
∴这两个正方形的对应边的比相等(即对应边成比例)ABCDEFGH重要问题学法指导 问题 相似多边形
对应角相等,对应边成比例的两个多边形叫做相似多边形,相似多边形的对应边的比叫做相似比.证明两个多边形相似的条件:1 对应角相等
2 对应边成比例若四边形ABCD与四边形EFGH相似,可记作:
四边形ABCD∽四边形EFGH{例1 如图,四边形ABCD和A'B'C'D'相似,求线段a,b的长度和∠α大小.例题解析解:四边形ABCD和A'B'C'D'相似,它们的对应边的比相等.由此可得解得 a=31.5,b=27.在相似多边形中,最简单的是相似三角形.如图,在△ABC和△ A'B'C'中,如果有∠A=∠ A' ,∠B=∠ B' ,∠C=∠ C' ,那么△ABC和△相似,记作“△ABC∽ △A'B'C'”.例2、已知:如图,△ADE与△ACB相似,指出他们的对应顶点、对应边和对应角.解:对应顶点:A和A,D和C,E和B.
对应边:AD和AC,AE和AB,DE和CB.
对应角:∠A和∠A,∠ADE和∠C,∠AED和∠B.例3、已知:如图,△ADE与△ACB相似,AE=50cm, EC=30cm, BC=70cm,∠ A=45°,
∠ C=45°.求:
(1) ∠ AED和∠ ADE的度数.
(2)DE的长.解:(1)因为 △ABC∽ △A'B'C' ,
所以∠AED= ∠C=40°.
在△ADE中,
因为∠AED+ ∠ADE+ ∠A=180°,
即40°+ ∠ ADE+45°=180°.
所以∠ ADE=95°.(2)因为 △ABC∽ △A'B'C' ,即cm解题方法 技巧 策略题型1 判断两个多边形相似1 判断下列每组图形是否相似,为什么?5正方形55正方形566610菱形长方形(1)(2)解:(1)∵正方形,菱形的四条边都相等
∴它们的对应边一定成比例
(如上图对边应的比是 5/6)
∵正方形的四个 内角均为直角,而菱形的内角有钝角有锐角
∴它们的对应角不相等
∴这一组图形不相似(2) ∵正方形和矩形的四个内角都是直角
∴它们的对应角相等
∵对应边 5/6≠5/10
∴对应边不成比例
∴这一组图形也不相似2 一块长3m,宽1.5m的矩形黑板如图,镶其外围的木质边宽7.5cm.边框内外边缘所组成的矩形相似吗?为什么?3m1.5mDG(300+2×7.5)cm(150+2×7.5)cmEFBACH解: ∵矩形的每个内角都等于90° ∴∠A=∠E=90 ° , ∠B=∠F=90o, ∠H=90 ° ,∠D=∠G=90 ° ∴它们的对应角相等∵AB/EF=300/(300+2×7.5)=20/21
BC/FH=150/(150+2×7.5)=10/11
∴AB/EF≠BC/FH
∴ 矩形ABCD和矩形EFGH不相似题型2 求相似多边形的对应角或对应边已知,如图,五边形ABCDE∽五边形FGHIJ,且AB=2cm,CD=3cm,DE=2.2cm,GH=6cm,HI =5cm,FJ=4cm, ∠A=120°,∠H=90 °
求:(1)相似比等于多少?
(2)FG,IJ,BC,AE, ∠F, ∠CAFGHIJ解:(1)相似比=CD/HI=3/5
(2) ∵五边形ABCDE∽五边形FGHIJ
∴ ∠F =∠A=120°, ∠C= ∠H=90 ° ,
∴AB/FG=BC/GH=CD/HI=DE/IJ=EA/JF
即2/FG=BC/6=3/5=2.2/IJ=AE/4
解得FG=10/3cm,BC=18/5cm,IJ=11/3cm,AE=12/5cm1.相似多边形定义:小结: 对应角相等,且对应边成比例的两个多边形叫做相似多边形.2.相似多边形的对应边的比k叫作相似比.3.相似多边形的性质: 相似多边形的对应角相等,对应边成比例.再 见
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
