北京课改版九年级上册18.5 相似三角形的判定 课件(25张PPT)
文档属性
| 名称 | 北京课改版九年级上册18.5 相似三角形的判定 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 11:31:59 | ||
图片预览







文档简介
课件25张PPT。相似三角形的判定一、复习引入.1、相似三角形的定义是什么? 如果那么△ABC∽△A'B'C'2、相似三角形与全等三角形有什么内在的联系呢? 全等三角形是相似比为1的特殊的相似三角形. ∠A=∠A',∠B=∠B',∠C=∠ C' 如图在△ABC中,点D,E分别在AB,AC上,且DE ∥ BC,则△ADE与△ABC相似吗?
(1)议一议:这两个三角形的三个内角是否对应相等?
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.合作学习:ABCDE归纳:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A探究题:已知在△ABC 和△ A'B'C' 中,
∠A=∠A',∠B=∠B',求证:△ABC∽△A'B'C'分析:要证两个三角形相似,
目前只有两个途径.一个是三角形相似的定义,(显然条件不具备);
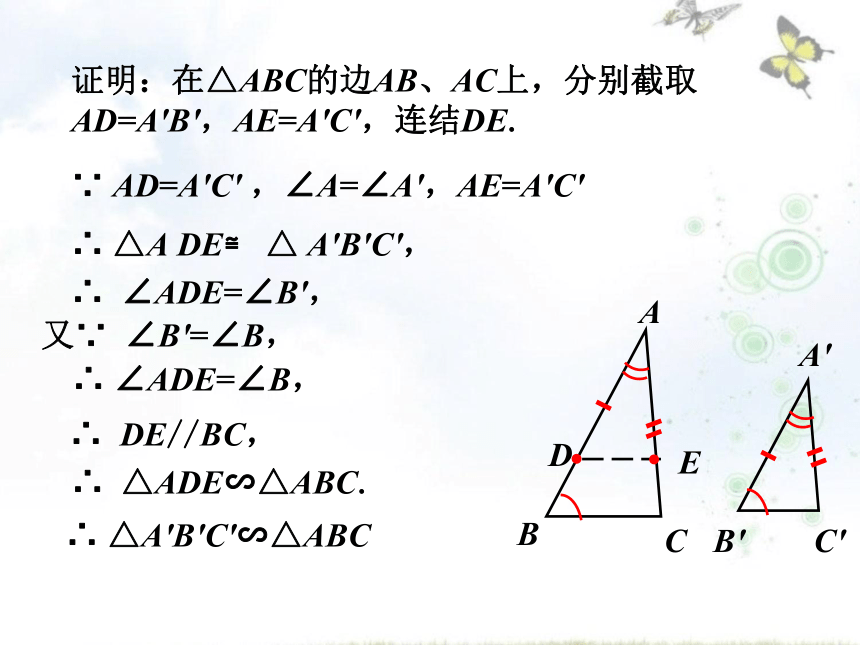
二个利用平行线来判定三角形相似的定理.为了使用它,就必须创造具备定理的基本图形的条件.怎样创造呢?(把小的三角形移动到大的三角形上).怎样实现移动呢?证明:在△ABC的边AB、AC上,分别截取AD=A'B',AE=A'C',连结DE.BC' ∵ AD=A'C' ,∠A=∠A',AE=A'C'∴ △A DE≌ △ A'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ △ADE∽△ABC.∴ △A'B'C'∽△ABC由探究题可知:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:两角对应相等,两三角形相似.例1:如图,在 Rt△ABC 中,CD 是斜边 AB 上的高,请找出图中相似三角形,并说明理由.解:△ABC∽△CDB∽ △ACD.理由如下:
在Rt△ABC中
∵∠CDB=∠ACB=90°,∠B=∠B
∴△ABC∽△CDB
同理△ABC∽△ACD
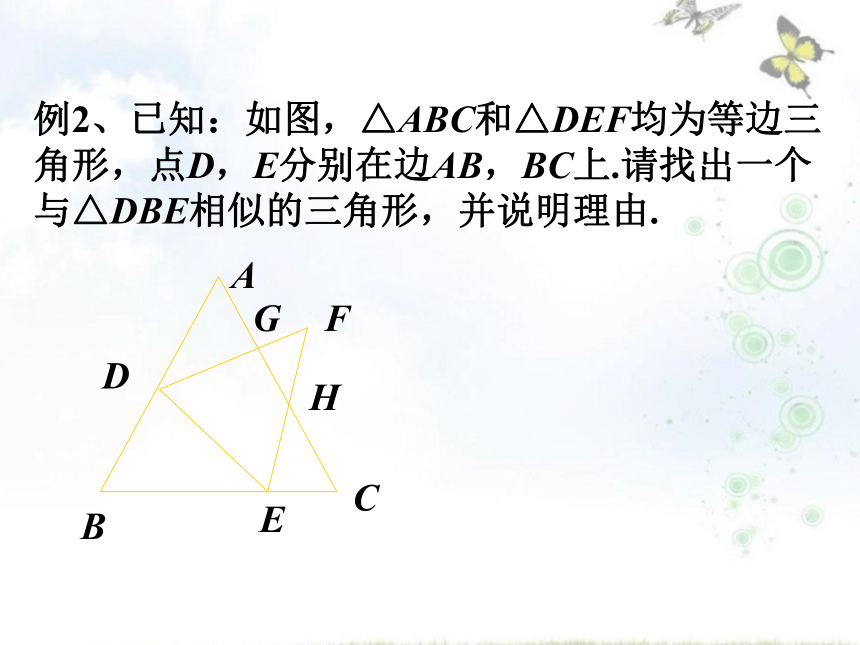
∴△ABC∽△CDB∽ △ACD例2、已知:如图,△ABC和△DEF均为等边三角形,点D,E分别在边AB,BC上.请找出一个与△DBE相似的三角形,并说明理由.解:△ECH与△DBE相似.理由如下:
在△DBE和△ECB中,∠B=∠C=60°.
∵∠BDE+∠BED=120°,∠BED+∠CEH=120°,
∴ ∠BDE=∠CEH.
∴ △DBE ∽△ECH.练习:已知:△ABC和△DEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°.
求证:△ABC∽△DEF B证明:∵ 在△ABC中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A -∠B =180°-40° -80° =60°
∵ 在ΔDEF中,∠E=80°,∠F=60°
∴ ∠B=∠E,∠C=∠F
∴ △ABC∽△DEF(两角对应相等,两三角形相似).课堂练习(1)、已知△ABC与△A'B'C'中,∠B=∠B ' =75°,∠C=50°,∠A ' =55°,这两个三角形相似吗?为什么?(2)已知等腰三角形△ABC和△A'B'C'中,∠A、∠A'分别是顶角,求证:①如果∠A=∠A',那么△ABC∽△A'B'C'.
②如果∠B=∠B',那么△ABC∽ △A'B'C'.C'练习题:求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:在RtΔABC中,CD是斜边AB上的高.证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,此结论可以称为“母子相似定理”,今后可以直接使用.∴ △ACD∽ △ABC(两角对应相等,两 三角形相似).同理 △CBD ∽ △ABC .∴ △ABC∽△ACD∽△CBD .求证:△ABC∽△ACD∽△CBD .如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
可简单说成:三边对应成比例,两三角形相似.几何格式:那么△ABC∽△A'B'C'练习:如图,Rt△ABC 中,∠C=90°,AB=10,AC=8.E 是 AC 上一点,AE=5,ED⊥AB,垂足为 D.求 AD 的长.解:∵ ED⊥AB,∴∠EDA=90°.又∠C=90°, ∠A= ∠A,∴△AED∽ △ABC如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.可以简单说成“两边对应成比例且夹角相等,两三角形相似”已知:如图,△A'B'C'和△ABC中,
∠A'=∠A,A'B':AB=A'C':AC
求证: △ABC∽△A'B'C'.几何格式:那么△ABC∽△A'B'C'∠A=∠A' 例3:根据下列条件,判断△ABC 和△A′B′C′是否相似,并说明理由:
(1)AB=4 cm,BC=6 cm,AC=8 cm,
A′B′=12 cm,B′C′=18 cm,A′C′=24 cm.解: 例3:根据下列条件,判断△ABC 和△A′B′C′是否相似,并说明理由:
(2)∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm,A′C′=6 cm.解:例4、已知△ABC,P是边AB上的一点,连接CP.
(1)当∠ACP满足什么条件时,△ACP∽△ABC?
(2)当AC:AP满足什么条件时,△ACP∽△ABC?解:(1)∵∠A=∠A,
∴当∠ACP=∠B时, △ACP∽△ABC.
(2)∵∠A=∠A,
∴当AC:AP=AB:AC时, △ACP∽△ABC.1.已知:在△ABC中,AB=AC;在△A′B′C′中,A′B′=A′C′.(1)如果∠A=∠A′,求证:△ABC∽△A′B′C′;
(2)如果∠B=∠B′,求证: △ABC∽ △ A′B′C′.课外练习证明:(1)∵ AB=AC,∴∠B=∠C= (180°-∠A).(等边对等角)
同理, ∠B′=∠C′= (180°-∠A).
又∵ ∠A=∠A′,∴∠B=∠B′, ∠C=∠C′.
∴ △ABC∽△A′B′C′.(2) ∵ AB=AC,∴∠B=∠C. (等边对等角)
同理, ∠B′=∠C′ .
又∵∠B=∠B′,所以∠C=∠C′.
∴ △ABC∽△A′B′C′.2.如果△ABC∽ △A1B1C1, △A1B1C1 ∽△A2B2C2,
那么△ABC与△A2B2C2有什么关系,为什么?它们相似.∵ △ABC∽ △A1B1C1,
∴这两个三角形的三个对应角相等.
又∵ △A1B1C1 ∽△A2B2C2,
∴ △A1B1C1 与△A2B2C2对应的三个角相等,则△ABC与 △A2B2C2对应角相等,故△ABC∽△A2B2C2.3.如图,在四边形ABCD中,DC∥AB,对角线AC交BD于点°.找出图中相似三角形,并写出它们对应边成比例的式子.△AB°∽△CD°体验收获 说一说你的收获 …… 1.三角形相似的定义;
2.平行线分线段成比例的基本事实、推论及在三角形中的运用;
3.三角形相似的判定方法.
(1)议一议:这两个三角形的三个内角是否对应相等?
(2)量一量这两个三角形的边长,它们是否对应成比例?平行移动DE的位置再试一试.合作学习:ABCDE归纳:
平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A探究题:已知在△ABC 和△ A'B'C' 中,
∠A=∠A',∠B=∠B',求证:△ABC∽△A'B'C'分析:要证两个三角形相似,
目前只有两个途径.一个是三角形相似的定义,(显然条件不具备);
二个利用平行线来判定三角形相似的定理.为了使用它,就必须创造具备定理的基本图形的条件.怎样创造呢?(把小的三角形移动到大的三角形上).怎样实现移动呢?证明:在△ABC的边AB、AC上,分别截取AD=A'B',AE=A'C',连结DE.BC' ∵ AD=A'C' ,∠A=∠A',AE=A'C'∴ △A DE≌ △ A'B'C',∴ ∠ADE=∠B',又∵ ∠B'=∠B,∴ ∠ADE=∠B,∴ DE//BC,∴ △ADE∽△ABC.∴ △A'B'C'∽△ABC由探究题可知:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
可以简单说成:两角对应相等,两三角形相似.例1:如图,在 Rt△ABC 中,CD 是斜边 AB 上的高,请找出图中相似三角形,并说明理由.解:△ABC∽△CDB∽ △ACD.理由如下:
在Rt△ABC中
∵∠CDB=∠ACB=90°,∠B=∠B
∴△ABC∽△CDB
同理△ABC∽△ACD
∴△ABC∽△CDB∽ △ACD例2、已知:如图,△ABC和△DEF均为等边三角形,点D,E分别在边AB,BC上.请找出一个与△DBE相似的三角形,并说明理由.解:△ECH与△DBE相似.理由如下:
在△DBE和△ECB中,∠B=∠C=60°.
∵∠BDE+∠BED=120°,∠BED+∠CEH=120°,
∴ ∠BDE=∠CEH.
∴ △DBE ∽△ECH.练习:已知:△ABC和△DEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°.
求证:△ABC∽△DEF B证明:∵ 在△ABC中,∠A=40°,∠B=80°,
∴ ∠C=180°-∠A -∠B =180°-40° -80° =60°
∵ 在ΔDEF中,∠E=80°,∠F=60°
∴ ∠B=∠E,∠C=∠F
∴ △ABC∽△DEF(两角对应相等,两三角形相似).课堂练习(1)、已知△ABC与△A'B'C'中,∠B=∠B ' =75°,∠C=50°,∠A ' =55°,这两个三角形相似吗?为什么?(2)已知等腰三角形△ABC和△A'B'C'中,∠A、∠A'分别是顶角,求证:①如果∠A=∠A',那么△ABC∽△A'B'C'.
②如果∠B=∠B',那么△ABC∽ △A'B'C'.C'练习题:求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.已知:在RtΔABC中,CD是斜边AB上的高.证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,此结论可以称为“母子相似定理”,今后可以直接使用.∴ △ACD∽ △ABC(两角对应相等,两 三角形相似).同理 △CBD ∽ △ABC .∴ △ABC∽△ACD∽△CBD .求证:△ABC∽△ACD∽△CBD .如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.
可简单说成:三边对应成比例,两三角形相似.几何格式:那么△ABC∽△A'B'C'练习:如图,Rt△ABC 中,∠C=90°,AB=10,AC=8.E 是 AC 上一点,AE=5,ED⊥AB,垂足为 D.求 AD 的长.解:∵ ED⊥AB,∴∠EDA=90°.又∠C=90°, ∠A= ∠A,∴△AED∽ △ABC如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.可以简单说成“两边对应成比例且夹角相等,两三角形相似”已知:如图,△A'B'C'和△ABC中,
∠A'=∠A,A'B':AB=A'C':AC
求证: △ABC∽△A'B'C'.几何格式:那么△ABC∽△A'B'C'∠A=∠A' 例3:根据下列条件,判断△ABC 和△A′B′C′是否相似,并说明理由:
(1)AB=4 cm,BC=6 cm,AC=8 cm,
A′B′=12 cm,B′C′=18 cm,A′C′=24 cm.解: 例3:根据下列条件,判断△ABC 和△A′B′C′是否相似,并说明理由:
(2)∠A=120°,AB=7 cm,AC=14 cm,
∠A′=120°,A′B′=3 cm,A′C′=6 cm.解:例4、已知△ABC,P是边AB上的一点,连接CP.
(1)当∠ACP满足什么条件时,△ACP∽△ABC?
(2)当AC:AP满足什么条件时,△ACP∽△ABC?解:(1)∵∠A=∠A,
∴当∠ACP=∠B时, △ACP∽△ABC.
(2)∵∠A=∠A,
∴当AC:AP=AB:AC时, △ACP∽△ABC.1.已知:在△ABC中,AB=AC;在△A′B′C′中,A′B′=A′C′.(1)如果∠A=∠A′,求证:△ABC∽△A′B′C′;
(2)如果∠B=∠B′,求证: △ABC∽ △ A′B′C′.课外练习证明:(1)∵ AB=AC,∴∠B=∠C= (180°-∠A).(等边对等角)
同理, ∠B′=∠C′= (180°-∠A).
又∵ ∠A=∠A′,∴∠B=∠B′, ∠C=∠C′.
∴ △ABC∽△A′B′C′.(2) ∵ AB=AC,∴∠B=∠C. (等边对等角)
同理, ∠B′=∠C′ .
又∵∠B=∠B′,所以∠C=∠C′.
∴ △ABC∽△A′B′C′.2.如果△ABC∽ △A1B1C1, △A1B1C1 ∽△A2B2C2,
那么△ABC与△A2B2C2有什么关系,为什么?它们相似.∵ △ABC∽ △A1B1C1,
∴这两个三角形的三个对应角相等.
又∵ △A1B1C1 ∽△A2B2C2,
∴ △A1B1C1 与△A2B2C2对应的三个角相等,则△ABC与 △A2B2C2对应角相等,故△ABC∽△A2B2C2.3.如图,在四边形ABCD中,DC∥AB,对角线AC交BD于点°.找出图中相似三角形,并写出它们对应边成比例的式子.△AB°∽△CD°体验收获 说一说你的收获 …… 1.三角形相似的定义;
2.平行线分线段成比例的基本事实、推论及在三角形中的运用;
3.三角形相似的判定方法.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
