北京课改版九年级上册18.6 相似三角形的性质 课件(20张PPT)
文档属性
| 名称 | 北京课改版九年级上册18.6 相似三角形的性质 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 234.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 11:34:57 | ||
图片预览


文档简介
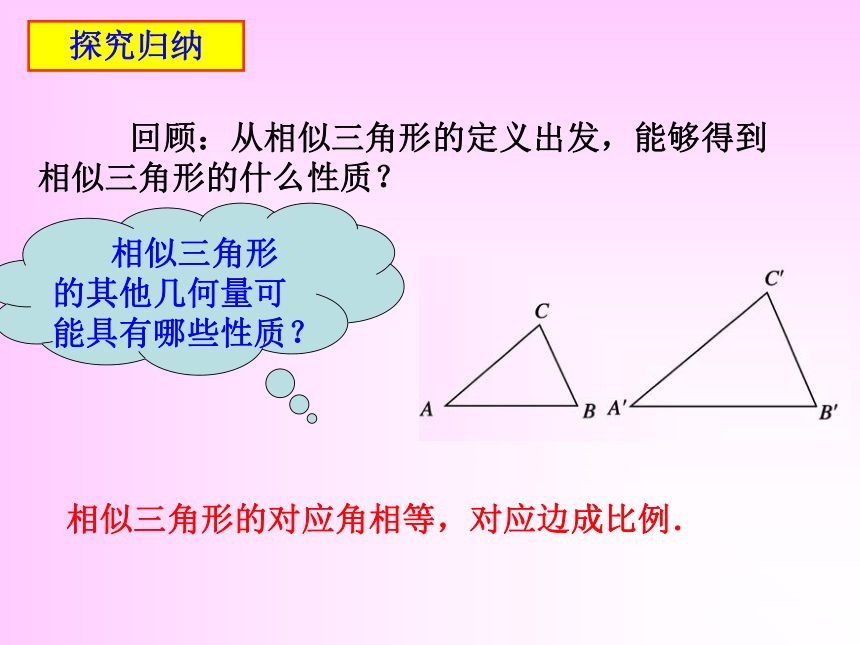
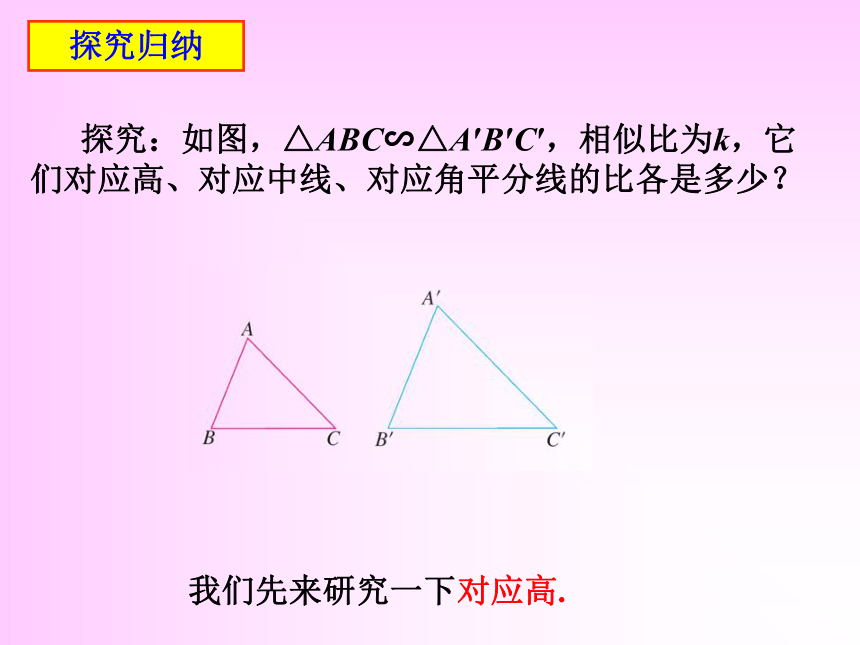
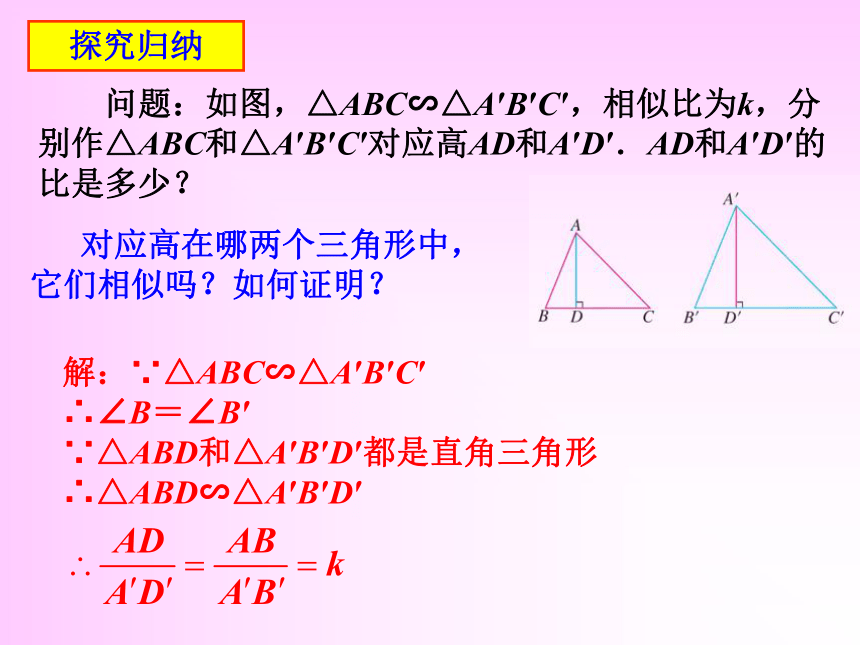
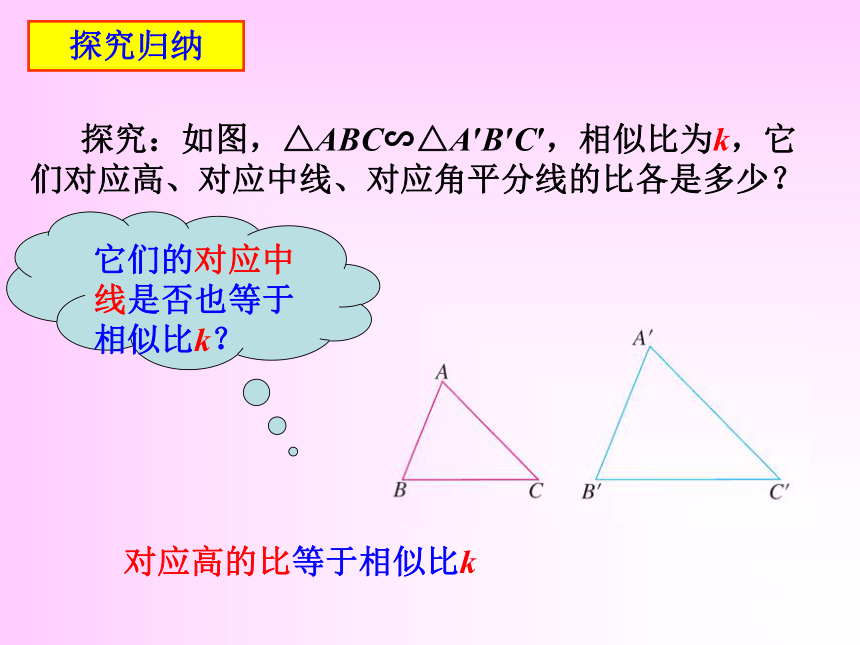
课件20张PPT。相似三角形的性质情境引入 三角形中有各种各样的几何量.三条边的长度三个内角的度数周长、面积等等高、中线、角平分线的长度如: 如果两个三角形相似,那么它们的这些几何量之间有什么关系呢? 探究归纳 回顾:从相似三角形的定义出发,能够得到相似三角形的什么性质?相似三角形的对应角相等,对应边成比例. 相似三角形的其他几何量可能具有哪些性质? 探究归纳 探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?我们先来研究一下对应高.探究归纳 问题:如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′都是直角三角形
∴△ABD∽△A′B′D′ 对应高在哪两个三角形中,
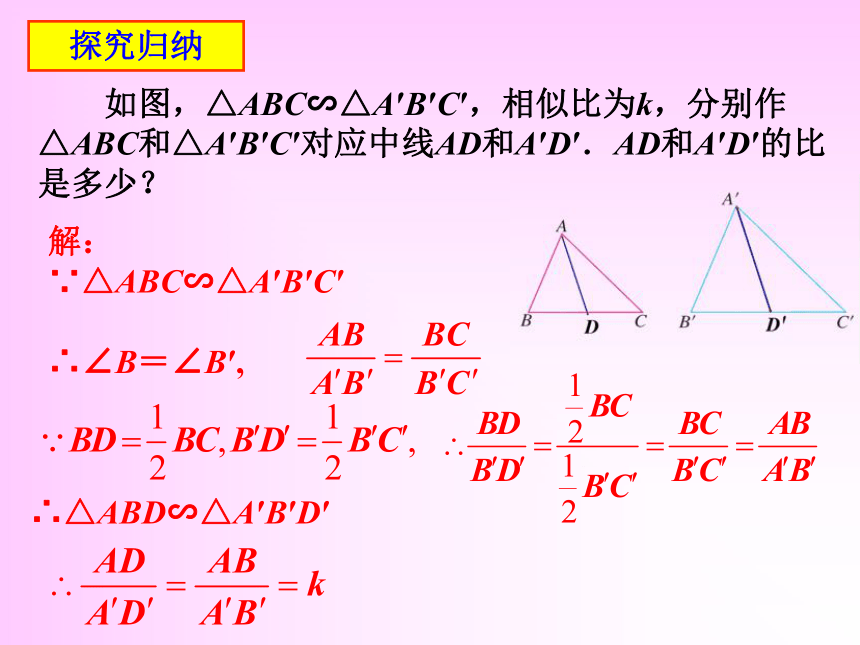
它们相似吗?如何证明?探究归纳 探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?对应高的比等于相似比k它们的对应中线是否也等于相似比k? 探究归纳 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少? 解:
∵△ABC∽△A′B′C′
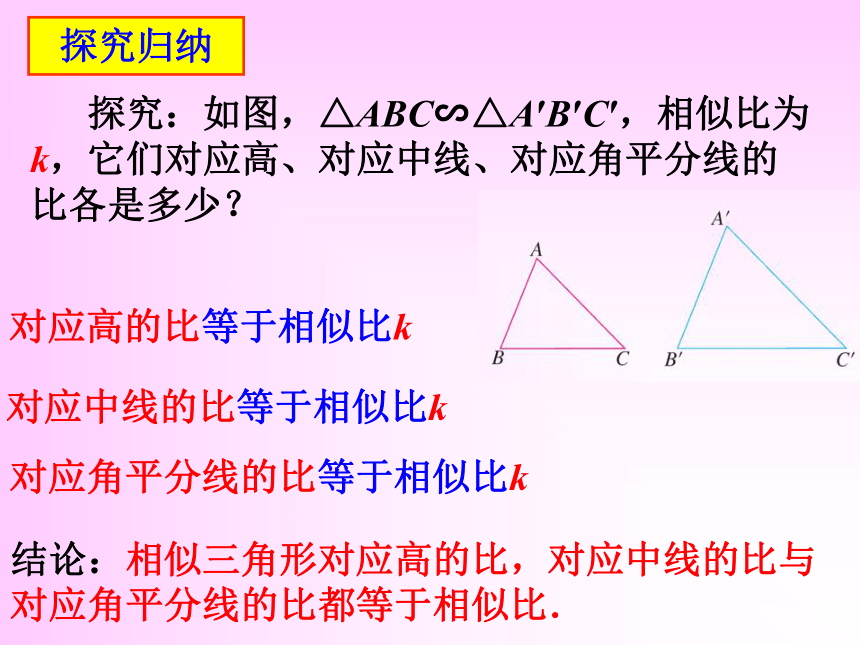
∴∠B=∠B′,∴△ABD∽△A′B′D′探究归纳 探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?对应高的比等于相似比k对应中线的比等于相似比k对应角平分线的比等于相似比k结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.探究归纳 问题:如果△ABC∽△A′B′C′,相似比为k,对应线段的比呢?推广:相似三角形对应线段的比等于相似比. 对应边的比相似比k对应高的比对应中线的比对应角平分线的比……=结论:相似三角形的周长比等于相似比.探究归纳 思考:相似三角形面积比与相似比有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.结论:相似三角形面积比等于相似比的平方.例:如图,△ABC∽△A′B′C′,它们的周长分别为60和72,且AB=15,B′C′=24,求BC、AC、A′B′、A′C′的长.解: ∵△ABC∽△A′B′C′应用提高练习:如图,在△ABC 和△DEF 中,AB=2DE,
AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是6,面积为 ,求△DEF 的边 EF上的高和面积. 解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,∵∠A=∠D,
∴△DEF∽△ABC,△DEF与△ABC的相似比为∵△ABC 的边 BC 上的高是6,面积为 ,
∴△DEF的边 EF 上的高为
面积为 应用提高1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )√×应用提高 2.在一张复印出来的纸上,一个三角形的一条边由原来的2cm变成了6cm,放缩比例是多少?这个三角形的面积发生了怎样的变化? ∴放缩比例是300%解:∵6:2=3∵32=9∴面积扩大为原来的9倍 设两个三角形的面积分别是4x,9x,根据题意得:拓展提升 1.两个相似三角形的周长之比是2:3,它们的面积之差是60cm2 ,那么它们的面积之和是多少?解得 x=12,9x﹣4x=60 ∴它们的面积之比是4:9.解:∵两个三角形的周长之比是2:3,
∴它们的相似比是2:3,∴9x+4x=156答:它们的面积之和是156cm2.拓展提升 2.如图,这是比例尺为1:1000的一块三角形草坪的图形,则草坪的实际面积是多少?∴它们的面积之比是
1:1000000.解:∵比例尺为1:1000,∵图上草坪面积为:∴草坪面积实际面积为:(cm2)3×1000000=3000000(cm2)=300(cm2)拓展提升 3.如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积. (1)△ADE 的周长是32,面积16.(2)△ EFC 的面积36.四边形 DBFE 的面积48. 课内检测 1.用放大镜看一个三角形,一条边由原来的1cm变成5cm,那么看到的图案面积是原来的( )
A.5倍 B.15倍 C.25倍 D.30倍
2.两个等腰直角三角形的斜边比为1:2,则它们的周长比为( )
A.1:1 B.1:2 C.1:4 D.1:
3. 两个相似三角形最长边分别是20cm和16cm,它们的周长之和为90cm,则较大三角形的周长为( )
A.40cm B.50 cm C.60 cm D.70 cmCBB课内检测 4.两个相似三角的对应高分别为6cm和4cm,则这两个三角形的周长比为________,面积比为________.
5.已知两个相似三角形面积之比为9:25,其中一个周长为36,则另一个的周长为____________.3:29:460或21.6体验收获 说一说你的收获 ……1.相似三角形对应角相等,
对应边成比例(对应边的比等于相似比)
2.相似三角形对应高线、对应中线、对应角平分线的比等于相似比
推广:相似三角形对应线段的比等于相似比
3.相似三角形对应周长比等于相似比
4.相似三角形对应面积比等于相似比的平方
∴∠B=∠B′
∵△ABD和△A′B′D′都是直角三角形
∴△ABD∽△A′B′D′ 对应高在哪两个三角形中,
它们相似吗?如何证明?探究归纳 探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?对应高的比等于相似比k它们的对应中线是否也等于相似比k? 探究归纳 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少? 解:
∵△ABC∽△A′B′C′
∴∠B=∠B′,∴△ABD∽△A′B′D′探究归纳 探究:如图,△ABC∽△A′B′C′,相似比为k,它们对应高、对应中线、对应角平分线的比各是多少?对应高的比等于相似比k对应中线的比等于相似比k对应角平分线的比等于相似比k结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.探究归纳 问题:如果△ABC∽△A′B′C′,相似比为k,对应线段的比呢?推广:相似三角形对应线段的比等于相似比. 对应边的比相似比k对应高的比对应中线的比对应角平分线的比……=结论:相似三角形的周长比等于相似比.探究归纳 思考:相似三角形面积比与相似比有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.结论:相似三角形面积比等于相似比的平方.例:如图,△ABC∽△A′B′C′,它们的周长分别为60和72,且AB=15,B′C′=24,求BC、AC、A′B′、A′C′的长.解: ∵△ABC∽△A′B′C′应用提高练习:如图,在△ABC 和△DEF 中,AB=2DE,
AC=2DF,∠A=∠D.若△ABC 的边 BC 上的高是6,面积为 ,求△DEF 的边 EF上的高和面积. 解:在△ABC 和△DEF 中,
∵AB=2DE,AC=2DF,∵∠A=∠D,
∴△DEF∽△ABC,△DEF与△ABC的相似比为∵△ABC 的边 BC 上的高是6,面积为 ,
∴△DEF的边 EF 上的高为
面积为 应用提高1.判断
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的角平分线也扩大为原来的5倍; ( )
(2)一个三角形的各边长扩大为原来的9倍,这个三角形的面积也扩大为原来的9倍. ( )√×应用提高 2.在一张复印出来的纸上,一个三角形的一条边由原来的2cm变成了6cm,放缩比例是多少?这个三角形的面积发生了怎样的变化? ∴放缩比例是300%解:∵6:2=3∵32=9∴面积扩大为原来的9倍 设两个三角形的面积分别是4x,9x,根据题意得:拓展提升 1.两个相似三角形的周长之比是2:3,它们的面积之差是60cm2 ,那么它们的面积之和是多少?解得 x=12,9x﹣4x=60 ∴它们的面积之比是4:9.解:∵两个三角形的周长之比是2:3,
∴它们的相似比是2:3,∴9x+4x=156答:它们的面积之和是156cm2.拓展提升 2.如图,这是比例尺为1:1000的一块三角形草坪的图形,则草坪的实际面积是多少?∴它们的面积之比是
1:1000000.解:∵比例尺为1:1000,∵图上草坪面积为:∴草坪面积实际面积为:(cm2)3×1000000=3000000(cm2)=300(cm2)拓展提升 3.如图,△ABC 的面积为 100,周长为 80,AB=20,点 D 是 AB 上一点,BD=12,过点 D 作 DE∥BC,交 AC于点 E.(1)求△ADE 的周长和面积;(2)过点 E 作 EF∥AB,EF 交 BC 于点 F,求△EFC 和四边形 DBFE 的面积. (1)△ADE 的周长是32,面积16.(2)△ EFC 的面积36.四边形 DBFE 的面积48. 课内检测 1.用放大镜看一个三角形,一条边由原来的1cm变成5cm,那么看到的图案面积是原来的( )
A.5倍 B.15倍 C.25倍 D.30倍
2.两个等腰直角三角形的斜边比为1:2,则它们的周长比为( )
A.1:1 B.1:2 C.1:4 D.1:
3. 两个相似三角形最长边分别是20cm和16cm,它们的周长之和为90cm,则较大三角形的周长为( )
A.40cm B.50 cm C.60 cm D.70 cmCBB课内检测 4.两个相似三角的对应高分别为6cm和4cm,则这两个三角形的周长比为________,面积比为________.
5.已知两个相似三角形面积之比为9:25,其中一个周长为36,则另一个的周长为____________.3:29:460或21.6体验收获 说一说你的收获 ……1.相似三角形对应角相等,
对应边成比例(对应边的比等于相似比)
2.相似三角形对应高线、对应中线、对应角平分线的比等于相似比
推广:相似三角形对应线段的比等于相似比
3.相似三角形对应周长比等于相似比
4.相似三角形对应面积比等于相似比的平方
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
