18.6 相似三角形的性质 课件(17张PPT)
文档属性
| 名称 | 18.6 相似三角形的性质 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 350.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 11:36:34 | ||
图片预览




文档简介
课件17张PPT。相似三角形的性质(1)平行法:
(2)判定定理:①边边边
②边角边
③角角
④斜边、直角边1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?对应角相等
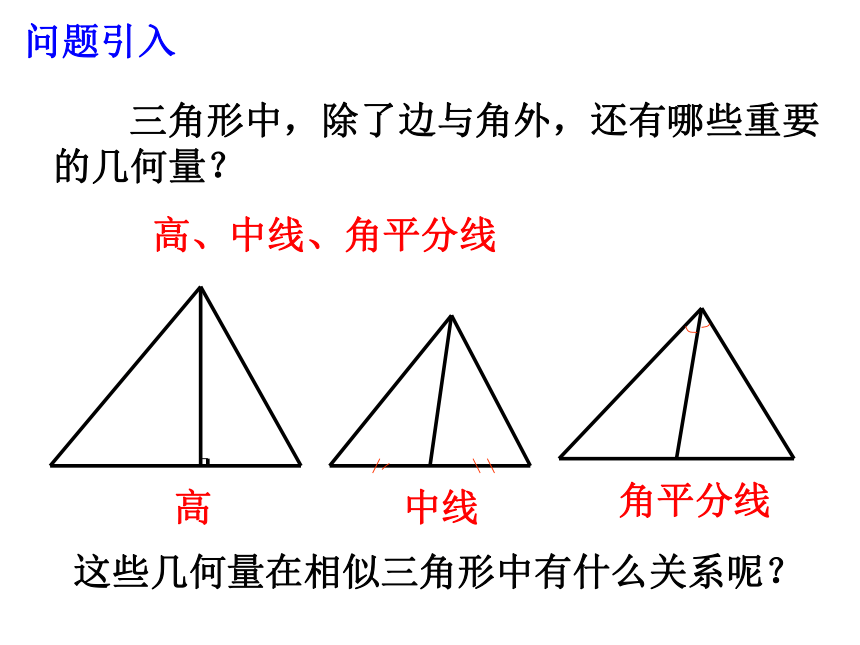
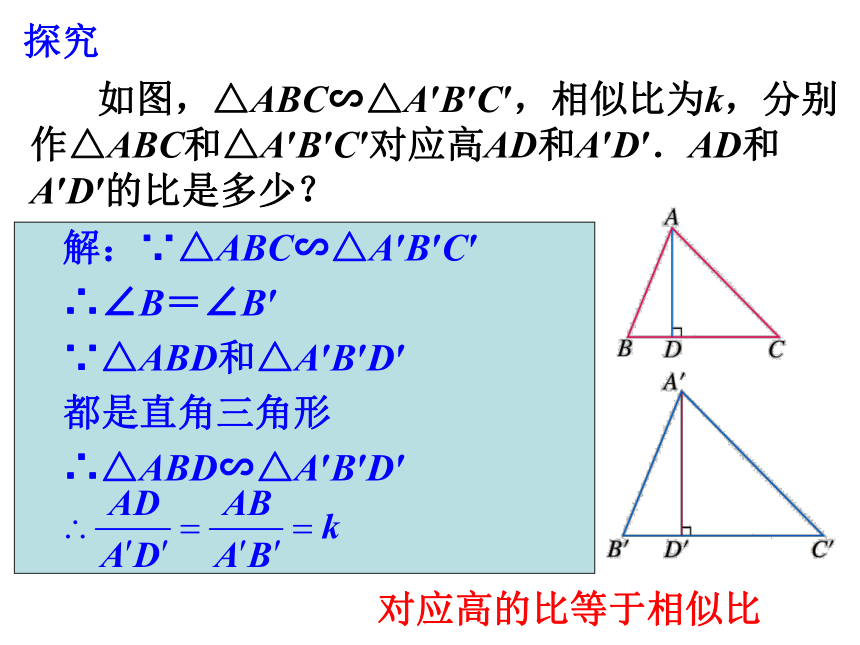
对应边成比例复习提问 三角形中,除了边与角外,还有哪些重要的几何量?高、中线、角平分线问题引入这些几何量在相似三角形中有什么关系呢?探究 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′
都是直角三角形
∴△ABD∽△A′B′D′对应高的比等于相似比探究对应中线的比等于相似比 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′,∴△ABD∽△A′B′D′探究 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应角平分线AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
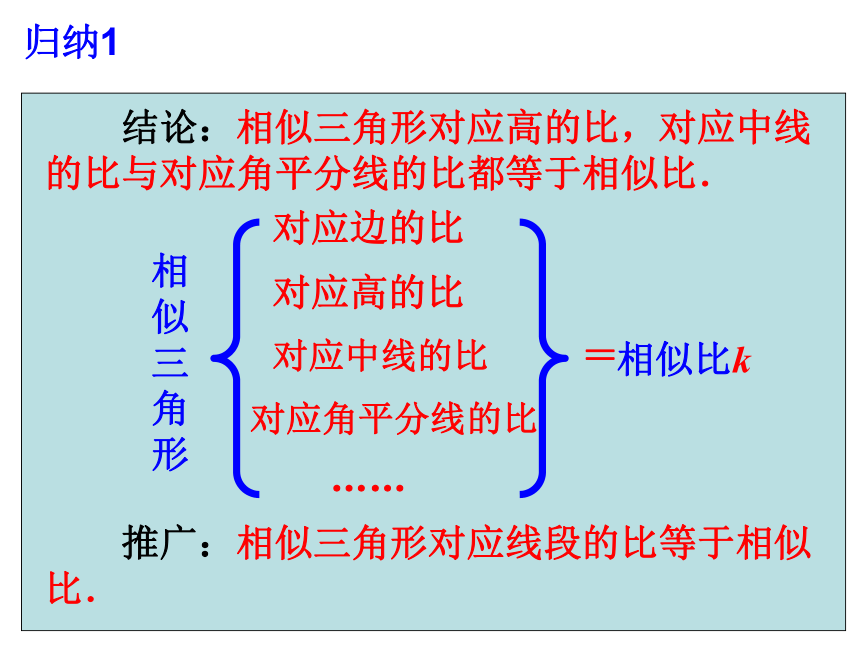
∴∠B=∠B′, ∴∠BAC=∠B′A′C′∴△ABD∽△A′B′D′对应角平分线的比等于相似比归纳1 结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.对应边的比相似比k对应高的比对应中线的比对应角平分线的比=相似三角形…… 推广:相似三角形对应线段的比等于相似比. (3)如图,DE∥BC,AG⊥BC于G,DE=2,BC=6,AF=1,则AG=_____.(2)两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A.7∶3 B.49∶9 C.9∶49 D.3∶7(1)已知△ABC与△ A′B′C′的相似比为2:3,则对应边上中线之比 ,对应高的比为
,对应角平分线的比为 .2:32:32:3D3练习1思考1相似三角形的周长有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,它们的周长比是多少? 解∵△ABC∽△A′B′C′
且相似比为k,相似三角形周长比等于相似比思考2相似三角形面积的比与相似比有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,它们的面积比与相似比有什么关系? 相似三角形面积比等于相似比的平方. 解:分别作△ABC和△A′B′C′对应高AD和A′D′.归纳2相似三角形周长比等于相似比相似三角形面积比等于相似比的平方.推论:相似多边形的周长比等于相似比,
面积比等于相似比的平方.例:如图,△ABC∽△A′B′C′,它们的周长分别为60和72,且AB=15,B′C′=24,求BC、AC、A′B′、A′C′的长.解: ∵△ABC∽△A′B′C′(1)已知△ABC与△ A′B′C′ 的相似比为3:4,则对应边上中线之比 ,周长比为
,面积之比为 .
(2)已知△ ABC∽ △ A′B′C′,且面积之比为25:9,则相似比 ,周长之比为 . 3:49:163:4练习2 2.在△ABC中,D 、E分别是AB,AC上的点,且DE∥BC,DE=4,BC=12,则△ADE与四边形BCED的面积比为________.拓展提升 1.两个相似三角形的对应角平分线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长为______cm,
面积为______ cm2.1441:8拓展提升 3.如图所示,D、E分别是AC、AB上的点,
,已知△ABC的面积为100cm2,求四边形BCDE的面积.解:∵ ,∠A=∠A∴∵∴△ADE∽△ABC∴∴拓展提升 4.在建设施工中,曾遇到这样一个实际问题:
由于马路拓宽,有一个面积是100m2、周长80m的三角形的绿化地被削去了一个角,变成了一块梯形绿地,原绿化地的一边AB的长由原来的20m缩短成12m(如图所示).为了保证绿化建设,市政府要求:因为种种原因而失去的绿地面积必须等面积补回.那么这块失去的面积到底有多大?它的周长是多少?周长是32m面积是16m2谈谈你今天的收获相似三角形的性质对应角相等对应边成比例对应高的比,对应中线的比、对应角平分线的比等于相似比.周长比等于相似比面积比等于相似比的平方对应线段的比等于相似比. 推论:相似多边形的周长比等于相似比,
面积比等于相似比的平方.
(2)判定定理:①边边边
②边角边
③角角
④斜边、直角边1、判断两三角形相似有哪些方法?2、相似三角形有什么性质?对应角相等
对应边成比例复习提问 三角形中,除了边与角外,还有哪些重要的几何量?高、中线、角平分线问题引入这些几何量在相似三角形中有什么关系呢?探究 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应高AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′
∵△ABD和△A′B′D′
都是直角三角形
∴△ABD∽△A′B′D′对应高的比等于相似比探究对应中线的比等于相似比 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应中线AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′,∴△ABD∽△A′B′D′探究 如图,△ABC∽△A′B′C′,相似比为k,分别作△ABC和△A′B′C′对应角平分线AD和A′D′.AD和A′D′的比是多少? 解:∵△ABC∽△A′B′C′
∴∠B=∠B′, ∴∠BAC=∠B′A′C′∴△ABD∽△A′B′D′对应角平分线的比等于相似比归纳1 结论:相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.对应边的比相似比k对应高的比对应中线的比对应角平分线的比=相似三角形…… 推广:相似三角形对应线段的比等于相似比. (3)如图,DE∥BC,AG⊥BC于G,DE=2,BC=6,AF=1,则AG=_____.(2)两个相似三角形对应高的比为3∶7,它们的对应角平分线的比为( )
A.7∶3 B.49∶9 C.9∶49 D.3∶7(1)已知△ABC与△ A′B′C′的相似比为2:3,则对应边上中线之比 ,对应高的比为
,对应角平分线的比为 .2:32:32:3D3练习1思考1相似三角形的周长有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,它们的周长比是多少? 解∵△ABC∽△A′B′C′
且相似比为k,相似三角形周长比等于相似比思考2相似三角形面积的比与相似比有什么关系? 如图,△ABC∽△A′B′C′,相似比为k,它们的面积比与相似比有什么关系? 相似三角形面积比等于相似比的平方. 解:分别作△ABC和△A′B′C′对应高AD和A′D′.归纳2相似三角形周长比等于相似比相似三角形面积比等于相似比的平方.推论:相似多边形的周长比等于相似比,
面积比等于相似比的平方.例:如图,△ABC∽△A′B′C′,它们的周长分别为60和72,且AB=15,B′C′=24,求BC、AC、A′B′、A′C′的长.解: ∵△ABC∽△A′B′C′(1)已知△ABC与△ A′B′C′ 的相似比为3:4,则对应边上中线之比 ,周长比为
,面积之比为 .
(2)已知△ ABC∽ △ A′B′C′,且面积之比为25:9,则相似比 ,周长之比为 . 3:49:163:4练习2 2.在△ABC中,D 、E分别是AB,AC上的点,且DE∥BC,DE=4,BC=12,则△ADE与四边形BCED的面积比为________.拓展提升 1.两个相似三角形的对应角平分线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长为______cm,
面积为______ cm2.1441:8拓展提升 3.如图所示,D、E分别是AC、AB上的点,
,已知△ABC的面积为100cm2,求四边形BCDE的面积.解:∵ ,∠A=∠A∴∵∴△ADE∽△ABC∴∴拓展提升 4.在建设施工中,曾遇到这样一个实际问题:
由于马路拓宽,有一个面积是100m2、周长80m的三角形的绿化地被削去了一个角,变成了一块梯形绿地,原绿化地的一边AB的长由原来的20m缩短成12m(如图所示).为了保证绿化建设,市政府要求:因为种种原因而失去的绿地面积必须等面积补回.那么这块失去的面积到底有多大?它的周长是多少?周长是32m面积是16m2谈谈你今天的收获相似三角形的性质对应角相等对应边成比例对应高的比,对应中线的比、对应角平分线的比等于相似比.周长比等于相似比面积比等于相似比的平方对应线段的比等于相似比. 推论:相似多边形的周长比等于相似比,
面积比等于相似比的平方.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
