19.2 二次函数y=ax2 bx c(a≠0)的图象 教案(4课时)
文档属性
| 名称 | 19.2 二次函数y=ax2 bx c(a≠0)的图象 教案(4课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 148.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 11:39:31 | ||
图片预览




文档简介
《二次函数y=ax2+bx+c(a≠0)的图象》教案
第一课时
教学目标
知识与技能
1.能正确画出二次函数y=x2和y=-x2的图象,探究出二次函数的图象的形状;
2.理解二次函数y=x2和y=-x2中y随x的变化规律及二次函数图象的对称性;
3.掌握二次函数y=x2和y=-x2图象的开口方向、对称轴、顶点坐标;
4.通过操作、探究的过程,提高学生对知识的理解和应用能力.
过程与方法
1.通过动手操作画二次函数y=x2和y=-x2的图象,发展几何直观,培养学生的动手能力,掌握其操作方法和技巧;
2.通过对二次函数y=x2和y=-x2图象的探究,理解这种形式的二次函数的特征,掌握解题的方法和技巧.
情感、态度与价值观
经过操作、探究、总结和应用等数学活动,让学生感受数学中数形变化美,让学生感受到数学的严谨性和科学性,让学生感受到数学的应用在生活中无处不在.
教学重点与难点
重点:使学生会画二次函数y=x2和y=-x2的图象,能概括它们的性质.
难点:理解并把握二次函数y=x2和y=-x2的图象的形状和性质特征.
教学过程
一、知识回顾,导入新课
问题1:什么叫做二次函数?
生:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
问题2:画函数图象的主要步骤是什么?
生:(1)列表,(2)描点,(3)连线
问题3:你能说说我们已经学习过的一次函数有哪些性质吗?
生:一次函数y=kx+b(k,b都是常数,且k≠0)中,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.
思考:在二次函数y=x2中,y随x的变化而变化的规律是什么?你想直观地了解它的性质吗?
二、探究交流,获取新知
操作:请你画出二次函数y=x2的图象.
(1)观察y=x2的表达式,选择适当的x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y
…
9
4
1
0
1
4
9
…
(2)在直角坐标系中描点:
(3)用光滑的曲线连接各点,便得到函数y=x2的图象.
议一议:
对于二次函数y=x2的图象.
(1)你能描述图象的形状吗?与同伴进行交流.
生:抛物线.
(2)图象与x轴有交点吗?如果有,交点坐标是什么?
生:图象与x轴有交点.交点坐标是(0,0).
(3)当x取什么值时,y的值最小?
最小值是什么?你是如何知道的?
生:当x=0时,y的值最小,最小值是0.
因为抛物线上的最低点坐标是(0,0).
(4)图象是轴对称图形吗?如果是,它的对称轴是什么?
请你找出几对对称点,并与同伴进行交流.
生:图象是轴对称图形.它的对称轴是y轴.
对称点:(-3,9)与(3,9)关于y轴对称;(-2,4)与(2,4)关于y轴对称……
师生共同总结:1.函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称.
2.对称轴与抛物线的交点是抛物线的顶点,它是图象的最低点.
做一做:
二次函数y=-x2的图象是什么形状?先想一想,然后作出它的图象,它与二次函数y=x2的图象有什么关系?与同伴进行交流.
(1)列表:
x
…
-3
-2
-1
0
1
2
3
…
y
…
-9
-4
-1
0
-1
-4
-9
…
(2)在直角坐标系中描点:
(3)用光滑的曲线连接各点,便得到函数y=-x2的图象.
议一议:说说二次函数y=-x2的图象有哪些性质,与同伴交流.
(1)图象与x轴交于原点(0,0).
(2)y≤0.
(3)当x=0时,y最大值=0.
(4)图象关于y轴对称.
例1 在同一坐标系中,做出下列函数的图象:
三、知识拓展
1.画出二次函数y=2x2的图象,根据图象回答下列问题:
(1)抛物线y=2x2的开口方向是怎样的?
(2)抛物线y=2x2顶点坐标、对称轴各是多少?
(3)函数y有最大值还是最小值?为什么?
四、自我小结,获取感悟
1.二次函数y=±x2的图象是什么形状?
2.二次函数y=±x2有哪些性质?
(1)位置与开口方向;
(2)顶点坐标与对称轴.
第二课时
教学目标
知识与技能
1.能正确画出二次函数y=ax2和y=ax2+c的图象,并会比较这两种二次函数的图象的不同点;
2.把握系数a、c对二次函数图象的影响,理解二次函数y=ax2和y=ax2+c中y随x的变化规律及抛物线的平移规律;
3.能说出二次函数y=ax2和y=ax2+c图象的开口方向、对称轴、顶点坐标;
4.通过操作、探究的过程,提高学生对基础知识的理解和运用能力.
过程与方法
1.通过动手操作画二次函数y=ax2和y=ax2+c的图象,培养学生的比较、鉴别能力;
2.通过对二次函数y=ax2和y=ax2+c图象的探究,理解这两种形式的二次函数的性质特征.
情感、态度与价值观
经过操作、探究、总结和应用等数学活动,有趣的实际问题,使学生能积极参与数学学习活动,对数学有好奇心和求知欲.
教学重点与难点
重点:使学生会画二次函数y=ax2和y=ax2+c的图象,并会进行比较异同,能根据图象概括出它们的性质特征.
难点:正确理解二次函数y=ax2和y=ax2+c的图象与系数的关系,能灵活运用其性质解决相关函数问题.
教学过程
一、知识回顾,导入新课
1.如图是二次函数y=x2和y=-x2的图象,填写下表:
函数
图象形状
开口方向
对称轴
顶点坐标
y=x2
抛物线
向上
y轴
(0,0)
y=-x2
抛物线
向下
y轴
(0,0)
2.画一画
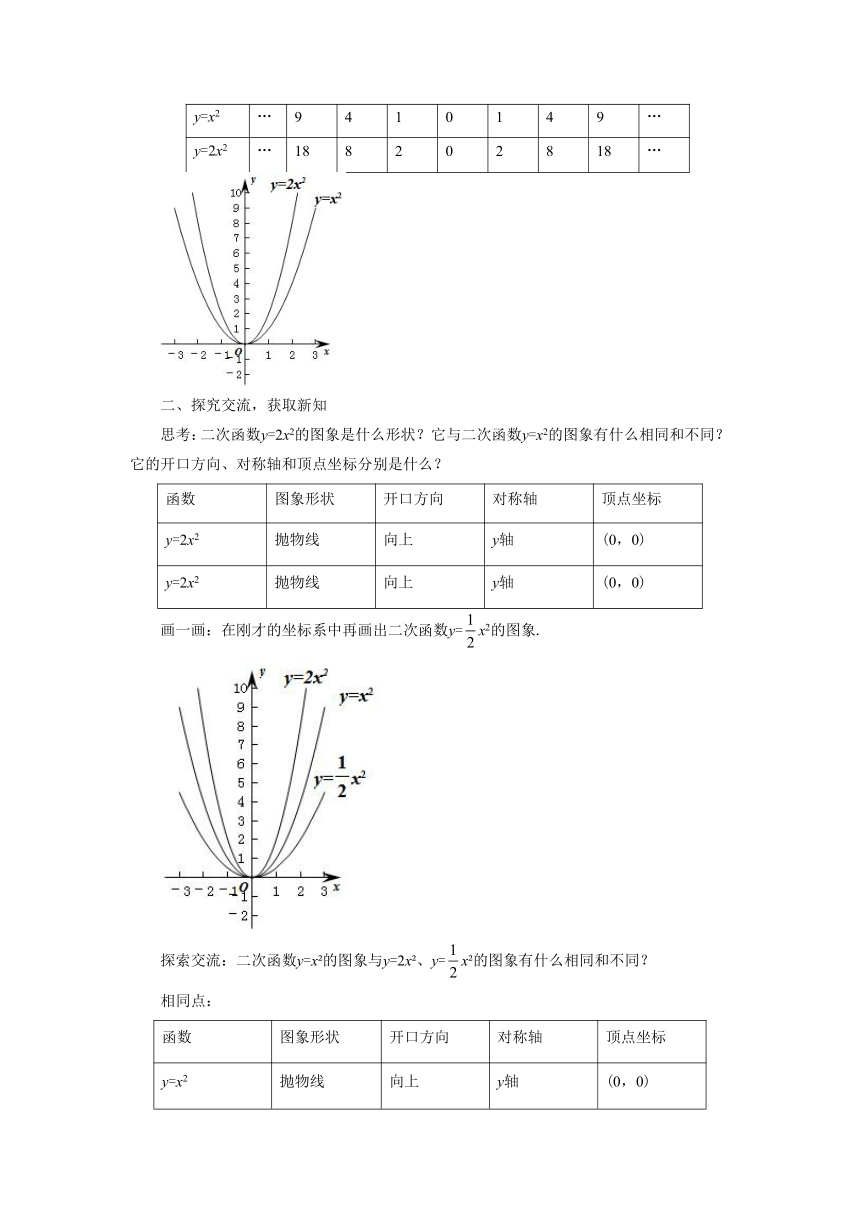
在同一坐标系中,画出二次函数y=x2和y=2x2,
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
y=2x2
…
18
8
2
0
2
8
18
…
二、探究交流,获取新知
思考:二次函数y=2x2的图象是什么形状?它与二次函数y=x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
函数
图象形状
开口方向
对称轴
顶点坐标
y=2x2
抛物线
向上
y轴
(0,0)
y=2x2
抛物线
向上
y轴
(0,0)
画一画:在刚才的坐标系中再画出二次函数y=x2的图象.
探索交流:二次函数y=x2的图象与y=2x2、y=x2的图象有什么相同和不同?
相同点:
函数
图象形状
开口方向
对称轴
顶点坐标
y=x2
抛物线
向上
y轴
(0,0)
y=2x2
抛物线
向上
y轴
(0,0)
y=x2
抛物线
向上
y轴
(0,0)
不同点:a的绝对值越大,抛物线的开口越小.
做一做:
在下列平面直角坐标系中,作出y=-x2和y=-2x2的图象.
生:动手操作画图,
思考:它们与二次函数y=x2和y=2x2的图象又有什么异同?
生:它们形状、对称轴和顶点坐标都是相同的,只是y=-x2和y=-2x2的图象开口向下.
探究:函数y=3x2及y=-3x2的图象会有哪些特点?
点拨:从二次函数的形状、开口方向、对称轴和顶点坐标几个方面回答.
师生共同总结:y=ax2 (a≠0)的图象与性质特征,
探究:二次函数y=2x2+2、y=2x2-2与二次函数y=2x2的图象有什么相同与不同?你是怎样想的,动手验证你的想法.
生:学生动手操作,老师巡视,
结论:1.二次函数y=2x2+2由二次函数y=2x2的图象向上平移2个单位;
2.二次函数y=2x2-2由二次函数y=2x2的图象向下平移2个单位.
共同交流:二次函数y=-3x2+, y=-3x2-的图象与二次函数y=-3x2的图象有什么关系?
生:让学生总结出它们之间的关系.
思考:二次函数y=ax2(a≠0)的图象与y=ax2+c(a≠0)的图象有什么异同?
老师点拨:y=ax2及y=ax2+c(a≠0)的图象和性质:
y=ax2+c的图象是由y=ax2的图象上下平移得到的,
当c>0时,向上平移c个单位;
当c<0时,向下平移︱c︱个单位.
函数
图象形状
开口方向
对称轴
顶点坐标
y=ax2
抛物线
a>0向上
a<0向下
y轴
(0,0)
y=ax2+c
抛物线
a>0向上
a<0向下
y轴
(0,c)
四、随堂练习
1.将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是( ).
A.y=-(x+2)2 B.y=-x2+2 C.y=-x2+2 D.y=-(x-2)2
2.在平面直角坐标系中,抛物线y=x2-1 与x轴的交点的个数是( )
A.3 B.2 C.1 D.0
3.坐标平面上有一函数y=24x2-48的图象,其顶点坐标为( )
A.(0,-2) B.(1,-24) C.(0,-48) D.(2,48)
4.将抛物线y=x2+1向下平移2个单位,则此时抛物线的解析式是________.
五、自我小结,获取感悟
1.对自己说,你在本节课中学习了哪些知识点?有何收获?
2.对同学说,你有哪些学习感悟和温馨提示?
3.对老师说,你还有哪些困惑?
第三课时
教学目标
知识与技能
1.能正确画出形如y=a(x-h)2和y=a(x-h)2+k的二次函数的图象,并能理解它与y=ax2的图象的关系,理解a、h、k对二次函数图象的影响;
2.能正确地说出y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标;
3.能灵活运用二次函数的图象和性质解决相关问题;
4.通过对知识点的探究以达到灵活运动知识解答相关问题的技能.
过程与方法
1.通过对二次函数y=a(x-h)2和y=a(x-h)2+k的图象的画法的操作,性质的探究,达到对抛物线自身特点的认识和对二次函数性质的理解;
2.经历探索二次函数的图象的作法和性质的过程,培养学生的探索能力.
情感、态度与价值观
1.经历观察、猜想、总结等数学活动过程,培养学生合情推理能力和初步的演绎推理能力,能在条理地、清晰地阐述自己的观点;
2.让学生学会与人合作,并能与他人进行交流思维的过程和结果.
教学重点与难点
重点:使学生能准确地作出这两种形式的二次函数图象,理解它们与y=ax2的图象关系,理解a、h、k对二次函数图象的影响,能正确说出y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标,准确把握二次函数的性质特点.
难点:理解并把握二次函数y=a(x-h)2和y=a(x-h)2+k的图象的性质特征,并会运用性质解决相关问题.
教学准备
多媒体课件.
教学过程
一、知识回顾,导入新课
问题1:根据你所学知识回答下列各问题,
1.函数y=x2+3的图象的顶点坐标是___________;开口方向是______;最_____值是________.
2.函数y=-2x2+3的图象可由函数_____________的图象向____平移_________个单位得到.
3.把函数y=-3x2的图象向下平移2个单位可得到函数_________________的图象.
问题2:你会用类比法画二次函数y=2(x-1)2的图象吗?它与y=2x2有什么异同吗?它有哪些性质呢?
二、探究交流,获取新知
请你在同一坐标系中画出下列函数的图象:
(1)y=2x2 (2)y=2(x-1)2
完成下表:
x
…
-4
-3
-2
-1
0
1
2
3
4
…
2x2
…
…
2(x-1)2
…
…
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
生:在同一坐标系中画出这两个函数图象,
议一议:(1)二次函数y=2(x-1)2的图象与y=22的图象有什么关系?
生:二次函数y=2(x-1)2的图象是由二次函数y=2x2的图象向右平移1个单位得到的.
(2)二次函数y=2(x-1)2的图象的开口方向、对称轴和顶点坐标分别是什么?
生:开口向上,对称轴为x=1,顶点坐标为(1,0)
(3)二次函数y=2(x-1)2当x取何值时,y的值随x值的增大而增大?当x取何值时,y的值随x值的增大而减小?
生:当x<1时,y的值随x值的增大而增大;当x>1时,y的值随x值的增大而减小.
(4)你能发现二次函数y=2(x-1)2的图象与二次函数y=2x2的图象有什么关系吗?
生:二次函数y=2(x-1)2的图象是由二次函数y=2x2的图象向左平移1个单位得到的.
结论:二次函数y=2x2,y=2(x-1)2,y=2(x+1)2的图象都是抛物线,并且形状相同,只是位置不同. 将函数y=2x2的图象向右平移1个单位长度,就得到函数y=2(x-1)2的图像;将函数y=2x2的图象向左平移1个单位长度,就得到函数y=2(x+1)2的图像.
想一想:由二次函数y=2x2的图象,你能得二次函数y=2x2-,y=2(x+3)2,y=2(x+3)2-的图象吗?
生:由二次函数y=2x2的图象向下平移个单位长度可得二次函数y=2x2-的图象;由二次函数y=2x2的图象向左平移3个单位长度能得二次函数y=2(x+3)2的图象;由二次函数y=2x2的图象先向左平移3个单位长度,再向下平移个单位长度,能得二次函数y=2(x-3)2-的图象.
归纳总结:二次函数y=a(x-h)2+k与二次函数y=ax2的图象有什么关系?
二次函数y=a(x-h)2+k的图象是由二次函数y=ax2的图象先向左(或向右)平移|h|个单位长度,再向上(或向下)平移|k|个单位长度得到的.
h<0时,图象向左平移;h>0时,图象向右平移.
k<0时,图象向下平移;k>0时,图象向上平移.
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象.因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标如下表所示:
开口方向
对称轴
顶点坐标
y=a(x-h)2+k
向上(a>0)
直线x=h
(0,0)
向下(a<0)
三、随堂练习
1.回答下列问题:
二次函数y=3(x+2)2的图象与二次函数y=-3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
2.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x-2)2+1 B.y=(x+2)2+1 C.y=(x-2)2-3 D.y=(x+2)2-3
3.将抛物线y=2(x-1)2向左平移1个单位后所得到的新抛物线的表达式为___________.
4.将抛物线y=-x2先向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式为____________.
5.若把函数y=x的图象用 E(x,x)记,函数y=2x+1的图象用 E(x,2x+1)记,…,则E(x,x2-2x+1)可以由 E(x,x2)怎样平移得到( )
A.向上平移1个单位 B.向下平移1个单位
C.向左平移1个单位 D.向右平移1个单位
例2 已知二次函数.
(1)指出它的图象可以看做是函数的图象经过怎样的变换而得到的;
(2)指出图象的开口方向、对称轴和顶点坐标;
(3)求出图象与坐标轴的交点坐标,并画出它的示意图.
六、自我小结,获取感悟
1.y=a(x-h)2+k的图象特征.
2.y=a(x-h)2+k的图象与y=ax2的图象的关系.
第四课时
教学目标
知识与技能
1.会用配方法将y=ax2+bx+c化成y=a(x-h)2+k形式,体会建立二次函数的对称轴和顶点坐标公式的必要性;
2.能够利用二次函数的对称轴和顶点坐标公式解决有关函数问题;
3.掌握系数a、b、c对二次函数图象的影响和作用;
4.通过操作、探究的过程,提高学生对知识的理解和把握能力.
过程与方法
1.通过对二次函数y=ax2+bx+c的图象和性质的探究,培养学生的概括能力,解决实际问题的能力;
2.通过学生的合作交流来解决函数问题,培养学生的合作交流能力.
情感、态度与价值观
1.经历将一些实际问题抽象为数学问题的过程,掌握数学的基础知识和基本技能,并能解决简单的问题;
2.初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点与难点
重点:使学生会运用二次函数的对称轴和顶点坐标公式解决实际问题.
难点:理解并把握数学问题与实际问题相联系的过程.
教学准备:
多媒体课件
教学过程
一、知识回顾,导入新课
问题1:二次函数y=-2(x-3)2+5的开口_______,对称轴是_________,顶点坐标是____.它是由二次函数y=-2x2先向_____平移____个单位长度,再向_____平移____个单位长度得到的.
问题2:对于二次函数y=a(x-h)2+k
(1)当a>0时,它的开口______,对称轴是___________,顶点坐标是__________________.
(2)当a<0时,它的开口________,对称轴是____________,顶点坐标是_________________.
问题3:我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质,你能研究二次函数y=2x2-4x+5的图象吗?
二、探究交流,获取新知
请你利用已学过的知识将二次函数y=2x2-4x+5化成y=a(x-h)2+k的形式.
解: y=2x2-4x+5
=2(x2-2x)+5
=2(x2-2x+1-1)+5
=2(x-1)2-2+5
=2(x-1)2+3
三、知识讲解
1.求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解析:要求二次函数y=2x2-8x+7图象的对称轴和顶点坐标. 只需将它化为y=a(x-h)2+k的形式.
解:y=2x2-8x+7
=2(x2-4x)+7
=2(x2-4x+4)-8+7
=2(x-2)2-1
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
做一做:
确定下列二次函数图象的对称轴和顶点坐标:
(1)y=3x2-6x+7 (2)y=2x2-12x+8
生:学生解答,教师巡视,发现问题即时解答.
2.求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
生:指点一名学生上黑板解答,教师点拨.
解:把二次函数y=ax2+bx+c的右边配方,得:
y=ax2+bx+c
=a(x2+x)+c
=a[x2+2·x+()2-()2]+c
=a(x+)2+
因此,二次函数y=ax2+bx+c图象的对称轴是直线 x=-,顶点坐标为(-,).
点拨:由此我们把此称之为求二次函数图象的对称轴和顶点坐标的公式
四、随堂练习
1.用配方法确定下列函数的对称轴和顶点坐标
(1)y=2x2-12x+3; (2)y=-5x2+80x-319;
(3)y=2(x-)(x-2); (4)y=3(2x+1)(2-x).
合作交流:二次函数图象与系数a、b、c之间有何关系?
a决定抛物线的形状、开口方向.
当a>0时,抛物线开口向上,当a<0时,抛物线开口向下,越大抛物线的开口越小.
b影响对称轴的位置.
当ab>0时,抛物线的对称轴在y轴的左侧;当b=0时,抛物线的对称轴是y轴,当ab<0时,抛物线的对称轴在y轴的右侧.
c确定抛物线与y轴的交点位置.
当c>0时,抛物线与y轴的交点在y轴的正半轴上,当c=0时,抛物线经过坐标原点,当c<0时,抛物线与y轴的交点在y轴的负半轴上
例3 已知:抛物线y=-3x2+12x-8.(1)求出它的对称轴和顶点坐标;(2)求出图象与坐标轴的交点坐标,并画出示意图.
例4 已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
五、挑战自我:
1.(2014?遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. B. C. D.
2.若一次函数y=x2-2x+c的图象与y轴的交为(0,-3),则此二次函数有( )
A.最小值-2 B.最小值-3 C.最小值-4 D.最大值-4
六、自我小结,获取感悟
1.对自己说,你在本节课中学习了哪些知识点?有何收获?
2.对同学说,你有哪些学习感悟和温馨提示?
3.对老师说,你还有哪些困惑?
第一课时
教学目标
知识与技能
1.能正确画出二次函数y=x2和y=-x2的图象,探究出二次函数的图象的形状;
2.理解二次函数y=x2和y=-x2中y随x的变化规律及二次函数图象的对称性;
3.掌握二次函数y=x2和y=-x2图象的开口方向、对称轴、顶点坐标;
4.通过操作、探究的过程,提高学生对知识的理解和应用能力.
过程与方法
1.通过动手操作画二次函数y=x2和y=-x2的图象,发展几何直观,培养学生的动手能力,掌握其操作方法和技巧;
2.通过对二次函数y=x2和y=-x2图象的探究,理解这种形式的二次函数的特征,掌握解题的方法和技巧.
情感、态度与价值观
经过操作、探究、总结和应用等数学活动,让学生感受数学中数形变化美,让学生感受到数学的严谨性和科学性,让学生感受到数学的应用在生活中无处不在.
教学重点与难点
重点:使学生会画二次函数y=x2和y=-x2的图象,能概括它们的性质.
难点:理解并把握二次函数y=x2和y=-x2的图象的形状和性质特征.
教学过程
一、知识回顾,导入新课
问题1:什么叫做二次函数?
生:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.
问题2:画函数图象的主要步骤是什么?
生:(1)列表,(2)描点,(3)连线
问题3:你能说说我们已经学习过的一次函数有哪些性质吗?
生:一次函数y=kx+b(k,b都是常数,且k≠0)中,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.
思考:在二次函数y=x2中,y随x的变化而变化的规律是什么?你想直观地了解它的性质吗?
二、探究交流,获取新知
操作:请你画出二次函数y=x2的图象.
(1)观察y=x2的表达式,选择适当的x值,并计算相应的y值,完成下表:
x
…
-3
-2
-1
0
1
2
3
…
y
…
9
4
1
0
1
4
9
…
(2)在直角坐标系中描点:
(3)用光滑的曲线连接各点,便得到函数y=x2的图象.
议一议:
对于二次函数y=x2的图象.
(1)你能描述图象的形状吗?与同伴进行交流.
生:抛物线.
(2)图象与x轴有交点吗?如果有,交点坐标是什么?
生:图象与x轴有交点.交点坐标是(0,0).
(3)当x取什么值时,y的值最小?
最小值是什么?你是如何知道的?
生:当x=0时,y的值最小,最小值是0.
因为抛物线上的最低点坐标是(0,0).
(4)图象是轴对称图形吗?如果是,它的对称轴是什么?
请你找出几对对称点,并与同伴进行交流.
生:图象是轴对称图形.它的对称轴是y轴.
对称点:(-3,9)与(3,9)关于y轴对称;(-2,4)与(2,4)关于y轴对称……
师生共同总结:1.函数y=x2的图象是一条抛物线,它的开口向上,且关于y轴对称.
2.对称轴与抛物线的交点是抛物线的顶点,它是图象的最低点.
做一做:
二次函数y=-x2的图象是什么形状?先想一想,然后作出它的图象,它与二次函数y=x2的图象有什么关系?与同伴进行交流.
(1)列表:
x
…
-3
-2
-1
0
1
2
3
…
y
…
-9
-4
-1
0
-1
-4
-9
…
(2)在直角坐标系中描点:
(3)用光滑的曲线连接各点,便得到函数y=-x2的图象.
议一议:说说二次函数y=-x2的图象有哪些性质,与同伴交流.
(1)图象与x轴交于原点(0,0).
(2)y≤0.
(3)当x=0时,y最大值=0.
(4)图象关于y轴对称.
例1 在同一坐标系中,做出下列函数的图象:
三、知识拓展
1.画出二次函数y=2x2的图象,根据图象回答下列问题:
(1)抛物线y=2x2的开口方向是怎样的?
(2)抛物线y=2x2顶点坐标、对称轴各是多少?
(3)函数y有最大值还是最小值?为什么?
四、自我小结,获取感悟
1.二次函数y=±x2的图象是什么形状?
2.二次函数y=±x2有哪些性质?
(1)位置与开口方向;
(2)顶点坐标与对称轴.
第二课时
教学目标
知识与技能
1.能正确画出二次函数y=ax2和y=ax2+c的图象,并会比较这两种二次函数的图象的不同点;
2.把握系数a、c对二次函数图象的影响,理解二次函数y=ax2和y=ax2+c中y随x的变化规律及抛物线的平移规律;
3.能说出二次函数y=ax2和y=ax2+c图象的开口方向、对称轴、顶点坐标;
4.通过操作、探究的过程,提高学生对基础知识的理解和运用能力.
过程与方法
1.通过动手操作画二次函数y=ax2和y=ax2+c的图象,培养学生的比较、鉴别能力;
2.通过对二次函数y=ax2和y=ax2+c图象的探究,理解这两种形式的二次函数的性质特征.
情感、态度与价值观
经过操作、探究、总结和应用等数学活动,有趣的实际问题,使学生能积极参与数学学习活动,对数学有好奇心和求知欲.
教学重点与难点
重点:使学生会画二次函数y=ax2和y=ax2+c的图象,并会进行比较异同,能根据图象概括出它们的性质特征.
难点:正确理解二次函数y=ax2和y=ax2+c的图象与系数的关系,能灵活运用其性质解决相关函数问题.
教学过程
一、知识回顾,导入新课
1.如图是二次函数y=x2和y=-x2的图象,填写下表:
函数
图象形状
开口方向
对称轴
顶点坐标
y=x2
抛物线
向上
y轴
(0,0)
y=-x2
抛物线
向下
y轴
(0,0)
2.画一画
在同一坐标系中,画出二次函数y=x2和y=2x2,
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
9
4
1
0
1
4
9
…
y=2x2
…
18
8
2
0
2
8
18
…
二、探究交流,获取新知
思考:二次函数y=2x2的图象是什么形状?它与二次函数y=x2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?
函数
图象形状
开口方向
对称轴
顶点坐标
y=2x2
抛物线
向上
y轴
(0,0)
y=2x2
抛物线
向上
y轴
(0,0)
画一画:在刚才的坐标系中再画出二次函数y=x2的图象.
探索交流:二次函数y=x2的图象与y=2x2、y=x2的图象有什么相同和不同?
相同点:
函数
图象形状
开口方向
对称轴
顶点坐标
y=x2
抛物线
向上
y轴
(0,0)
y=2x2
抛物线
向上
y轴
(0,0)
y=x2
抛物线
向上
y轴
(0,0)
不同点:a的绝对值越大,抛物线的开口越小.
做一做:
在下列平面直角坐标系中,作出y=-x2和y=-2x2的图象.
生:动手操作画图,
思考:它们与二次函数y=x2和y=2x2的图象又有什么异同?
生:它们形状、对称轴和顶点坐标都是相同的,只是y=-x2和y=-2x2的图象开口向下.
探究:函数y=3x2及y=-3x2的图象会有哪些特点?
点拨:从二次函数的形状、开口方向、对称轴和顶点坐标几个方面回答.
师生共同总结:y=ax2 (a≠0)的图象与性质特征,
探究:二次函数y=2x2+2、y=2x2-2与二次函数y=2x2的图象有什么相同与不同?你是怎样想的,动手验证你的想法.
生:学生动手操作,老师巡视,
结论:1.二次函数y=2x2+2由二次函数y=2x2的图象向上平移2个单位;
2.二次函数y=2x2-2由二次函数y=2x2的图象向下平移2个单位.
共同交流:二次函数y=-3x2+, y=-3x2-的图象与二次函数y=-3x2的图象有什么关系?
生:让学生总结出它们之间的关系.
思考:二次函数y=ax2(a≠0)的图象与y=ax2+c(a≠0)的图象有什么异同?
老师点拨:y=ax2及y=ax2+c(a≠0)的图象和性质:
y=ax2+c的图象是由y=ax2的图象上下平移得到的,
当c>0时,向上平移c个单位;
当c<0时,向下平移︱c︱个单位.
函数
图象形状
开口方向
对称轴
顶点坐标
y=ax2
抛物线
a>0向上
a<0向下
y轴
(0,0)
y=ax2+c
抛物线
a>0向上
a<0向下
y轴
(0,c)
四、随堂练习
1.将抛物线y=-x2向左平移2个单位后,得到的抛物线的解析式是( ).
A.y=-(x+2)2 B.y=-x2+2 C.y=-x2+2 D.y=-(x-2)2
2.在平面直角坐标系中,抛物线y=x2-1 与x轴的交点的个数是( )
A.3 B.2 C.1 D.0
3.坐标平面上有一函数y=24x2-48的图象,其顶点坐标为( )
A.(0,-2) B.(1,-24) C.(0,-48) D.(2,48)
4.将抛物线y=x2+1向下平移2个单位,则此时抛物线的解析式是________.
五、自我小结,获取感悟
1.对自己说,你在本节课中学习了哪些知识点?有何收获?
2.对同学说,你有哪些学习感悟和温馨提示?
3.对老师说,你还有哪些困惑?
第三课时
教学目标
知识与技能
1.能正确画出形如y=a(x-h)2和y=a(x-h)2+k的二次函数的图象,并能理解它与y=ax2的图象的关系,理解a、h、k对二次函数图象的影响;
2.能正确地说出y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标;
3.能灵活运用二次函数的图象和性质解决相关问题;
4.通过对知识点的探究以达到灵活运动知识解答相关问题的技能.
过程与方法
1.通过对二次函数y=a(x-h)2和y=a(x-h)2+k的图象的画法的操作,性质的探究,达到对抛物线自身特点的认识和对二次函数性质的理解;
2.经历探索二次函数的图象的作法和性质的过程,培养学生的探索能力.
情感、态度与价值观
1.经历观察、猜想、总结等数学活动过程,培养学生合情推理能力和初步的演绎推理能力,能在条理地、清晰地阐述自己的观点;
2.让学生学会与人合作,并能与他人进行交流思维的过程和结果.
教学重点与难点
重点:使学生能准确地作出这两种形式的二次函数图象,理解它们与y=ax2的图象关系,理解a、h、k对二次函数图象的影响,能正确说出y=a(x-h)2+k图象的开口方向、对称轴和顶点坐标,准确把握二次函数的性质特点.
难点:理解并把握二次函数y=a(x-h)2和y=a(x-h)2+k的图象的性质特征,并会运用性质解决相关问题.
教学准备
多媒体课件.
教学过程
一、知识回顾,导入新课
问题1:根据你所学知识回答下列各问题,
1.函数y=x2+3的图象的顶点坐标是___________;开口方向是______;最_____值是________.
2.函数y=-2x2+3的图象可由函数_____________的图象向____平移_________个单位得到.
3.把函数y=-3x2的图象向下平移2个单位可得到函数_________________的图象.
问题2:你会用类比法画二次函数y=2(x-1)2的图象吗?它与y=2x2有什么异同吗?它有哪些性质呢?
二、探究交流,获取新知
请你在同一坐标系中画出下列函数的图象:
(1)y=2x2 (2)y=2(x-1)2
完成下表:
x
…
-4
-3
-2
-1
0
1
2
3
4
…
2x2
…
…
2(x-1)2
…
…
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
生:在同一坐标系中画出这两个函数图象,
议一议:(1)二次函数y=2(x-1)2的图象与y=22的图象有什么关系?
生:二次函数y=2(x-1)2的图象是由二次函数y=2x2的图象向右平移1个单位得到的.
(2)二次函数y=2(x-1)2的图象的开口方向、对称轴和顶点坐标分别是什么?
生:开口向上,对称轴为x=1,顶点坐标为(1,0)
(3)二次函数y=2(x-1)2当x取何值时,y的值随x值的增大而增大?当x取何值时,y的值随x值的增大而减小?
生:当x<1时,y的值随x值的增大而增大;当x>1时,y的值随x值的增大而减小.
(4)你能发现二次函数y=2(x-1)2的图象与二次函数y=2x2的图象有什么关系吗?
生:二次函数y=2(x-1)2的图象是由二次函数y=2x2的图象向左平移1个单位得到的.
结论:二次函数y=2x2,y=2(x-1)2,y=2(x+1)2的图象都是抛物线,并且形状相同,只是位置不同. 将函数y=2x2的图象向右平移1个单位长度,就得到函数y=2(x-1)2的图像;将函数y=2x2的图象向左平移1个单位长度,就得到函数y=2(x+1)2的图像.
想一想:由二次函数y=2x2的图象,你能得二次函数y=2x2-,y=2(x+3)2,y=2(x+3)2-的图象吗?
生:由二次函数y=2x2的图象向下平移个单位长度可得二次函数y=2x2-的图象;由二次函数y=2x2的图象向左平移3个单位长度能得二次函数y=2(x+3)2的图象;由二次函数y=2x2的图象先向左平移3个单位长度,再向下平移个单位长度,能得二次函数y=2(x-3)2-的图象.
归纳总结:二次函数y=a(x-h)2+k与二次函数y=ax2的图象有什么关系?
二次函数y=a(x-h)2+k的图象是由二次函数y=ax2的图象先向左(或向右)平移|h|个单位长度,再向上(或向下)平移|k|个单位长度得到的.
h<0时,图象向左平移;h>0时,图象向右平移.
k<0时,图象向下平移;k>0时,图象向上平移.
一般地,平移二次函数y=ax2的图象便可得到二次函数y=a(x-h)2+k的图象.因此,二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标如下表所示:
开口方向
对称轴
顶点坐标
y=a(x-h)2+k
向上(a>0)
直线x=h
(0,0)
向下(a<0)
三、随堂练习
1.回答下列问题:
二次函数y=3(x+2)2的图象与二次函数y=-3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?
2.下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x-2)2+1 B.y=(x+2)2+1 C.y=(x-2)2-3 D.y=(x+2)2-3
3.将抛物线y=2(x-1)2向左平移1个单位后所得到的新抛物线的表达式为___________.
4.将抛物线y=-x2先向上平移2个单位,再向右平移1个单位后,得到的抛物线的表达式为____________.
5.若把函数y=x的图象用 E(x,x)记,函数y=2x+1的图象用 E(x,2x+1)记,…,则E(x,x2-2x+1)可以由 E(x,x2)怎样平移得到( )
A.向上平移1个单位 B.向下平移1个单位
C.向左平移1个单位 D.向右平移1个单位
例2 已知二次函数.
(1)指出它的图象可以看做是函数的图象经过怎样的变换而得到的;
(2)指出图象的开口方向、对称轴和顶点坐标;
(3)求出图象与坐标轴的交点坐标,并画出它的示意图.
六、自我小结,获取感悟
1.y=a(x-h)2+k的图象特征.
2.y=a(x-h)2+k的图象与y=ax2的图象的关系.
第四课时
教学目标
知识与技能
1.会用配方法将y=ax2+bx+c化成y=a(x-h)2+k形式,体会建立二次函数的对称轴和顶点坐标公式的必要性;
2.能够利用二次函数的对称轴和顶点坐标公式解决有关函数问题;
3.掌握系数a、b、c对二次函数图象的影响和作用;
4.通过操作、探究的过程,提高学生对知识的理解和把握能力.
过程与方法
1.通过对二次函数y=ax2+bx+c的图象和性质的探究,培养学生的概括能力,解决实际问题的能力;
2.通过学生的合作交流来解决函数问题,培养学生的合作交流能力.
情感、态度与价值观
1.经历将一些实际问题抽象为数学问题的过程,掌握数学的基础知识和基本技能,并能解决简单的问题;
2.初步认识数学与人类生活的密切联系及对人类历史发展的作用.
教学重点与难点
重点:使学生会运用二次函数的对称轴和顶点坐标公式解决实际问题.
难点:理解并把握数学问题与实际问题相联系的过程.
教学准备:
多媒体课件
教学过程
一、知识回顾,导入新课
问题1:二次函数y=-2(x-3)2+5的开口_______,对称轴是_________,顶点坐标是____.它是由二次函数y=-2x2先向_____平移____个单位长度,再向_____平移____个单位长度得到的.
问题2:对于二次函数y=a(x-h)2+k
(1)当a>0时,它的开口______,对称轴是___________,顶点坐标是__________________.
(2)当a<0时,它的开口________,对称轴是____________,顶点坐标是_________________.
问题3:我们已经认识了形如y=a(x-h)2+k的二次函数的图象和性质,你能研究二次函数y=2x2-4x+5的图象吗?
二、探究交流,获取新知
请你利用已学过的知识将二次函数y=2x2-4x+5化成y=a(x-h)2+k的形式.
解: y=2x2-4x+5
=2(x2-2x)+5
=2(x2-2x+1-1)+5
=2(x-1)2-2+5
=2(x-1)2+3
三、知识讲解
1.求二次函数y=2x2-8x+7图象的对称轴和顶点坐标.
解析:要求二次函数y=2x2-8x+7图象的对称轴和顶点坐标. 只需将它化为y=a(x-h)2+k的形式.
解:y=2x2-8x+7
=2(x2-4x)+7
=2(x2-4x+4)-8+7
=2(x-2)2-1
因此,二次函数y=2x2-8x+7图象的对称轴是直线x=2,顶点坐标为(2,-1).
做一做:
确定下列二次函数图象的对称轴和顶点坐标:
(1)y=3x2-6x+7 (2)y=2x2-12x+8
生:学生解答,教师巡视,发现问题即时解答.
2.求二次函数y=ax2+bx+c图象的对称轴和顶点坐标.
生:指点一名学生上黑板解答,教师点拨.
解:把二次函数y=ax2+bx+c的右边配方,得:
y=ax2+bx+c
=a(x2+x)+c
=a[x2+2·x+()2-()2]+c
=a(x+)2+
因此,二次函数y=ax2+bx+c图象的对称轴是直线 x=-,顶点坐标为(-,).
点拨:由此我们把此称之为求二次函数图象的对称轴和顶点坐标的公式
四、随堂练习
1.用配方法确定下列函数的对称轴和顶点坐标
(1)y=2x2-12x+3; (2)y=-5x2+80x-319;
(3)y=2(x-)(x-2); (4)y=3(2x+1)(2-x).
合作交流:二次函数图象与系数a、b、c之间有何关系?
a决定抛物线的形状、开口方向.
当a>0时,抛物线开口向上,当a<0时,抛物线开口向下,越大抛物线的开口越小.
b影响对称轴的位置.
当ab>0时,抛物线的对称轴在y轴的左侧;当b=0时,抛物线的对称轴是y轴,当ab<0时,抛物线的对称轴在y轴的右侧.
c确定抛物线与y轴的交点位置.
当c>0时,抛物线与y轴的交点在y轴的正半轴上,当c=0时,抛物线经过坐标原点,当c<0时,抛物线与y轴的交点在y轴的负半轴上
例3 已知:抛物线y=-3x2+12x-8.(1)求出它的对称轴和顶点坐标;(2)求出图象与坐标轴的交点坐标,并画出示意图.
例4 已知某抛物线的顶点坐标为(-2,1),且与y轴相交于点(0,4),求这个抛物线所表示的二次函数的表达式.
五、挑战自我:
1.(2014?遵义)已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图,其中正确的是( )
A. B. C. D.
2.若一次函数y=x2-2x+c的图象与y轴的交为(0,-3),则此二次函数有( )
A.最小值-2 B.最小值-3 C.最小值-4 D.最大值-4
六、自我小结,获取感悟
1.对自己说,你在本节课中学习了哪些知识点?有何收获?
2.对同学说,你有哪些学习感悟和温馨提示?
3.对老师说,你还有哪些困惑?
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
