人教版五年级数学下册图形的旋转 147张PPT
文档属性
| 名称 | 人教版五年级数学下册图形的旋转 147张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 21:16:07 | ||
图片预览








文档简介
课件147张PPT。图形的旋转 食碗中的图案你一定不陌生,你还能不能在生活中找到类似的旋转的例子吗?图片欣赏图片欣赏议一议
(1)上面情景中的转动现象,有什么共同的特征?
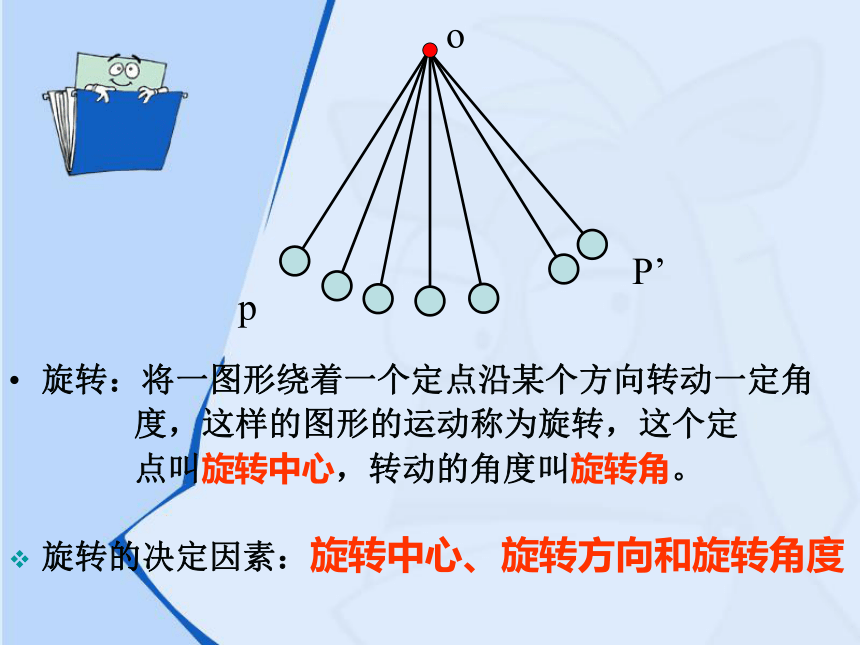
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?pP’o旋转:将一图形绕着一个定点沿某个方向转动一定角
度,这样的图形的运动称为旋转,这个定
点叫旋转中心,转动的角度叫旋转角。旋转的决定因素:旋转中心、旋转方向和旋转角度(4)对应点到旋转中心的距离相等.旋转的基本性质
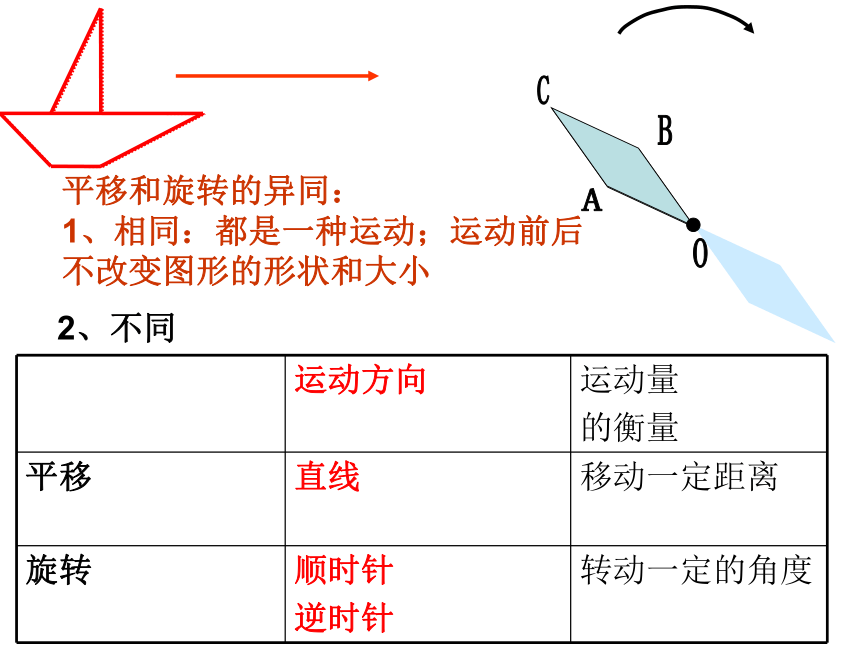
(1)旋转不改变图形的大小和形状.(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
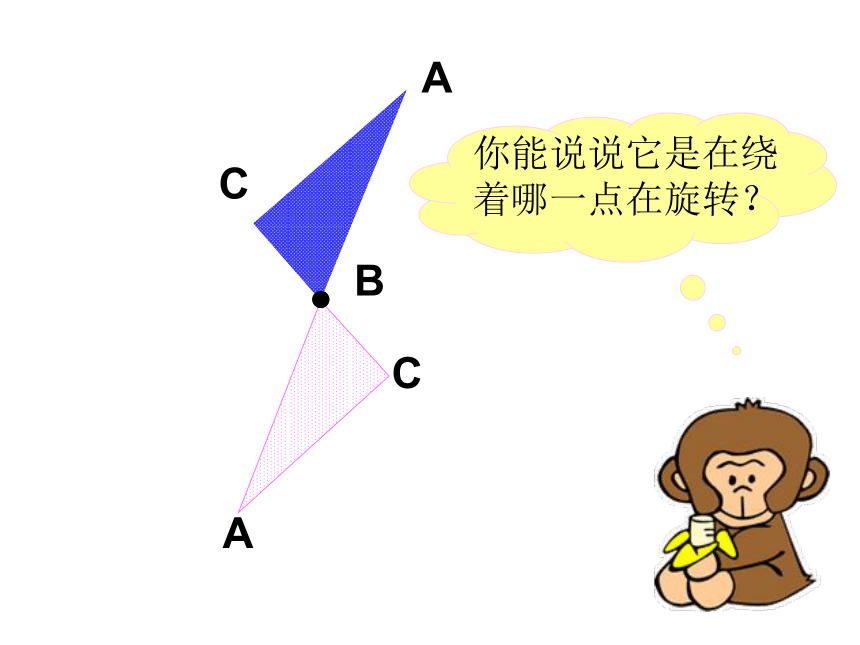
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?图片欣赏BACACABCBCA指针从“12”绕点o顺时针旋转300到“1”121234567891011O指针从“1”绕点O 顺时针旋转600到( )121234567891011O3指针从“3”绕点O 顺时针旋转 ( )到“6”121234567891011O900121234567891011O指针从“6”绕点O 顺时针旋转 ( )到“12”1800旋转的风车风车绕O点逆时针旋转()0。O风车绕O点逆时针旋转()0。O画出三角形AOB 顺时针旋转900后的图形。OA`B` 下面的图案分别是由哪个图形旋转而成的?利用旋转画一朵小花。利用平移或旋转,对称制作出漂亮的图形。O旋转900O旋转1800O旋转3600按上面的方法试一试,你会发现下面的图形有什么特点?与时针旋转方向相同的是顺时针,
与时针旋转方向相反的是逆时针。A你会把右边的三角板绕A点旋转90。吗?A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。从6:00到9:00,时针旋转了( ) 。 。90( )千克的物品可以使指针按顺时针
方向旋转90。 。1指针按顺时针方向旋转90。 ,从A
旋转( );指针按逆时针方向旋转90。 ,从B
旋转( )。DCA如何画三角板顺时针旋转900后的图形?AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗? 通过本节课的学习,同学们要对图形的旋转有一个认识。能够把一个图形顺时针或者逆时针旋转90°,感受旋转在生活中的应用。小 结一、复习导入,揭示课题问题:1.还记得这个三角尺的位置是怎样变化的吗? 旋转时点O的位置不变,并且每旋转一次三角尺的两条直角边都绕点O顺时针旋转了90°。2.三角尺的旋转有什么特点?二、探究新知,明确画法画出三角形AOB绕点O顺时针旋转90°后的图形。问题:1.自己试着画一画。2.你是怎么画的?二、探究新知,明确画法画出三角形AOB绕点O顺时针旋转 90°后的图形。1.绕点 O 旋转,点 O 的位置不变。2.先画 OA′,OA 顺时针旋转 90°后的位置 OA′,OA′垂直于 OA, 点 A′与点 O 的距离应该是 4 格。3.先画 OB′,OB 顺时针旋转 90°后的位置 OB′,OB′垂直于 OB, 点 B′与点 O 的距离应该是 4 格。4.连接 A′B′,三角形 A′O B′就是AOB 绕点O顺时针旋转 90°后的图形。A′B′ 二、探究新知,明确画法画出三角形AOB 绕点O逆时针旋转 90°后的图形。问题:1.自己试着画一画。2.你是怎么画的?二、探究新知,明确画法画出三角形AOB绕点O逆时针旋转 90°后的图形。1.绕点 O 旋转,点 O 的位置不变。2.先画 OA′,OA 逆时针旋转 90°后的位置 OA′,OA′垂直于 OA, 点 A′与点 O 的距离应该是 4 格。 3.先画 OB′,OB 逆时针旋转 90°后的位置 OB′,OB′垂直于 OB, 点 B′与点 O 的距离应该是 4 格。 4.连接 A′B′,三角形 A′O B′就是 AOB 绕点 O 逆时针旋转 90°后的图形。A′B′三、巩固提升问题:你是怎样想的?画出三角形AOB绕点O逆时针旋转 90°后的图形。
三、巩固提升问题:绕点 O 旋转长方形。你有什么发现吗?如图,长方形的两条对称轴相交于点O。三、巩固提升问题:按上面的方法试一试,你发现下面的图形有什么特点?如图,长方形的两条对称轴相交于点 O。四、拓展应用一、复习导入,揭示课题问题:1.知道七巧板吗?2.你对七巧板有什么了解?二、探究新知,明确画法七巧板经过平移或旋转后得到了鱼图。问题:通过读题你知道了哪些信息? 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:1.你能自己试着完成吗? 鱼图只有一个外形的轮廓,要先把鱼图分割出七巧板中的七块,再判断每块板平移或旋转后的位置,然后看每块板是如何运动的。七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。2.说说你打算怎么做。二、探究新知,明确画法问题:怎样判断每块板的位置?七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。1235476我直接在鱼图上把鱼图分为……二、探究新知,明确画法七巧板经过平移或旋转后得到了鱼图。问题:怎样判断每块板的位置? 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。1234567我可以用七巧板拼拼看。二、探究新知,明确画法问题:这时板1是怎样平移或旋转的?板1先向下平移1格,再向右平移9格。七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:这时其他板分别是怎样平移或旋转的? 七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:1.还有其他答案吗?七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。23417562.这时每块板是怎样平移或旋转的?三、巩固提升问题:你是怎样想的?左图是被打乱的4张图片,怎样才能还原成右图?四、拓展应用七巧板除“七巧板”的名称外,还有不少名称:“益智图”、“智慧板”、“唐图”等都是七巧板的别称。是汉族民间流传的智力玩具。它是由唐代的宴几演变而来的,原为文人的一种室内游戏,后在民间演变为拼图板玩具。现七巧板系由一块正方形切割为五个小勾股形,将其拼凑成各种事物图形,如人物、动植物、房亭楼阁、车轿船桥等,可一人玩,也可多人进行比赛。利用七巧板可以阐明若干重要几何关系,其原理便是古算术中的“出入相补原理”。四、拓展应用七巧板拼图AOB45°点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;∠A的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题一CBAO如图,将△ ABC绕着外面的点O旋转60°将整个△ ABC旋转到△A’B’C’的位置。点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;∠C的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题二DEFCBAO如图, △ DEF是由△ ABC绕点O旋转得到的,你能说出其中的对应点、对应角和对应线段吗?问题三1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A。
(2)旋转了60°。
(3)点M转到了AC 的中点位置上。 2、如图,△ABC和 △ ADE都是等腰直角三角形, ∠ C和∠ AED都是直角,点E在AB上,如果△ABC经旋转后能与△ ADE重合,那么哪一点是旋转中心?旋转了多少度?ACBDE试一试 图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的? 简单的旋转作图AO点的旋转作法例1 将A点绕O点沿顺时针方向旋转60?.分析:作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.B 简单的旋转作图AO线段的旋转作法例2 将线段AB绕O点沿顺时针方向旋转60?.分析:作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD简单的旋转作图图形的旋转作法例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.分析:作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE 简单的旋转作图练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.探索发现 联系前面所学内容,我们应如何探索出旋转所具有的特征? 课堂回顾:这节课,主要学习了什么?在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转旋转的概念:旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等
(1)上面情景中的转动现象,有什么共同的特征?
(2)钟表的指针、秋千在转动过程中,其形状、大小、位置是否发生变化呢?pP’o旋转:将一图形绕着一个定点沿某个方向转动一定角
度,这样的图形的运动称为旋转,这个定
点叫旋转中心,转动的角度叫旋转角。旋转的决定因素:旋转中心、旋转方向和旋转角度(4)对应点到旋转中心的距离相等.旋转的基本性质
(1)旋转不改变图形的大小和形状.(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.平移和旋转的异同:
1、相同:都是一种运动;运动前后 不改变图形的形状和大小BACO2、不同
可以看作是一个花瓣连续4次旋转所形成的,每次旋转分别等于720 , 1440 , 2160 , 2880
思考题:香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的?图片欣赏BACACABCBCA指针从“12”绕点o顺时针旋转300到“1”121234567891011O指针从“1”绕点O 顺时针旋转600到( )121234567891011O3指针从“3”绕点O 顺时针旋转 ( )到“6”121234567891011O900121234567891011O指针从“6”绕点O 顺时针旋转 ( )到“12”1800旋转的风车风车绕O点逆时针旋转()0。O风车绕O点逆时针旋转()0。O画出三角形AOB 顺时针旋转900后的图形。OA`B` 下面的图案分别是由哪个图形旋转而成的?利用旋转画一朵小花。利用平移或旋转,对称制作出漂亮的图形。O旋转900O旋转1800O旋转3600按上面的方法试一试,你会发现下面的图形有什么特点?与时针旋转方向相同的是顺时针,
与时针旋转方向相反的是逆时针。A你会把右边的三角板绕A点旋转90。吗?A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点顺时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。A把三角板绕A点逆时针旋转90。从6:00到9:00,时针旋转了( ) 。 。90( )千克的物品可以使指针按顺时针
方向旋转90。 。1指针按顺时针方向旋转90。 ,从A
旋转( );指针按逆时针方向旋转90。 ,从B
旋转( )。DCA如何画三角板顺时针旋转900后的图形?AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。AB把长方形绕A点顺时针旋转90。把小旗图绕B点逆时针旋转90。观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗?观察下面三组图形,它们有什么共同的特点?
你能旋转每组中的一个图形,使每组图形都变
成一个长方形吗? 通过本节课的学习,同学们要对图形的旋转有一个认识。能够把一个图形顺时针或者逆时针旋转90°,感受旋转在生活中的应用。小 结一、复习导入,揭示课题问题:1.还记得这个三角尺的位置是怎样变化的吗? 旋转时点O的位置不变,并且每旋转一次三角尺的两条直角边都绕点O顺时针旋转了90°。2.三角尺的旋转有什么特点?二、探究新知,明确画法画出三角形AOB绕点O顺时针旋转90°后的图形。问题:1.自己试着画一画。2.你是怎么画的?二、探究新知,明确画法画出三角形AOB绕点O顺时针旋转 90°后的图形。1.绕点 O 旋转,点 O 的位置不变。2.先画 OA′,OA 顺时针旋转 90°后的位置 OA′,OA′垂直于 OA, 点 A′与点 O 的距离应该是 4 格。3.先画 OB′,OB 顺时针旋转 90°后的位置 OB′,OB′垂直于 OB, 点 B′与点 O 的距离应该是 4 格。4.连接 A′B′,三角形 A′O B′就是AOB 绕点O顺时针旋转 90°后的图形。A′B′ 二、探究新知,明确画法画出三角形AOB 绕点O逆时针旋转 90°后的图形。问题:1.自己试着画一画。2.你是怎么画的?二、探究新知,明确画法画出三角形AOB绕点O逆时针旋转 90°后的图形。1.绕点 O 旋转,点 O 的位置不变。2.先画 OA′,OA 逆时针旋转 90°后的位置 OA′,OA′垂直于 OA, 点 A′与点 O 的距离应该是 4 格。 3.先画 OB′,OB 逆时针旋转 90°后的位置 OB′,OB′垂直于 OB, 点 B′与点 O 的距离应该是 4 格。 4.连接 A′B′,三角形 A′O B′就是 AOB 绕点 O 逆时针旋转 90°后的图形。A′B′三、巩固提升问题:你是怎样想的?画出三角形AOB绕点O逆时针旋转 90°后的图形。
三、巩固提升问题:绕点 O 旋转长方形。你有什么发现吗?如图,长方形的两条对称轴相交于点O。三、巩固提升问题:按上面的方法试一试,你发现下面的图形有什么特点?如图,长方形的两条对称轴相交于点 O。四、拓展应用一、复习导入,揭示课题问题:1.知道七巧板吗?2.你对七巧板有什么了解?二、探究新知,明确画法七巧板经过平移或旋转后得到了鱼图。问题:通过读题你知道了哪些信息? 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:1.你能自己试着完成吗? 鱼图只有一个外形的轮廓,要先把鱼图分割出七巧板中的七块,再判断每块板平移或旋转后的位置,然后看每块板是如何运动的。七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。2.说说你打算怎么做。二、探究新知,明确画法问题:怎样判断每块板的位置?七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。1235476我直接在鱼图上把鱼图分为……二、探究新知,明确画法七巧板经过平移或旋转后得到了鱼图。问题:怎样判断每块板的位置? 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。1234567我可以用七巧板拼拼看。二、探究新知,明确画法问题:这时板1是怎样平移或旋转的?板1先向下平移1格,再向右平移9格。七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:这时其他板分别是怎样平移或旋转的? 七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。二、探究新知,明确画法问题:1.还有其他答案吗?七巧板经过平移或旋转后得到了鱼图。 请在鱼图中画出相应的每块板的轮廓线,标出序号同时说明每块板是怎样平移或旋转的。23417562.这时每块板是怎样平移或旋转的?三、巩固提升问题:你是怎样想的?左图是被打乱的4张图片,怎样才能还原成右图?四、拓展应用七巧板除“七巧板”的名称外,还有不少名称:“益智图”、“智慧板”、“唐图”等都是七巧板的别称。是汉族民间流传的智力玩具。它是由唐代的宴几演变而来的,原为文人的一种室内游戏,后在民间演变为拼图板玩具。现七巧板系由一块正方形切割为五个小勾股形,将其拼凑成各种事物图形,如人物、动植物、房亭楼阁、车轿船桥等,可一人玩,也可多人进行比赛。利用七巧板可以阐明若干重要几何关系,其原理便是古算术中的“出入相补原理”。四、拓展应用七巧板拼图AOB45°点B的对应点是___;线段OB的对应线段是线段___;线段AB的对应线段是线段___;∠A的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题一CBAO如图,将△ ABC绕着外面的点O旋转60°将整个△ ABC旋转到△A’B’C’的位置。点B的对应点是___;线段BC的对应线段是线段___;线段AB的对应线段是线段___;∠C的对应角是___;∠B的对应角是___;旋转中心是点___;旋转的角度是___。
问题二DEFCBAO如图, △ DEF是由△ ABC绕点O旋转得到的,你能说出其中的对应点、对应角和对应线段吗?问题三1、如图,△ABC是等边三角形,D是BC上一点,△ABD经过旋转后到达△ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3) 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
解:(1)旋转中心是A。
(2)旋转了60°。
(3)点M转到了AC 的中点位置上。 2、如图,△ABC和 △ ADE都是等腰直角三角形, ∠ C和∠ AED都是直角,点E在AB上,如果△ABC经旋转后能与△ ADE重合,那么哪一点是旋转中心?旋转了多少度?ACBDE试一试 图中是否存在这样的两个三角形,其中一个是通过另一个旋转得到的? 简单的旋转作图AO点的旋转作法例1 将A点绕O点沿顺时针方向旋转60?.分析:作法:
1. 以点O为圆心,OA长为半径画圆;
2. 连接OA, 用量角器或三角板(限
特殊角)作出∠AOB,与圆周交
于B点;
3. B点即为所求作.B 简单的旋转作图AO线段的旋转作法例2 将线段AB绕O点沿顺时针方向旋转60?.分析:作法:
将点A绕点O顺时针旋转60?,得
点C;
2. 将点B绕点O顺时针旋转60 ?,得点D ;
3. 连接CD, 则线段CD即为所求作.CBD简单的旋转作图图形的旋转作法例3 如图,△ABC绕C点旋转后,顶点A得对应点为点D. 试确定顶点B对应点的位置以及旋转后的三角形.分析:作法一:
1. 连接CD;
2. 以CB为一边,作∠BCE,使得∠BCE=∠ACD ;
3. 在射线CB上截取CE,使得CE=CB;
4. 连接DE,则△DEC即为所求作.CABDE 简单的旋转作图练习1
将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90?,作出旋转后的图案.探索发现 联系前面所学内容,我们应如何探索出旋转所具有的特征? 课堂回顾:这节课,主要学习了什么?在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转旋转的概念:旋转的性质:1、旋转不改变图形的大小和形状.2、任意一对对应点与旋转中心的连线所成的
角度都是旋转角,旋转角相等.3、对应点到旋转中心的距离相等
