5.4扇形 教案
图片预览
文档简介
扇形
教学内容:教材75页内容
教学目标:
理解和建立扇形的概念,认识圆心角和弧。
在认识圆心角和弧的过程中,培养学生的观察能力。
教学重点:
建立扇形的概念。
教学难点:
理解圆心角的大小与扇形大小的关系。
教学准备:
师:课件,圆规,三角板,四个扇形
生:量角器,圆规,三角板
教学过程:
复习旧知
你能指出这个圆的圆心、半径和直径吗?
认识扇形
出示:扇贝、扇形藻、搁物架、孔雀开屏、少数民族的饰品。
问:这些物体的外形有什么相同的地方?
你觉得什么是扇形?它有什么特点?
扇形到底是什么样的,有哪些知识和它有关,看书75页思考以下问题
什么是弧?应怎样读写?
什么是圆心角?
什么是扇形?
扇形与三角形有什么不同?
3.反馈新知
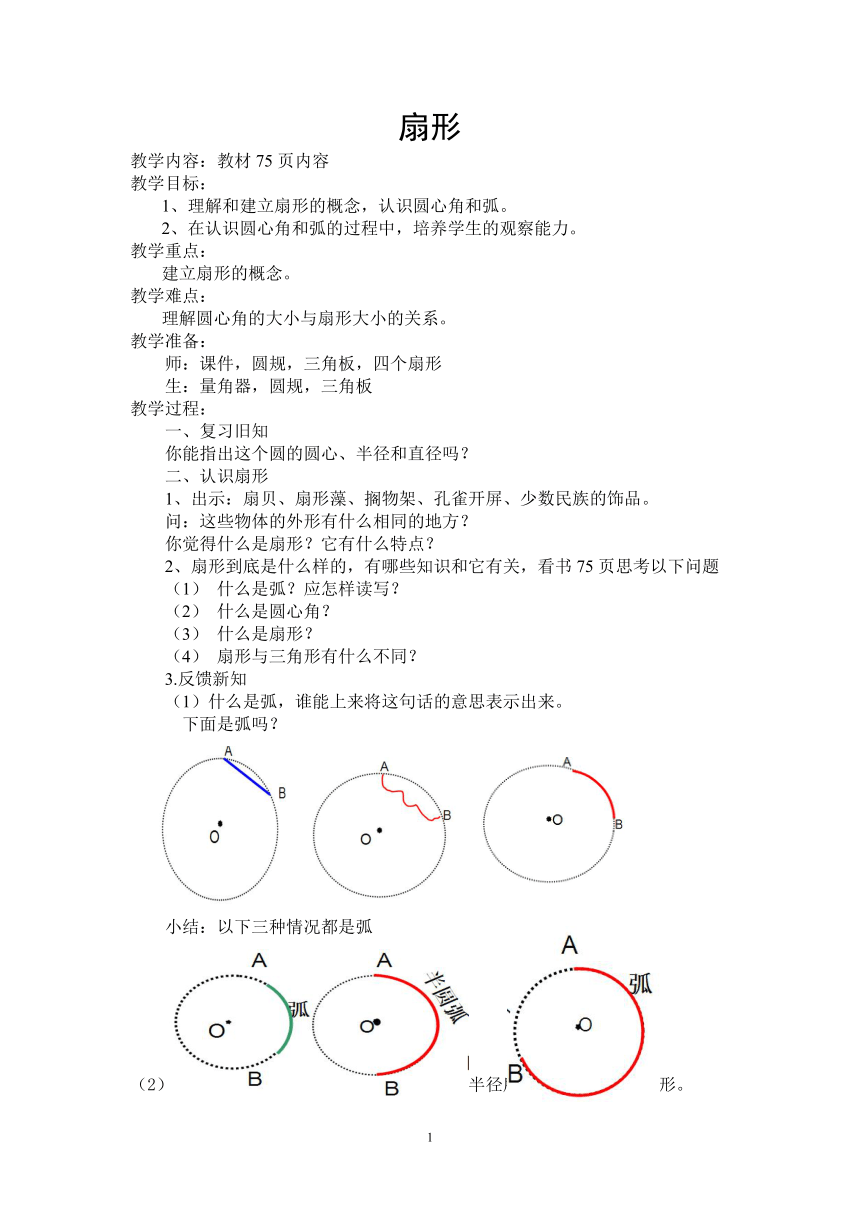
(1)什么是弧,谁能上来将这句话的意思表示出来。
下面是弧吗?
小结:以下三种情况都是弧
(2)扇形 一条弧和经过这条弧两端的两条半径所围城的图形叫做扇形。
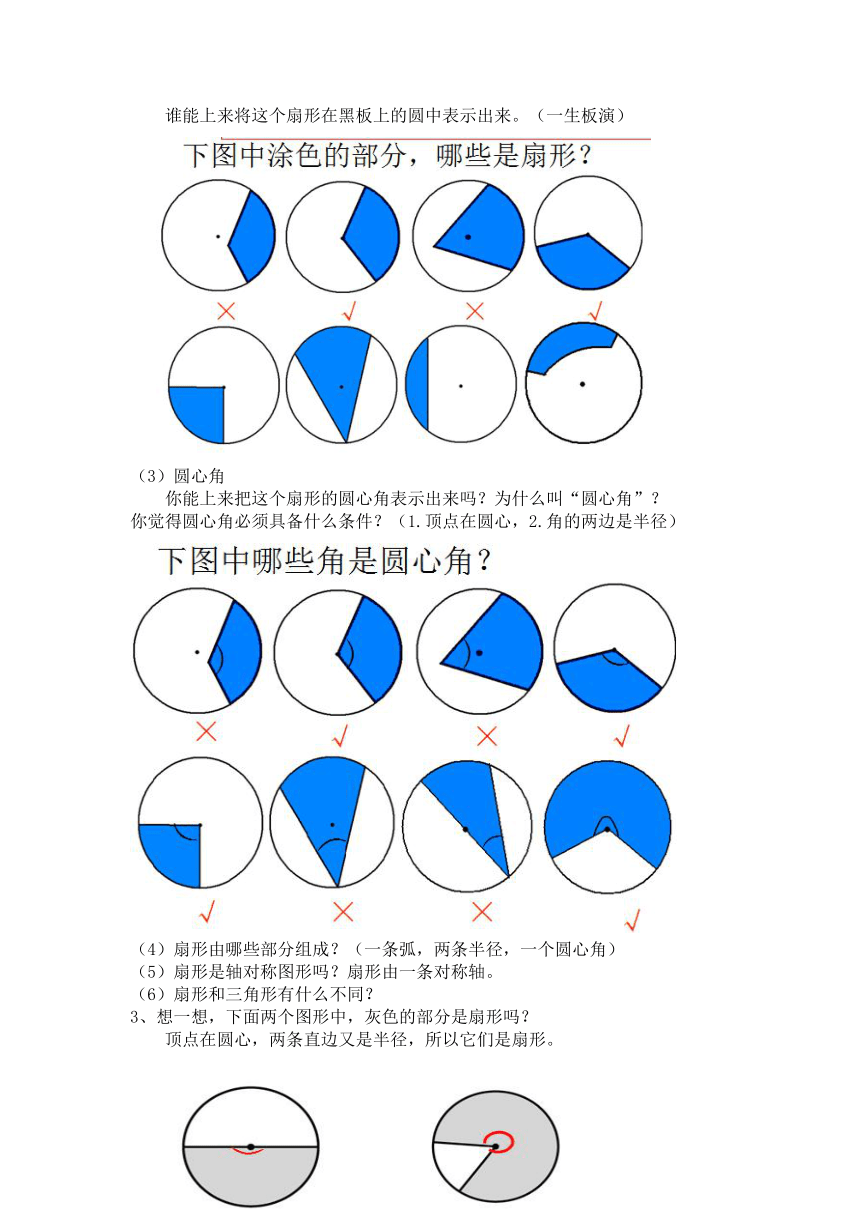
谁能上来将这个扇形在黑板上的圆中表示出来。(一生板演)
(3)圆心角
你能上来把这个扇形的圆心角表示出来吗?为什么叫“圆心角”?
你觉得圆心角必须具备什么条件?(1.顶点在圆心,2.角的两边是半径)
(4)扇形由哪些部分组成?(一条弧,两条半径,一个圆心角)
(5)扇形是轴对称图形吗?扇形由一条对称轴。
(6)扇形和三角形有什么不同?
3、想一想,下面两个图形中,灰色的部分是扇形吗?
顶点在圆心,两条直边又是半径,所以它们是扇形。
4、画一个半径是2厘米的圆,然后在圆中画一个圆心角是100°的扇形。
学生自主画,反馈方法,并讲一讲在画的时候有什么要提醒大家的。
探索发现,应用新知
1、思考:扇形的大小与什么有关呢?
准备4个扇形:
半径10厘米,圆心角45°;②半径14厘米,圆心角45°;
半径14厘米,圆心角85°;④半径12厘米,圆心角60°.
(1)①和②比,哪个扇形面积大?(圆心角相等,半径不同,扇形的大小不同)。多出的是哪部分?扇形的大小可能跟谁有关?
(2)②和③比:圆心角不相等,半径相等,扇形的大小不同。扇形大小可能跟谁有关?
(3)③和④比 比不出大小,那怎么办?(算一算)
你觉得扇形算面积需要知道哪些数据?
小组合作探究:扇形的大小与哪些因素有关。
小结:扇形的大小是由扇形的圆心角和半径所决定的。
3.以半圆为弧的扇形的圆心角是多少度?以四分之一圆为弧的扇形呢?
下面圆中的扇形面积各是圆面积的几分之几?并说明理由。
已知扇形的圆心角为120°,半径为3厘米,求这个扇形的周长和面积。
生活中的扇形
像这样一个圆环被截得的部分叫做扇环。
全课总结
这节课你有哪些收获?
《扇形的认识》教学反思
《扇形的认识》这部分内容是圆的相关知识的延伸与扩展,本节课尊重教材的设计,把握好了教学的重点与难点,让学生经历了由物到形再到概念的这样一个认识图形的过程,符合认知的规律,用“联系”的观点来教学,抓住扇形与圆形的联系,扇环与扇形、圆环的联系,同时注重发展学生的空间观念。
课堂上我直接出示图片引出“扇形”,先让学生说说对于扇形你已经有了哪些认识,了解学生的学习起点。而后让学生自学“弧”、“圆心角”、“扇形”的概念,语言比较抽象,先让学生用自己的理解在板书上体现出来,再利用课件的演示学生容易理解并可见其形象,对于各个概念逐个击破。认识扇形后,而后动手画一画,先画一个指定大小的圆,再在里面画扇形,进一步体会扇形是圆的一部分。
扇形大小与谁有关是本节课的重点也是难点,我通过4个扇形的两两对比,形象地解决了半径和圆心角这两个因素对扇形大小的决定作用。而后利用圆与扇形的关系,探索扇形面积计算及周长计算的方法和注意点。最后是扇环和圆环的关系。
没能及时捕捉有价值的课堂生成很遗憾。记得一位专家说过:“数学课堂因生成而精彩”。所谓数学课堂生成就是指在教师与学生、学生与学生合作、对话、碰撞的数学课堂中,现时生成的超出教师预设方案之外的新问题、新情况。它随着教学环境、学习主体、学习方式的变化而变化,根据教师的不同处理而呈现出不同的价值,使数学课堂呈现出变化、生机勃勃的特点。本节课学生在回答“哪些物体的外形是扇形的?”这一问题时,一名学生指着教室黑板上方的圆形钟表说:“时针、分针及它们之间的弧所围成的部分是扇形。”这是出乎教师的预料的,还好我反应过来,他的答案不够准确。若当时能让同学们一起交流,请大家来判断这位同学回答的是否正确,并说明理由,我想学生们就会在交流中发现时针与分针长短不一,即便在它们之间画一条弧线,所围成的部分也不是扇形。“那怎样才能形成扇形?”教师的追问会再一次引发学生的思考。我想这样课堂效果会更好。
教学内容:教材75页内容
教学目标:
理解和建立扇形的概念,认识圆心角和弧。
在认识圆心角和弧的过程中,培养学生的观察能力。
教学重点:
建立扇形的概念。
教学难点:
理解圆心角的大小与扇形大小的关系。
教学准备:
师:课件,圆规,三角板,四个扇形
生:量角器,圆规,三角板
教学过程:
复习旧知
你能指出这个圆的圆心、半径和直径吗?
认识扇形
出示:扇贝、扇形藻、搁物架、孔雀开屏、少数民族的饰品。
问:这些物体的外形有什么相同的地方?
你觉得什么是扇形?它有什么特点?
扇形到底是什么样的,有哪些知识和它有关,看书75页思考以下问题
什么是弧?应怎样读写?
什么是圆心角?
什么是扇形?
扇形与三角形有什么不同?
3.反馈新知
(1)什么是弧,谁能上来将这句话的意思表示出来。
下面是弧吗?
小结:以下三种情况都是弧
(2)扇形 一条弧和经过这条弧两端的两条半径所围城的图形叫做扇形。
谁能上来将这个扇形在黑板上的圆中表示出来。(一生板演)
(3)圆心角
你能上来把这个扇形的圆心角表示出来吗?为什么叫“圆心角”?
你觉得圆心角必须具备什么条件?(1.顶点在圆心,2.角的两边是半径)
(4)扇形由哪些部分组成?(一条弧,两条半径,一个圆心角)
(5)扇形是轴对称图形吗?扇形由一条对称轴。
(6)扇形和三角形有什么不同?
3、想一想,下面两个图形中,灰色的部分是扇形吗?
顶点在圆心,两条直边又是半径,所以它们是扇形。
4、画一个半径是2厘米的圆,然后在圆中画一个圆心角是100°的扇形。
学生自主画,反馈方法,并讲一讲在画的时候有什么要提醒大家的。
探索发现,应用新知
1、思考:扇形的大小与什么有关呢?
准备4个扇形:
半径10厘米,圆心角45°;②半径14厘米,圆心角45°;
半径14厘米,圆心角85°;④半径12厘米,圆心角60°.
(1)①和②比,哪个扇形面积大?(圆心角相等,半径不同,扇形的大小不同)。多出的是哪部分?扇形的大小可能跟谁有关?
(2)②和③比:圆心角不相等,半径相等,扇形的大小不同。扇形大小可能跟谁有关?
(3)③和④比 比不出大小,那怎么办?(算一算)
你觉得扇形算面积需要知道哪些数据?
小组合作探究:扇形的大小与哪些因素有关。
小结:扇形的大小是由扇形的圆心角和半径所决定的。
3.以半圆为弧的扇形的圆心角是多少度?以四分之一圆为弧的扇形呢?
下面圆中的扇形面积各是圆面积的几分之几?并说明理由。
已知扇形的圆心角为120°,半径为3厘米,求这个扇形的周长和面积。
生活中的扇形
像这样一个圆环被截得的部分叫做扇环。
全课总结
这节课你有哪些收获?
《扇形的认识》教学反思
《扇形的认识》这部分内容是圆的相关知识的延伸与扩展,本节课尊重教材的设计,把握好了教学的重点与难点,让学生经历了由物到形再到概念的这样一个认识图形的过程,符合认知的规律,用“联系”的观点来教学,抓住扇形与圆形的联系,扇环与扇形、圆环的联系,同时注重发展学生的空间观念。
课堂上我直接出示图片引出“扇形”,先让学生说说对于扇形你已经有了哪些认识,了解学生的学习起点。而后让学生自学“弧”、“圆心角”、“扇形”的概念,语言比较抽象,先让学生用自己的理解在板书上体现出来,再利用课件的演示学生容易理解并可见其形象,对于各个概念逐个击破。认识扇形后,而后动手画一画,先画一个指定大小的圆,再在里面画扇形,进一步体会扇形是圆的一部分。
扇形大小与谁有关是本节课的重点也是难点,我通过4个扇形的两两对比,形象地解决了半径和圆心角这两个因素对扇形大小的决定作用。而后利用圆与扇形的关系,探索扇形面积计算及周长计算的方法和注意点。最后是扇环和圆环的关系。
没能及时捕捉有价值的课堂生成很遗憾。记得一位专家说过:“数学课堂因生成而精彩”。所谓数学课堂生成就是指在教师与学生、学生与学生合作、对话、碰撞的数学课堂中,现时生成的超出教师预设方案之外的新问题、新情况。它随着教学环境、学习主体、学习方式的变化而变化,根据教师的不同处理而呈现出不同的价值,使数学课堂呈现出变化、生机勃勃的特点。本节课学生在回答“哪些物体的外形是扇形的?”这一问题时,一名学生指着教室黑板上方的圆形钟表说:“时针、分针及它们之间的弧所围成的部分是扇形。”这是出乎教师的预料的,还好我反应过来,他的答案不够准确。若当时能让同学们一起交流,请大家来判断这位同学回答的是否正确,并说明理由,我想学生们就会在交流中发现时针与分针长短不一,即便在它们之间画一条弧线,所围成的部分也不是扇形。“那怎样才能形成扇形?”教师的追问会再一次引发学生的思考。我想这样课堂效果会更好。
