19.6 反比例函数的图象、性质和应用 教案 (2)
文档属性
| 名称 | 19.6 反比例函数的图象、性质和应用 教案 (2) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览


文档简介
《反比例函数的图象、性质和应用》教案
教学目标
知识与技能:
1.会用描点法画反比例函数的图象;
2.结合图象分析并掌握其性质;
3.能灵活运用反比例函数的图象和性质求函数的解析式,进而解决一些较综合的实际问题.
过程与方法:
1.经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想方法,让学生初步认识具体的反比例函数图象的特征;
2.经历观察、分析、交流的过程,逐步提高从函数图象中感受其规律的能力;
3.从较综合的题目的解答中学会使用数形结合的方法.
情感、态度与价值观:
1.由图象的画法和分析,体验数学活动中的探索和创造性,感受数学美,并通过图象的直观教学激发学习兴趣;
2.深刻领会函数解析式与和函数图象之间的联系,体会数形结合及转化的思想方法;
3.通过解决综合题,增强学生的自信心,涵育学生学习数学的兴趣.
教学重点
正确地进行描点、画出图象,理解并掌握反比例的图象和性质,能灵活运用反比例函数的性质解决一些综合问题.
教学难点
1.图象的对称性选点,归纳反比例函数的性质.
2.利用数形结合思想比较大小以及对反比例函数几何意义的理解学会利用图象分析、解决问题.
教学流程
一、情境引入
问题:我们知道一次函数y=kx+b(k≠0)的图象是一条直线、二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,反比例函数的图象是什么样呢?
我们用什么方法画反比例函数的图象呢?
有哪些步骤?
根据k的取值,应该如何分类讨论呢?
引出课题:今天,我们就来研究反比例函数的图象和性质.
二、探究归纳
画出反比例函数和的图象.
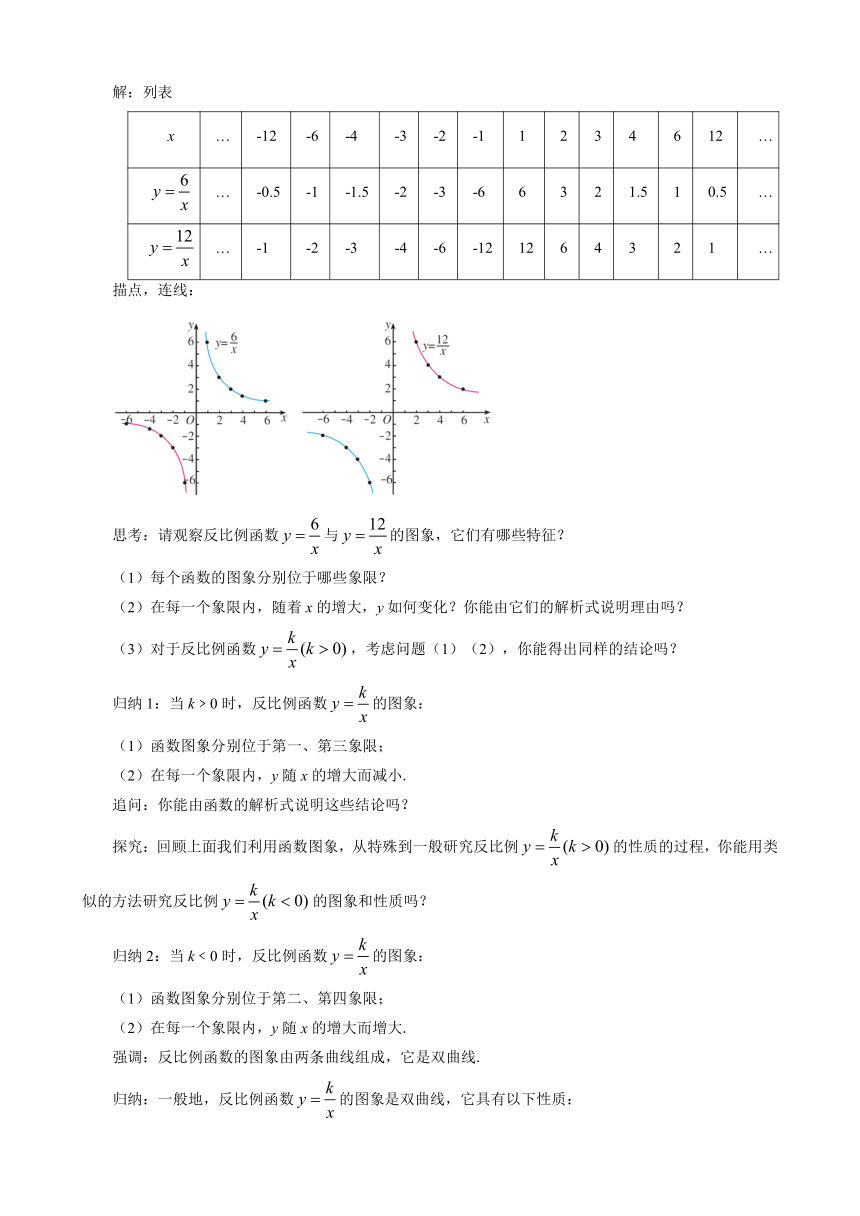
解:列表
x
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
…
…
-0.5
-1
-1.5
-2
-3
-6
6
3
2
1.5
1
0.5
…
…
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
…
描点,连线:
思考:请观察反比例函数与的图象,它们有哪些特征?
(1)每个函数的图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数,考虑问题(1)(2),你能得出同样的结论吗?
归纳1:当k﹥0时,反比例函数的图象:
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随x的增大而减小.
追问:你能由函数的解析式说明这些结论吗?
探究:回顾上面我们利用函数图象,从特殊到一般研究反比例的性质的过程,你能用类似的方法研究反比例的图象和性质吗?
归纳2:当k﹤0时,反比例函数的图象:
(1)函数图象分别位于第二、第四象限;
(2)在每一个象限内,y随x的增大而增大.
强调:反比例函数的图象由两条曲线组成,它是双曲线.
归纳:一般地,反比例函数的图象是双曲线,它具有以下性质:
(1)当k﹥0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k﹤0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
三、解决问题
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题中的作用.今天,我们进一步探讨如何利用反比例函数解决实际问题.
实例1 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸载完毕,那么平均每天至少要卸载多少吨?
解:设轮船上的货物总量为k吨,根据已知条件得
k=30×8=240,
所以v关于t的函数解析式为
.
(2)把t=5代入,得
(吨).
∴如果全部货物恰好用5天卸载完,那么平均每天卸载48吨.
∵对于函数,当t>0时,t越小,v越大.
∴若货物不超过5天卸载完,则平均每天至少要卸载48吨.
实例2 公元前3世纪,有一位科学家说了这样一句名言:“给我一个支点,我可以撬动地球!”你们知道这位科学家是谁吗?这里蕴含什么样的原理呢?
杠杆原理:阻力×阻力臂=动力×动力臂
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5 m.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为1.5 m时,撬动石头至少需要多大的力?
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:(1)根据“杠杆原理”,得
Fl=1200×0.5,
所以F关于l的函数解析式为
.
当l=1.5 m时,
(N).
对于函数,当l=1.5 m 时,F=400N,此时杠杆平衡.
因此,撬动石头至少需要400N的力.
(2)当时,
由得
(m),
3-1.5=1.5(m).
对于函数,当l>0时,l越大,F越小.
因此,若想用力不超过400N的一半,则动力臂至少要加长1.5m.
追问:在我们使用撬棍时,为什么动力臂越长越省力?
例题解析
例1 已知反比例函数的图象经过点p(-6,-2).
(1)求出它的表达式;
(2)画出它在第一象限内的图象;
(3)当自变量x从3增大到9时,函数值y是怎样变化的?
例2 如图,它是反比例函数图象的一支,根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点 A(x1,y1)和点B(x2,y2),如果x1>x2,那么y1和y2有怎样的关系?
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.
∵这个函数的图象的一支位于第一象限,
∴另一支必位于第三象限.
∵这个函数的图象位于第一、第三象限,
∴m-5﹥0,
解得m﹥5.
(2)∵m-5﹥0,
∴在这个函数图象的任一支上,y随x的增大而减小,
∴当x1>x2时,y1﹤y2 .
三、应用提高
1.下列图象中是反比例函数图象的是( )
2.已知反比例函数的图象过点(2,1),则它的图象在________象限,k___0.
3.如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗.
(1)漏斗口的面积S(单位:dm2)与漏斗的深度d有怎样的函数关系?
(2)如果漏斗口的面积为100cm2,则漏斗的深为多少?
答案:(1)(2)30 cm
四、体验收获
说一说你的收获.
1.反比例函数的图象是怎样得到的?画图时要注意什么问题?
2.反比例函数的性质是怎样的?为什么要强调在每一个象限内的性质?
3.在反比例函数图象及性质的应用中体现了数形结合思想,能否谈谈你的体会?
教学目标
知识与技能:
1.会用描点法画反比例函数的图象;
2.结合图象分析并掌握其性质;
3.能灵活运用反比例函数的图象和性质求函数的解析式,进而解决一些较综合的实际问题.
过程与方法:
1.经历画图、观察、猜想、思考等数学活动,向学生渗透数形结合的思想方法,让学生初步认识具体的反比例函数图象的特征;
2.经历观察、分析、交流的过程,逐步提高从函数图象中感受其规律的能力;
3.从较综合的题目的解答中学会使用数形结合的方法.
情感、态度与价值观:
1.由图象的画法和分析,体验数学活动中的探索和创造性,感受数学美,并通过图象的直观教学激发学习兴趣;
2.深刻领会函数解析式与和函数图象之间的联系,体会数形结合及转化的思想方法;
3.通过解决综合题,增强学生的自信心,涵育学生学习数学的兴趣.
教学重点
正确地进行描点、画出图象,理解并掌握反比例的图象和性质,能灵活运用反比例函数的性质解决一些综合问题.
教学难点
1.图象的对称性选点,归纳反比例函数的性质.
2.利用数形结合思想比较大小以及对反比例函数几何意义的理解学会利用图象分析、解决问题.
教学流程
一、情境引入
问题:我们知道一次函数y=kx+b(k≠0)的图象是一条直线、二次函数y=ax2+bx+c(a≠0)的图象是一条抛物线,反比例函数的图象是什么样呢?
我们用什么方法画反比例函数的图象呢?
有哪些步骤?
根据k的取值,应该如何分类讨论呢?
引出课题:今天,我们就来研究反比例函数的图象和性质.
二、探究归纳
画出反比例函数和的图象.
解:列表
x
…
-12
-6
-4
-3
-2
-1
1
2
3
4
6
12
…
…
-0.5
-1
-1.5
-2
-3
-6
6
3
2
1.5
1
0.5
…
…
-1
-2
-3
-4
-6
-12
12
6
4
3
2
1
…
描点,连线:
思考:请观察反比例函数与的图象,它们有哪些特征?
(1)每个函数的图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数,考虑问题(1)(2),你能得出同样的结论吗?
归纳1:当k﹥0时,反比例函数的图象:
(1)函数图象分别位于第一、第三象限;
(2)在每一个象限内,y随x的增大而减小.
追问:你能由函数的解析式说明这些结论吗?
探究:回顾上面我们利用函数图象,从特殊到一般研究反比例的性质的过程,你能用类似的方法研究反比例的图象和性质吗?
归纳2:当k﹤0时,反比例函数的图象:
(1)函数图象分别位于第二、第四象限;
(2)在每一个象限内,y随x的增大而增大.
强调:反比例函数的图象由两条曲线组成,它是双曲线.
归纳:一般地,反比例函数的图象是双曲线,它具有以下性质:
(1)当k﹥0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k﹤0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
三、解决问题
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题中的作用.今天,我们进一步探讨如何利用反比例函数解决实际问题.
实例1 码头工人每天往一艘轮船上装载30吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货天数t之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸载完毕,那么平均每天至少要卸载多少吨?
解:设轮船上的货物总量为k吨,根据已知条件得
k=30×8=240,
所以v关于t的函数解析式为
.
(2)把t=5代入,得
(吨).
∴如果全部货物恰好用5天卸载完,那么平均每天卸载48吨.
∵对于函数,当t>0时,t越小,v越大.
∴若货物不超过5天卸载完,则平均每天至少要卸载48吨.
实例2 公元前3世纪,有一位科学家说了这样一句名言:“给我一个支点,我可以撬动地球!”你们知道这位科学家是谁吗?这里蕴含什么样的原理呢?
杠杆原理:阻力×阻力臂=动力×动力臂
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5 m.
(1)动力F与动力臂l有怎样的函数关系?当动力臂为1.5 m时,撬动石头至少需要多大的力?
(2)若想使动力F不超过题(1)中所用力的一半,则动力臂l至少要加长多少?
解:(1)根据“杠杆原理”,得
Fl=1200×0.5,
所以F关于l的函数解析式为
.
当l=1.5 m时,
(N).
对于函数,当l=1.5 m 时,F=400N,此时杠杆平衡.
因此,撬动石头至少需要400N的力.
(2)当时,
由得
(m),
3-1.5=1.5(m).
对于函数,当l>0时,l越大,F越小.
因此,若想用力不超过400N的一半,则动力臂至少要加长1.5m.
追问:在我们使用撬棍时,为什么动力臂越长越省力?
例题解析
例1 已知反比例函数的图象经过点p(-6,-2).
(1)求出它的表达式;
(2)画出它在第一象限内的图象;
(3)当自变量x从3增大到9时,函数值y是怎样变化的?
例2 如图,它是反比例函数图象的一支,根据图象,回答下列问题:
(1)图象的另一支位于哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点 A(x1,y1)和点B(x2,y2),如果x1>x2,那么y1和y2有怎样的关系?
解:(1)反比例函数的图象只有两种可能:位于第一、第三象限,或者位于第二、第四象限.
∵这个函数的图象的一支位于第一象限,
∴另一支必位于第三象限.
∵这个函数的图象位于第一、第三象限,
∴m-5﹥0,
解得m﹥5.
(2)∵m-5﹥0,
∴在这个函数图象的任一支上,y随x的增大而减小,
∴当x1>x2时,y1﹤y2 .
三、应用提高
1.下列图象中是反比例函数图象的是( )
2.已知反比例函数的图象过点(2,1),则它的图象在________象限,k___0.
3.如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗.
(1)漏斗口的面积S(单位:dm2)与漏斗的深度d有怎样的函数关系?
(2)如果漏斗口的面积为100cm2,则漏斗的深为多少?
答案:(1)(2)30 cm
四、体验收获
说一说你的收获.
1.反比例函数的图象是怎样得到的?画图时要注意什么问题?
2.反比例函数的性质是怎样的?为什么要强调在每一个象限内的性质?
3.在反比例函数图象及性质的应用中体现了数形结合思想,能否谈谈你的体会?
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
