19.4 二次函数的应用 教案

《二次函数的应用》教案
教学目标
一、知识与技能
1．巩固并熟练掌握二次函数的性质．
2．能够运用二次函数的性质解决实际问题．
3．能够分析和表示实际问题中变量之间的二次函数关系，并会运用二次函数求实际问题中的最大值或最小值．增强解决问题的能力．
二、能力目标
建立二次函数模型，进一步体会如何应用二次函数的有关知识解决一些生活实际问题，进而提高理解实际问题、从数学角度抽象分析实际问题和运用数学知识解决实际问题的能力．
三、情感态度与价值观
1．从实际生活中认识到：数学来源于生活，数学服务于生活．
2．培养学生的独立思考的能力和合作学习的精神，在动手、交流过程中培养学生的交际能力和语言表达能力，促进学生综合素质的养成．
3．经历求最大面积的探索过程，体会二次函数是一类最优化问题的数学模型，并感受数学的应用价值．
教学重点
能利用实际问题列出二次函数的解析式，并能利用二次函数的性质求出最大值和最小值．
教学难点
能利用几何图形的有关知识求二次函数的解析式．
教学过程
一、相关知识回顾
1．函数的最值是，是最（填“大”或者“小”）值．
2．说说你是如何做的？
3．将函数化成顶点式，并指出顶点坐标，对称轴．
二、新课引入
1．合作讨论，解决问题：
如图，在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角的边上．
（1）如果设矩形的一边AB=x m，那么AD边的长度如何表示？
（2）设矩形的面积为y m2，当x取何值时，y的值最大？最大值是多少？
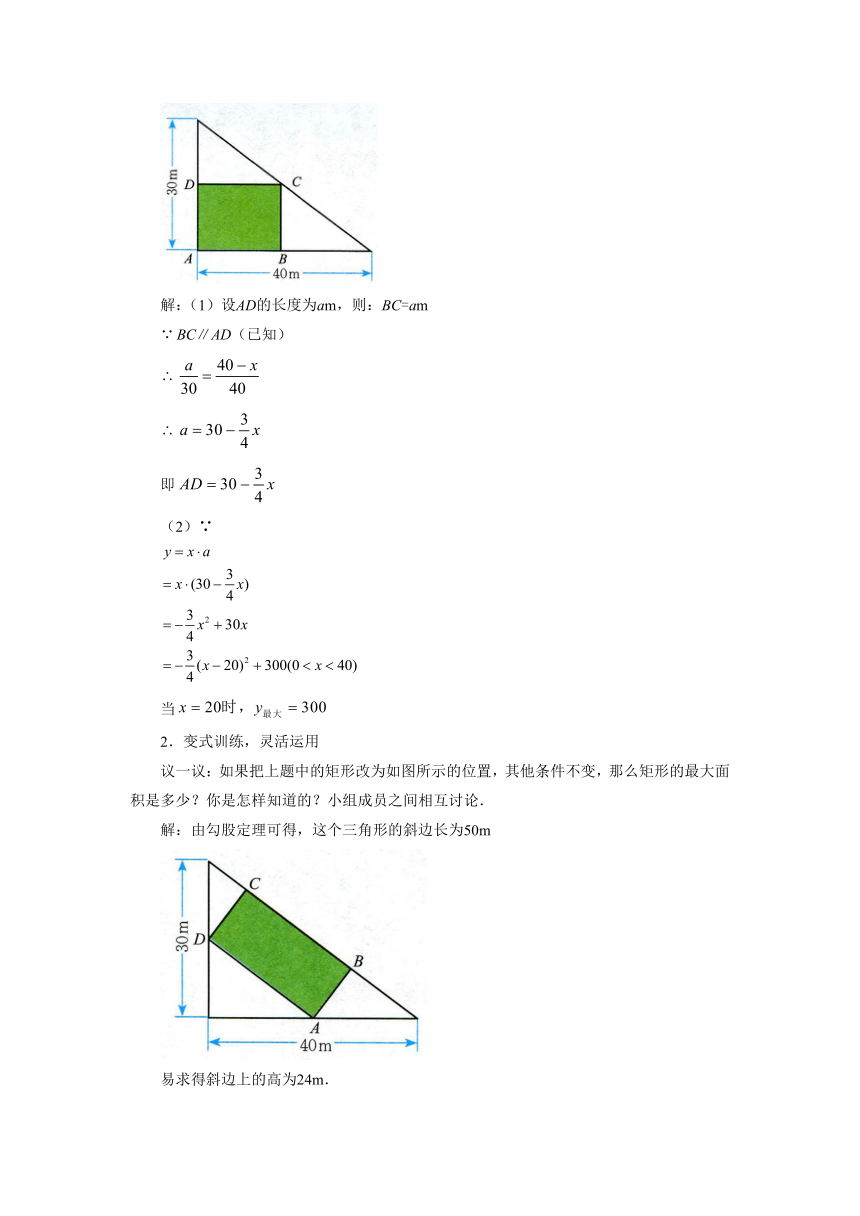
解：（1）设AD的长度为am，则：BC=am
BC∥AD（已知）
即
（2）∵
当
2．变式训练，灵活运用
议一议：如果把上题中的矩形改为如图所示的位置，其他条件不变，那么矩形的最大面积是多少？你是怎样知道的？小组成员之间相互讨论．
解：由勾股定理可得，这个三角形的斜边长为50m
易求得斜边上的高为24m．
设矩形的一边，另一边AB=a m，则有
解得：
所以
因此，当时，
3．归纳总结
解决问题的路和方法整理
（1）数据（常量、变量）提取；
（2）自变量、因变量识别；
（3）构建函数解析式，并求出自变量的取值范围；
（4）利用函数（或图像）的性质求最大（或最小）值．
4．迁移运用，培养能力
例1 利用函数图像求一元二次方程的近似解（精确到0.1）.
例2 某建筑物的窗户如图所示，它的上半部是半圆，下半部是矩形，制造窗框的材料总长（图中所有黑线的长度和）为15m.当x等于多少时，窗户通过的光线最多？（结果精确到0.01m），此时，窗户的面积是多少？
解：
且
设窗户的面积是S m2.则：
当时，
因此，当约为1.07 m时，窗户通过的光线最多，此时窗户的面积约为4.02m2.
例3 某网络玩具店引进一批进价为20元/件的玩具，如果以单价30元销售，那么一个月内可售出180件.根据销售经验，提高单价会导致销售量的下降，即销售单价每上涨1元，月销售量会减少10件.当销售单价为多少时，该店能在一个月内获最大利润？
5．归纳总结，探索规律．
（1）对问题情景中的数量（提取常量、变量）关系进行梳理；
（2）建立函数模型（求出解析式及相应自变量的取值范围等）；
（3）建立函数模型（求出解析式及相应自变量的取值范围等），解决问题用字母（参数）来表示不同数量（如不同长度的线段）间的大小联系.