20.3 用科学计算器求锐角三角函数值 课件(17张PPT)
文档属性
| 名称 | 20.3 用科学计算器求锐角三角函数值 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览



文档简介
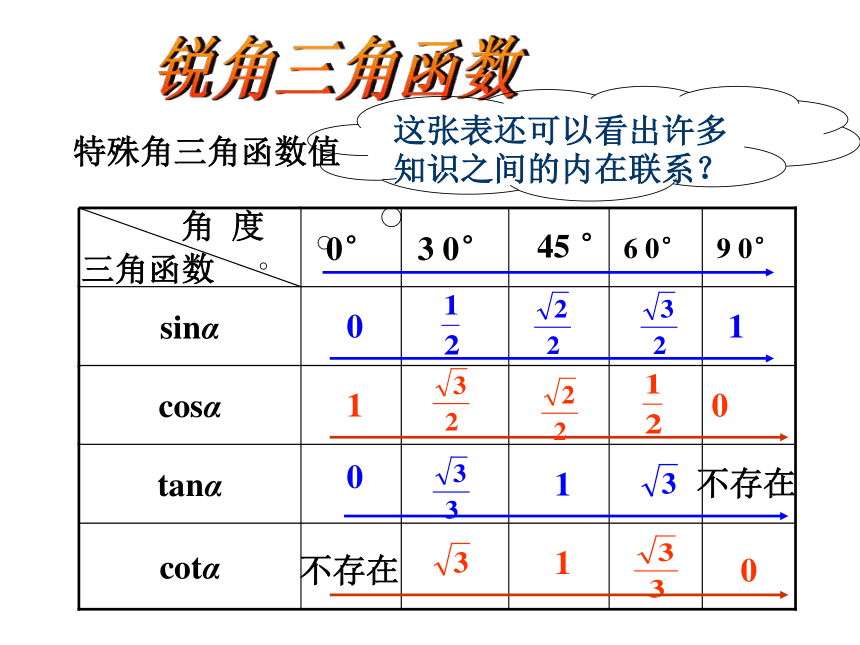
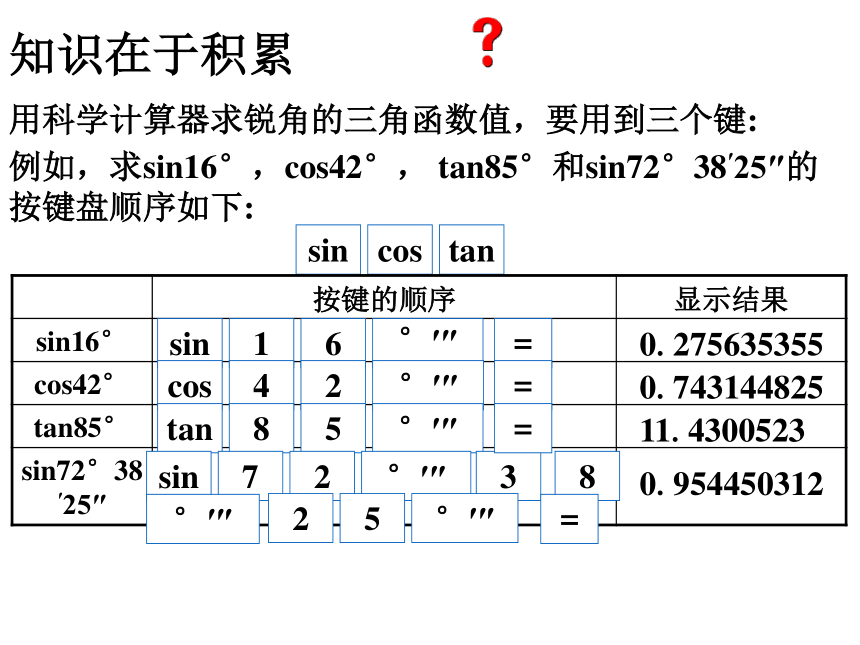
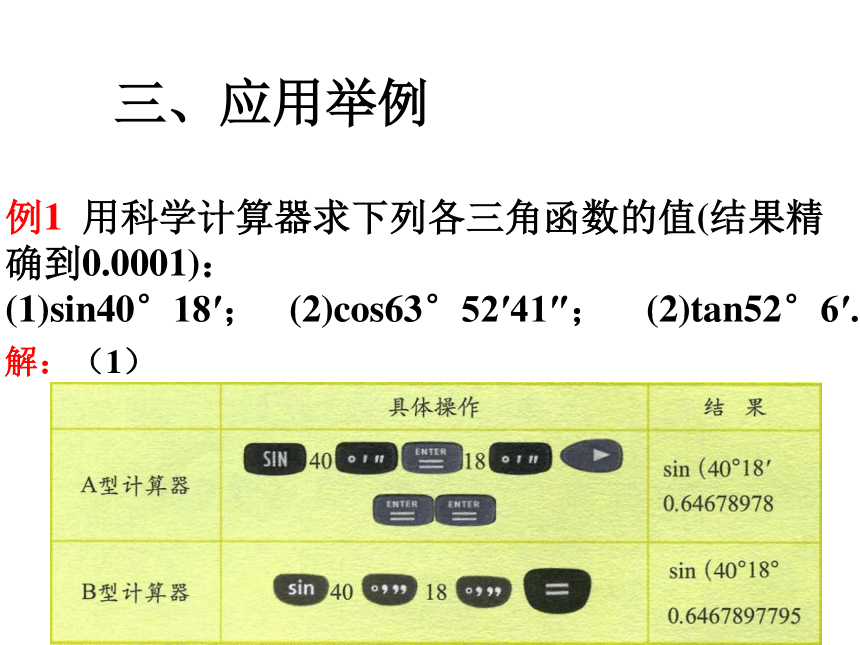
课件17张PPT。用科学计算器求锐角三角函数值 锐角三角函数特殊角三角函数值10011100不存在不存在这张表还可以看出许多知识之间的内在联系?新课引入同学们,前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角(如17°56°89°等)的三角函数值又怎么求呢?这一节课我们就学习借助科学计算器来完成这个任务.这节课我们介绍如何利用计算器求已知锐角的三角函数值和由三角函数值求对应的锐角. 操作探索知识在于积累用科学计算器求锐角的三角函数值,要用到三个键: 例如,求sin16°,cos42°, tan85°和sin72°38′25″的按键盘顺序如下:sin16°′″0.275635355cos42°′″0.743144825tan85°′″11.4300523sin72°′″38°′″25°′″0.954450312====三、应用举例例1 用科学计算器求下列各三角函数的值(结果精确到0.0001):
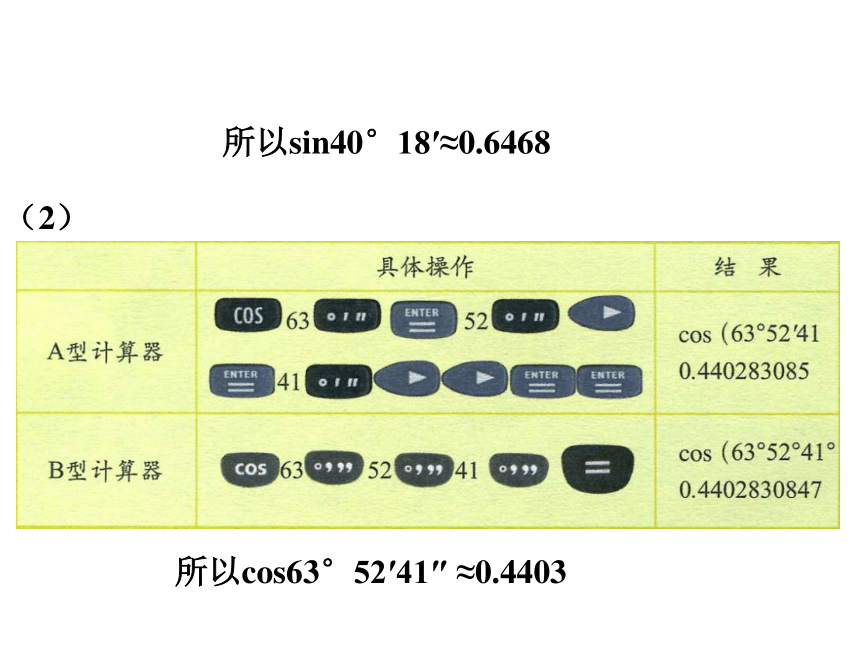
(1)sin40°18′; (2)cos63°52′41″; (2)tan52°6′.解:(1)(2)所以sin40°18′≈0.6468所以cos63°52′41″ ≈0.4403(3)所以tan52°6′ ≈1.28461.用计算器求sin 40°,cos40°,tan40°的值.(精确到0.0001)2.用计算器求下列三角函数值:(精确到0.0001)
(1) sin 72°,cos36°,tan55°;
(2) sin 7°2′25″,cos29°13′44″,tan88°21′.
2.由锐角三角函数值求锐角:例2 已知tan x=0.7410,求锐角x.(精确到1′)解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序依次按键:显示结果为36.538 445 77. 再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.已知cot x=0.1950,求锐角x.(精确到1′)分析 根据tan x= 可以求出tan x的值,然后根据上述方法就可
以求出锐角x的值.x=78°57′57″1.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4174;
(3)tan a=0.1890; 答案: (1)α≈14°20′;(3)α≈10°42′.(2)α≈65°20′;练习:2.用计算器求下式的值.(精确到0.0001)sin81°32′17″+cos38°43′47″答案:1.76923.比较大小:
cos30° cos60°,tan30° tan60°.答案 : ﹥, ﹤探究:用计算器计算:sin36°与cos54°,它们有什么关系?sin24°与cos56°呢?你从中得出什么规律吗?
你能够证明上面的结论吗?四.课堂小结同学们说出:怎样运用自己的科学计算器求出已知锐角的三角函数值和由三角函数值求对应的锐角?
(1)sin40°18′; (2)cos63°52′41″; (2)tan52°6′.解:(1)(2)所以sin40°18′≈0.6468所以cos63°52′41″ ≈0.4403(3)所以tan52°6′ ≈1.28461.用计算器求sin 40°,cos40°,tan40°的值.(精确到0.0001)2.用计算器求下列三角函数值:(精确到0.0001)
(1) sin 72°,cos36°,tan55°;
(2) sin 7°2′25″,cos29°13′44″,tan88°21′.
2.由锐角三角函数值求锐角:例2 已知tan x=0.7410,求锐角x.(精确到1′)解 在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序依次按键:显示结果为36.538 445 77. 再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.已知cot x=0.1950,求锐角x.(精确到1′)分析 根据tan x= 可以求出tan x的值,然后根据上述方法就可
以求出锐角x的值.x=78°57′57″1.已知锐角a的三角函数值,使用计算器求锐角x (精确到1′)
(1)sin a=0.2476; (2)cos a=0.4174;
(3)tan a=0.1890; 答案: (1)α≈14°20′;(3)α≈10°42′.(2)α≈65°20′;练习:2.用计算器求下式的值.(精确到0.0001)sin81°32′17″+cos38°43′47″答案:1.76923.比较大小:
cos30° cos60°,tan30° tan60°.答案 : ﹥, ﹤探究:用计算器计算:sin36°与cos54°,它们有什么关系?sin24°与cos56°呢?你从中得出什么规律吗?
你能够证明上面的结论吗?四.课堂小结同学们说出:怎样运用自己的科学计算器求出已知锐角的三角函数值和由三角函数值求对应的锐角?
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
