20.1 锐角三角函数 课件(16张PPT)
文档属性
| 名称 | 20.1 锐角三角函数 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 455.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览






文档简介
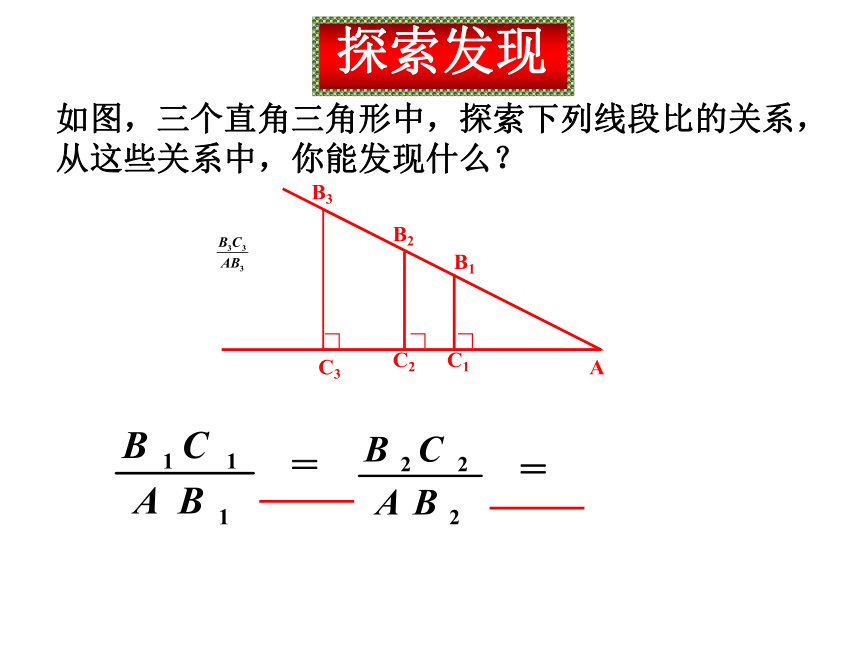
课件16张PPT。锐角三角函数 探索发现如图,三个直角三角形中,探索下列线段比的关系,从这些关系中,你能发现什么?==在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即解:在Rt△ABC中, ∠C=90°,AC=3,BC=4,由勾股定理,得 例题解析例1 已知:如图20-5,在Rt△ABC中,∠C=90°,AC=3,BC=4,求sinA和sinB的值.
图20-5例2 已知:如图20-6,在△ABC中,CD是AB边上的高, CD=12, AD=9,BD=5, 求sin A,sin ∠ACD,sinB和sin ∠BCD的值.
解:在△ABC中, CD是AB边上的高, 图20-6∴ ∠ADC=∠BDC=90°.在Rt△ADC中,AD=9,CD=12,由勾股定理,得 在Rt△BCD中,BD=5,CD=12,由勾股定理,得 ∴sinB=________=_______, sin ∠BCD =________=_______.在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.抽象概括在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦、余弦和正切都是∠A的三角函数.在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即例3 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.咋办老师提示:过点A作AD⊥BC于D.解:过A作AD⊥BC于D,例4 已知:如图20-10,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=16,BC=12,求sin ∠DCA和tan ∠DCA的值.
图20-10解:∵∠ACB=90°,AB=16,BC=12,又CD⊥AB于点D,∴∠DCA=∠B.随堂练习1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 求AB,sinB.2.如图:在Rt△ABC中,∠C=90°,AC=10,随堂练习3.在Rt△ABC中,∠C=90°,BC=20,
求△ABC的周长和面积.解:在Rt△ABC中,随堂练习4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,A的三个三角函数的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定C随堂练习4.如图, ∠C=90°CD⊥AB.( ) ( ) ( )CD
BCAC
ABAD
AC( ) ( ) ( )锐角三角函数定义:请思考:在Rt△ABC中, ∠C=90°sinA和cosB有什么关系? 回味无穷sinA=cosB∠A的对边
图20-5例2 已知:如图20-6,在△ABC中,CD是AB边上的高, CD=12, AD=9,BD=5, 求sin A,sin ∠ACD,sinB和sin ∠BCD的值.
解:在△ABC中, CD是AB边上的高, 图20-6∴ ∠ADC=∠BDC=90°.在Rt△ADC中,AD=9,CD=12,由勾股定理,得 在Rt△BCD中,BD=5,CD=12,由勾股定理,得 ∴sinB=________=_______, sin ∠BCD =________=_______.在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.抽象概括在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦、余弦和正切都是∠A的三角函数.在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即例3 如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.咋办老师提示:过点A作AD⊥BC于D.解:过A作AD⊥BC于D,例4 已知:如图20-10,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=16,BC=12,求sin ∠DCA和tan ∠DCA的值.
图20-10解:∵∠ACB=90°,AB=16,BC=12,又CD⊥AB于点D,∴∠DCA=∠B.随堂练习1.如图,△ABC是等腰直角三角形,你能根据图中所给数据求出tanC吗? 求AB,sinB.2.如图:在Rt△ABC中,∠C=90°,AC=10,随堂练习3.在Rt△ABC中,∠C=90°,BC=20,
求△ABC的周长和面积.解:在Rt△ABC中,随堂练习4.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,A的三个三角函数的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定C随堂练习4.如图, ∠C=90°CD⊥AB.( ) ( ) ( )CD
BCAC
ABAD
AC( ) ( ) ( )锐角三角函数定义:请思考:在Rt△ABC中, ∠C=90°sinA和cosB有什么关系? 回味无穷sinA=cosB∠A的对边
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
