21.3 圆的对称性 课件(23张PPT)
文档属性
| 名称 | 21.3 圆的对称性 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 00:00:00 | ||
图片预览



文档简介
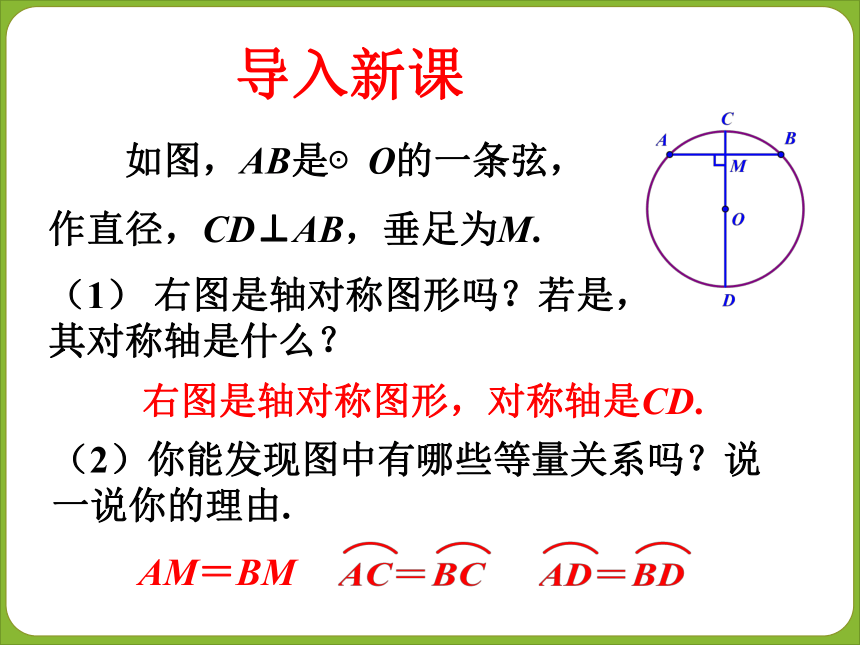
课件23张PPT。圆的对称性 如图,AB是⊙O的一条弦,作直径,CD⊥AB,垂足为M.(1) 右图是轴对称图形吗?若是,其对称轴是什么?(2)你能发现图中有哪些等量关系吗?说一说你的理由.右图是轴对称图形,对称轴是CD.AM=BM导入新课 垂直于弦的直径平分这条弦,并且平分弦所对的弧.几何语言叙述定理:∵CD为⊙O的直径,且CD⊥AB,
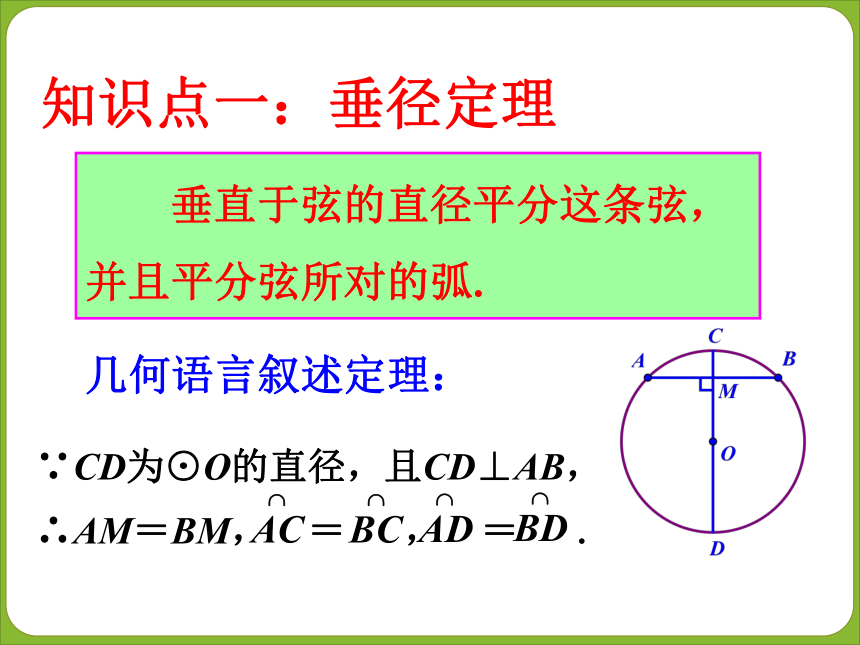
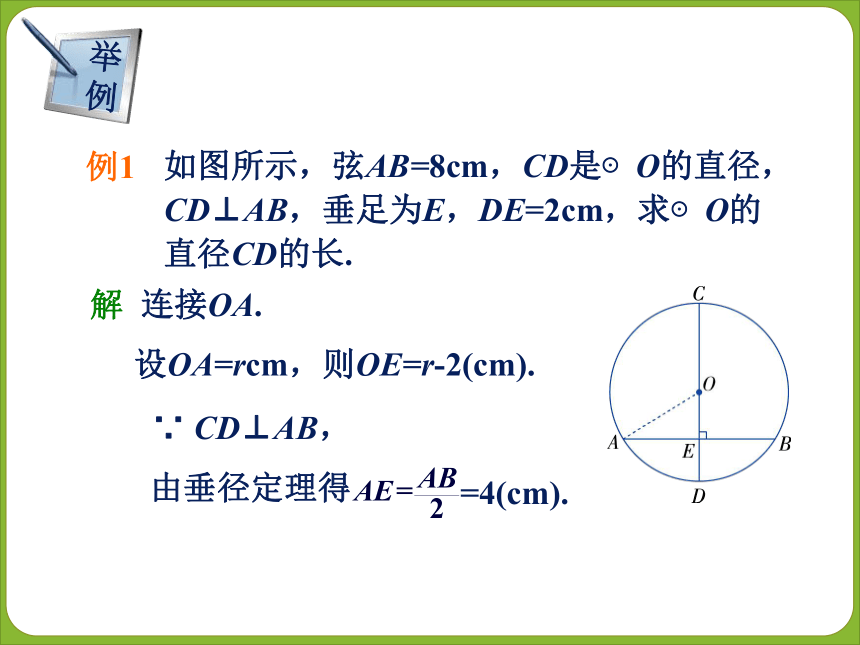
∴AM=BM, = , = . 知识点一:垂径定理 解 连接OA.设OA=rcm,则OE=r-2(cm).∵ CD⊥AB,解得 r=5. ∴ CD = 2r = 10 (cm). 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.几何语言叙述定理:知识点二:垂径定理的逆定理∵AM = BM,CD为⊙O的直径,
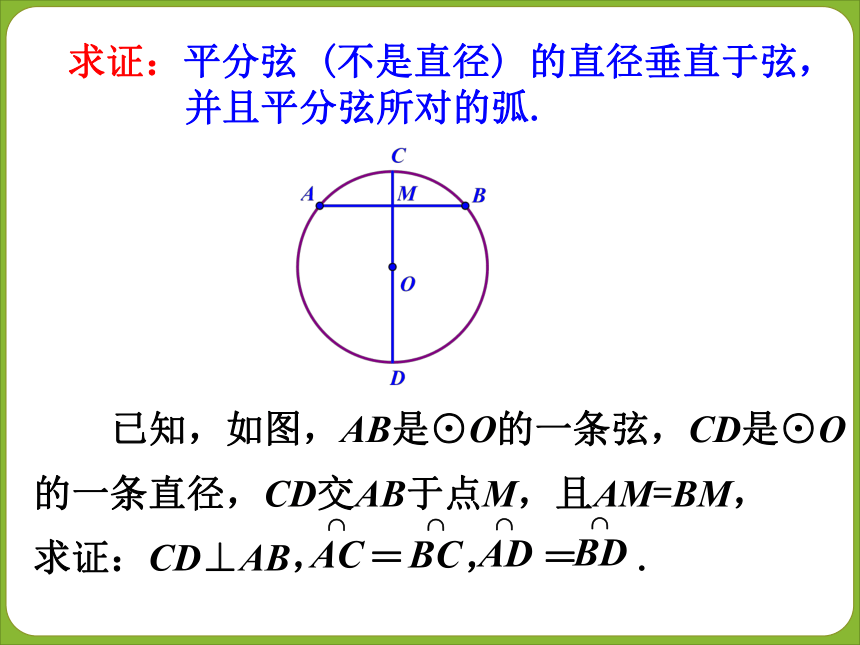
∴CD⊥AB, = , = . 求证:平分弦 (不是直径) 的直径垂直于弦,
并且平分弦所对的弧. 已知,如图,AB是⊙O的一条弦,CD是⊙O
的一条直径,CD交AB于点M,且AM=BM,
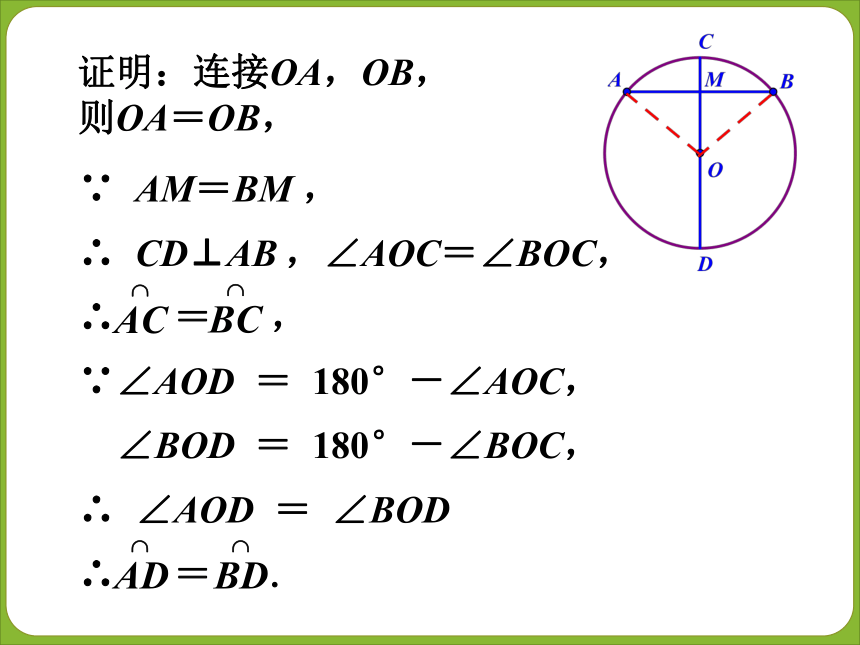
求证:CD⊥AB, = , = .∵ AM=BM ,
∴ CD⊥AB ,∠AOC=∠BOC,
∴ = ,
∵∠AOD = 180°-∠AOC,
∠BOD = 180°-∠BOC,
∴ ∠AOD = ∠BOD
∴ = .证明:连接OA,OB,
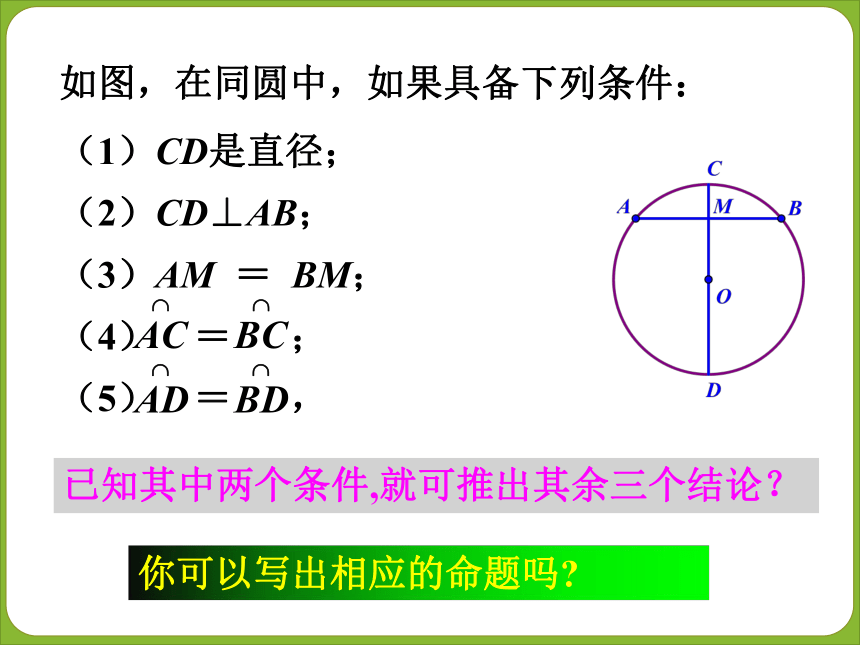
则OA=OB,你可以写出相应的命题吗?已知其中两个条件,就可推出其余三个结论?如图,在同圆中,如果具备下列条件:(1)CD是直径;
(2)CD⊥AB;
(3)AM = BM;
(4) = ;
(5) = ,证明 作直径EF⊥AB,又 AB∥CD,EF⊥AB,∴ EF⊥CD.∵AD=37.4,DC= 7.2,OD=OC- DC=R-7.2.在Rt△OAD中,由勾股定理,得:
OA2 =AD2+OD2.答:桥拱所在圆的半径约为27.9m.解这个方程,得R≈27.9(m).即R2 =18.72+(R-7.2)2. 如图,⊙O的半径为 5cm,弦 AB为 6cm.求圆心 O 到弦 AB 的距离. 本例为垂径定理的应用。利用圆中常规辅助线“过圆心作弦的垂线”,与圆半径、弦,构成直角三角形,再利用解直角三角形的知识求解.随堂检测点拨:解:连接OA,过圆心O作
OE⊥AB于E,则: 如图,⊙O的半径为 5cm,弦 AB为 6cm.求圆心 O 到弦 AB 的距离.做一做1.已知,⊙O的半径为2cm,弦AB为2 cm,
求弦AB中点到它所对劣弧中点的距离.解:连接OA,过点O作OC⊥AB
于点C,延长OC交圆周于点D.则:
AC= AB= ×2 = (cm)在Rt△AOC中,有: OA=2cm,AC= cm
由勾股定理,得:OC2+AC2=OA2,
∴OC= = =1(cm),
∴CD=OD-OC=OA-OC=2-1=1(cm).即弦AB中点到它所对劣弧中点距离为1cm.2.已知:AB是⊙O的直径,AC、AD是在AB两侧的两条弦,且AC=AD.
求证:AB平分∠CAD.解:过点O作OE⊥AC于E
OF⊥AD于F.由垂径定理,可得:AE= AC,AF= AD
∵AC=AD,∴AE=AF,
在Rt△AOE和Rt△AOF中:OA=OA,AE=AF,
∴ Rt△AOE≌Rt△AOF,∴∠OAE=∠OAF,
即AB平分∠CAD.思考:圆是中心对称图形吗?如果是,它的对称中心是什么?你能找到对称中心吗?你又是用什么方法解决这个问题的呢?·圆是中心对称图形;圆心是它的对称中心;用旋转的方法解决这个问题.圆的中心对称性 一个圆绕着它的圆心旋转任意一个角度,
还能与原来的图形重合吗?结论1:一个圆绕着它的圆心旋转任意一个角
度,都能与原来的图形重合,我们把
圆的这个特性称之为圆的旋转不变性.
结论2:圆是中心对称图形,对称中心为圆心.圆心角、弧、弦之间的关系 在等圆⊙O和⊙O′中,分别作相等的圆心
角∠AOB和∠A ′OB ′(如图3-8),将两圆重叠,
并固定圆心,然后把其中的一个圆旋转一
个角度,得OA与OA′重合.你能发现哪些等量关系?说一说你的理由?例4已知:A,B是⊙O上的两点,∠AOB=120°,
C是 的中点.试判断四边形AOBC的形状,并说明理由.解:四边形AOBC为菱形.例题讲解∴四边形AOBC为菱形.理由如下:如图21-26,连接OC.∵∠AOB=120°,又∵OA=OC=OB ,∴△AOC,△BOC均为等边三角形.∴AC=AO=BO =BC.谢 谢
∴AM=BM, = , = . 知识点一:垂径定理 解 连接OA.设OA=rcm,则OE=r-2(cm).∵ CD⊥AB,解得 r=5. ∴ CD = 2r = 10 (cm). 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.几何语言叙述定理:知识点二:垂径定理的逆定理∵AM = BM,CD为⊙O的直径,
∴CD⊥AB, = , = . 求证:平分弦 (不是直径) 的直径垂直于弦,
并且平分弦所对的弧. 已知,如图,AB是⊙O的一条弦,CD是⊙O
的一条直径,CD交AB于点M,且AM=BM,
求证:CD⊥AB, = , = .∵ AM=BM ,
∴ CD⊥AB ,∠AOC=∠BOC,
∴ = ,
∵∠AOD = 180°-∠AOC,
∠BOD = 180°-∠BOC,
∴ ∠AOD = ∠BOD
∴ = .证明:连接OA,OB,
则OA=OB,你可以写出相应的命题吗?已知其中两个条件,就可推出其余三个结论?如图,在同圆中,如果具备下列条件:(1)CD是直径;
(2)CD⊥AB;
(3)AM = BM;
(4) = ;
(5) = ,证明 作直径EF⊥AB,又 AB∥CD,EF⊥AB,∴ EF⊥CD.∵AD=37.4,DC= 7.2,OD=OC- DC=R-7.2.在Rt△OAD中,由勾股定理,得:
OA2 =AD2+OD2.答:桥拱所在圆的半径约为27.9m.解这个方程,得R≈27.9(m).即R2 =18.72+(R-7.2)2. 如图,⊙O的半径为 5cm,弦 AB为 6cm.求圆心 O 到弦 AB 的距离. 本例为垂径定理的应用。利用圆中常规辅助线“过圆心作弦的垂线”,与圆半径、弦,构成直角三角形,再利用解直角三角形的知识求解.随堂检测点拨:解:连接OA,过圆心O作
OE⊥AB于E,则: 如图,⊙O的半径为 5cm,弦 AB为 6cm.求圆心 O 到弦 AB 的距离.做一做1.已知,⊙O的半径为2cm,弦AB为2 cm,
求弦AB中点到它所对劣弧中点的距离.解:连接OA,过点O作OC⊥AB
于点C,延长OC交圆周于点D.则:
AC= AB= ×2 = (cm)在Rt△AOC中,有: OA=2cm,AC= cm
由勾股定理,得:OC2+AC2=OA2,
∴OC= = =1(cm),
∴CD=OD-OC=OA-OC=2-1=1(cm).即弦AB中点到它所对劣弧中点距离为1cm.2.已知:AB是⊙O的直径,AC、AD是在AB两侧的两条弦,且AC=AD.
求证:AB平分∠CAD.解:过点O作OE⊥AC于E
OF⊥AD于F.由垂径定理,可得:AE= AC,AF= AD
∵AC=AD,∴AE=AF,
在Rt△AOE和Rt△AOF中:OA=OA,AE=AF,
∴ Rt△AOE≌Rt△AOF,∴∠OAE=∠OAF,
即AB平分∠CAD.思考:圆是中心对称图形吗?如果是,它的对称中心是什么?你能找到对称中心吗?你又是用什么方法解决这个问题的呢?·圆是中心对称图形;圆心是它的对称中心;用旋转的方法解决这个问题.圆的中心对称性 一个圆绕着它的圆心旋转任意一个角度,
还能与原来的图形重合吗?结论1:一个圆绕着它的圆心旋转任意一个角
度,都能与原来的图形重合,我们把
圆的这个特性称之为圆的旋转不变性.
结论2:圆是中心对称图形,对称中心为圆心.圆心角、弧、弦之间的关系 在等圆⊙O和⊙O′中,分别作相等的圆心
角∠AOB和∠A ′OB ′(如图3-8),将两圆重叠,
并固定圆心,然后把其中的一个圆旋转一
个角度,得OA与OA′重合.你能发现哪些等量关系?说一说你的理由?例4已知:A,B是⊙O上的两点,∠AOB=120°,
C是 的中点.试判断四边形AOBC的形状,并说明理由.解:四边形AOBC为菱形.例题讲解∴四边形AOBC为菱形.理由如下:如图21-26,连接OC.∵∠AOB=120°,又∵OA=OC=OB ,∴△AOC,△BOC均为等边三角形.∴AC=AO=BO =BC.谢 谢
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
