20.4 解直角三角形 课件(18张PPT)
文档属性
| 名称 | 20.4 解直角三角形 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 16:57:44 | ||
图片预览






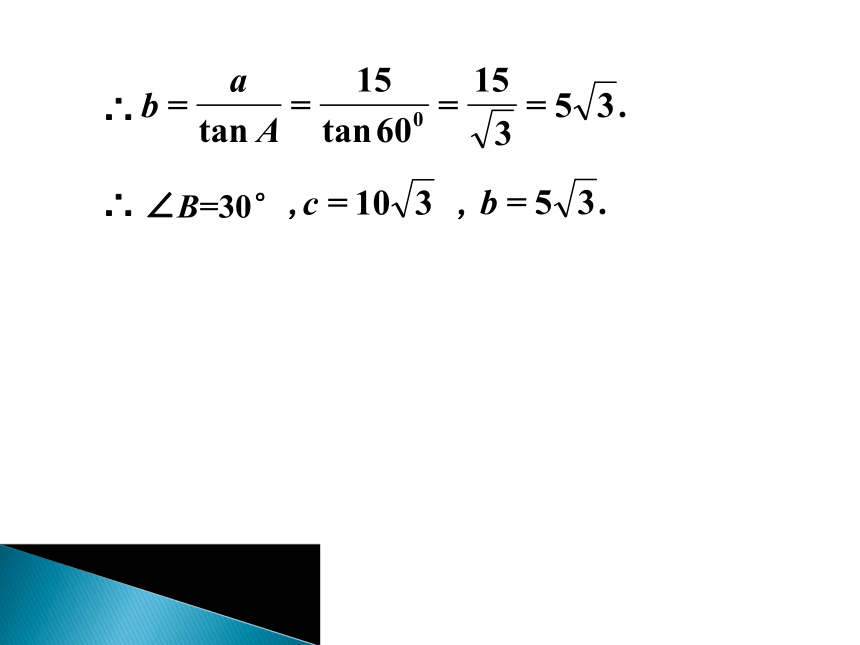
文档简介
课件18张PPT。在直角三角形中,除直角外,还有哪些元素?
这5个元素之间有什么关系?
知道其中哪些元素,可以求出其余的元素?思考与探索在Rt△ABC中,∠C为直角,其余5个元素之间有以下关系:(2)锐角之间的关系:
∠A+ ∠B=90°(直角三角形的两个锐角互余)(1)三边之间关系:(3)边角之间的关系: 由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.例题分析例1 在Rt△ABC中,∠C=90°,∠A=60°,a=15.解这个直角三角形.基础练习在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.(1) a=9, b=6;(2) ∠A = 18 °, c=13.解:∴∠A=45°,∠B =45°且a=b又∵ a+b=4∴a=b=2例题分析例4 已知:如图20-15,在△ABC中,AB=AC,∠A=120°,BC=4cm,求AB的长.解:作AD⊥BC于D,则∠ADB=90°.∵AB=AC,∠BAC=120°,D∵ BC=4cm ,∴BD=2cm.在Rt△ABD中,在Rt△ABC中,CD是斜边上的高.
若AC=8,cosA=0.8,求△ABC的面积.随堂练习如图,在△ABC中,∠ACB=90°,
BC=15cm,∠BAC=30°,∠DAC=45°,
求AD.ACBD能力提升在山脚C处测得山顶A的仰角为450.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB.DEFx变式训练1、通过做适当的辅助线,构造直角三角形.
2、有公共直角边的两个直角三角形,一般设出公共边的长度(x米)在另一个直角三角形中根据锐角三角函数关系列出程.
3、测量底部不能到达的物体的高度,通常选用这种方法.归纳总结已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.优选关系式
这5个元素之间有什么关系?
知道其中哪些元素,可以求出其余的元素?思考与探索在Rt△ABC中,∠C为直角,其余5个元素之间有以下关系:(2)锐角之间的关系:
∠A+ ∠B=90°(直角三角形的两个锐角互余)(1)三边之间关系:(3)边角之间的关系: 由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形.利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素.例题分析例1 在Rt△ABC中,∠C=90°,∠A=60°,a=15.解这个直角三角形.基础练习在Rt△ABC中,∠C=90°,a、b、c分别为
∠A 、∠B、 ∠C的对边.根据已知条件,
解直角三角形.(1) a=9, b=6;(2) ∠A = 18 °, c=13.解:∴∠A=45°,∠B =45°且a=b又∵ a+b=4∴a=b=2例题分析例4 已知:如图20-15,在△ABC中,AB=AC,∠A=120°,BC=4cm,求AB的长.解:作AD⊥BC于D,则∠ADB=90°.∵AB=AC,∠BAC=120°,D∵ BC=4cm ,∴BD=2cm.在Rt△ABD中,在Rt△ABC中,CD是斜边上的高.
若AC=8,cosA=0.8,求△ABC的面积.随堂练习如图,在△ABC中,∠ACB=90°,
BC=15cm,∠BAC=30°,∠DAC=45°,
求AD.ACBD能力提升在山脚C处测得山顶A的仰角为450.沿着坡角为30 °的斜坡前进300米到达D点,在D点测得山顶A的仰角为600 ,求山高AB.DEFx变式训练1、通过做适当的辅助线,构造直角三角形.
2、有公共直角边的两个直角三角形,一般设出公共边的长度(x米)在另一个直角三角形中根据锐角三角函数关系列出程.
3、测量底部不能到达的物体的高度,通常选用这种方法.归纳总结已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.优选关系式
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
