20.5 测量与计算 课件(17张PPT)
文档属性
| 名称 | 20.5 测量与计算 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 973.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 16:57:44 | ||
图片预览



文档简介
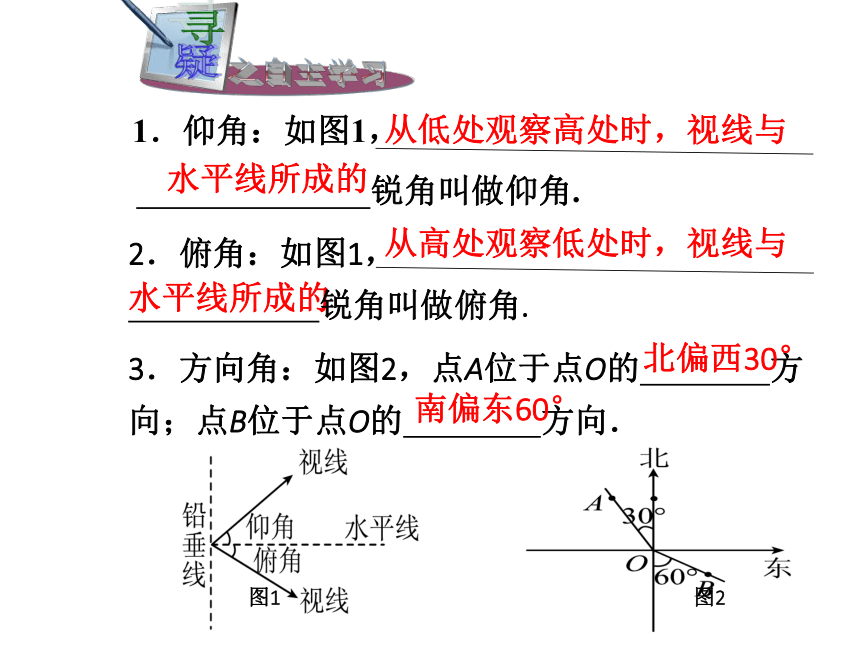
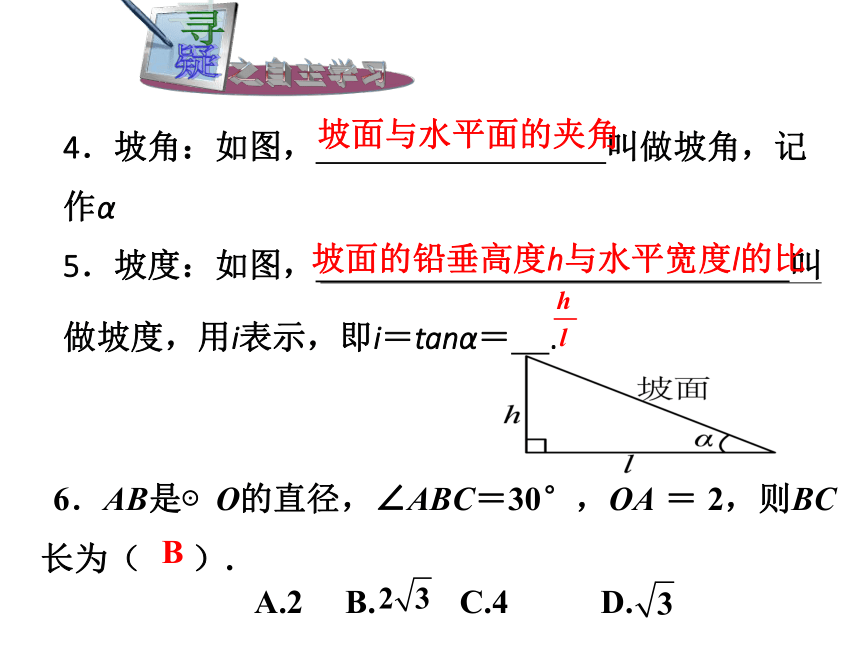
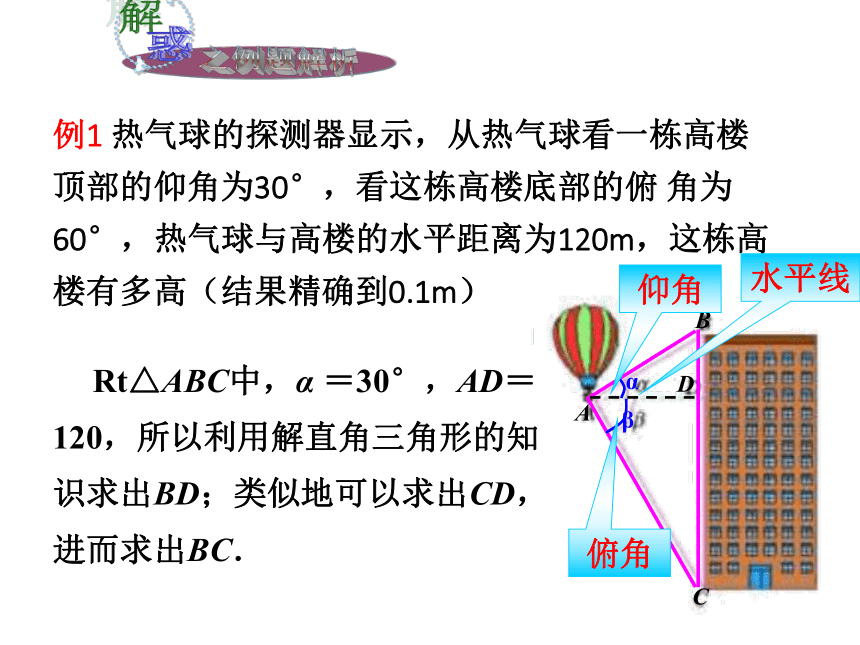
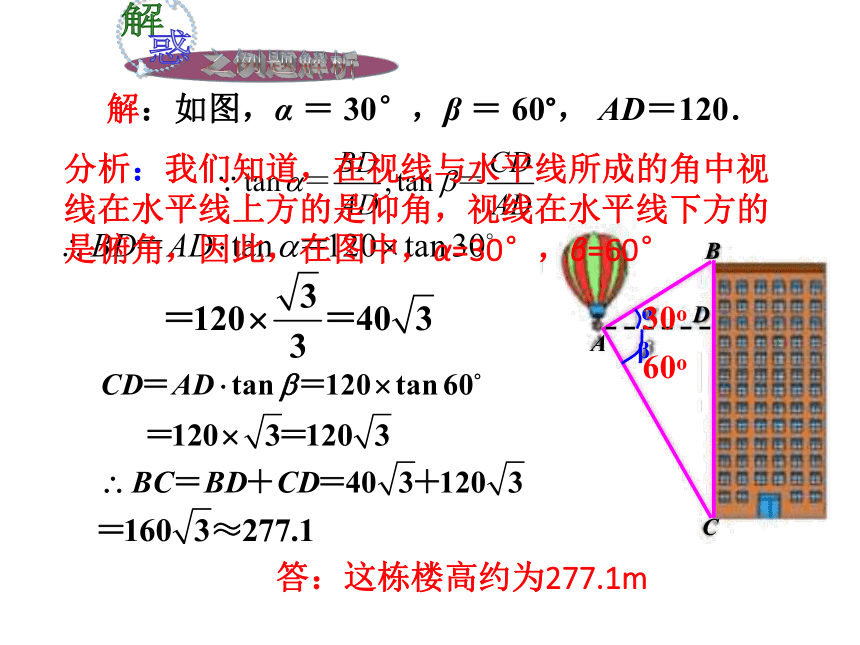
课件17张PPT。测量与计算从低处观察高处时,视线与从高处观察低处时,视线与3.方向角:如图2,点A位于点O的 方向;点B位于点O的 方向.北偏西30° 南偏东60°水平线所成的水平线所成的图1图24.坡角:如图, 叫做坡角,记作α坡面与水平面的夹角坡面的铅垂高度h与水平宽度l的比 6.AB是⊙O的直径,∠ABC=30°,OA = 2,则BC长为( ). A.2 B. C.4 D.B例1 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m) Rt△ABC中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.仰角水平线俯角解:如图,α = 30°,β = 60°, AD=120.答:这栋楼高约为277.1m分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,α=30°,β=60°30o60o例2 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到1海里)解析:首先根据题意得出∠APC=90°-65°=25°,再利用解直角三角形求出即可.解:如图,在Rt△APC中,∠APC=90°-65° = 25°∴PC=PA?cos∠APC≈80×0.91 = 72.505在Rt△BPC中,∠B = 34°答:海轮所在的B处距离灯塔P约有130海里.例3 如图, 一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发, 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度? 小刚上升了多少米? (角度精确到0.01°,长度精确到0.1 m)●●解析:在直角三角形ABC中,已知了坡度即角α的正切可求出坡角α,然后用α的正弦求出对边BC的长.例3 如图, 一山坡的坡度为i = 1∶2 . 小刚从山脚A 出发, 沿山坡向上走了240 m 到达点C. 这座山坡的坡角是多少度? 小刚上升了多少米? (角度精确到0.01°,长度精确到0.1 m)解:用α 表示坡角的大小,由题意可得
因此α ≈26.57° 在Rt△ABC中, ∠B =90°, ∠A = 26.57°, AC = 240
因此 BC = 240 ×sin26.57°≈107.3(m)
答:这座山坡的坡角约为26.57 °,小刚上升了约107.3 m.例4 在数学活动课上,老师带领学生去测量位于北京大学未名湖东南湖畔的博雅塔的高度.如图20-22,在C处用高1.2m的测角仪CE测得塔顶A的仰角为300,向它的方向前进50m到达D处,在D处测得塔顶A的仰角为710.求博雅塔的高AB约为多少米(结果精确到1m).分析:设EF的延长线交AB于点G,根据题意,要求AB的长,只要求出AG的长即可.设AG为xm,在Rt△AEG和Rt △ AFG中,EG和FG分别能用含x的代数式表示,再利用EG-FG=EF,得到关于x的方程,进而求得x的值. 解:设EF的延长线交AB于点G,根据题意,得DF=BG=CE=1.2,EF=CD=50.设AG为xm,在Rt△AEG和Rt △ AFG中,∵∠AEF=30°, ∠AFG=71°,∴∠EAG=60°, ∠FAG=19°.∴EG=AG· tan∠EAG =x · tan60°.同理FG=AG· tan∠FAG =x · tan19°.又EF=EG-FG,∴50=( tan60° -tan19°) · x .∴AB=AG+GB=36.0+1.2=37.2 ≈37(米)答:博雅塔的高AB约为37米.1.如图,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C2.如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD = 200m,点C在BD上,则树高AB等于 (根号保留).3.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.244.如图7,河堤横断面是梯形,上底为4 m,堤高为6 m,斜坡AD的坡比为1∶3,斜坡BC的坡角为45 °,则河堤的横断面积是( )A.96 m2 B.48 m2
C.192 m2 D. 84 m2 A请谈谈你的收获小组合作讨论
因此α ≈26.57° 在Rt△ABC中, ∠B =90°, ∠A = 26.57°, AC = 240
因此 BC = 240 ×sin26.57°≈107.3(m)
答:这座山坡的坡角约为26.57 °,小刚上升了约107.3 m.例4 在数学活动课上,老师带领学生去测量位于北京大学未名湖东南湖畔的博雅塔的高度.如图20-22,在C处用高1.2m的测角仪CE测得塔顶A的仰角为300,向它的方向前进50m到达D处,在D处测得塔顶A的仰角为710.求博雅塔的高AB约为多少米(结果精确到1m).分析:设EF的延长线交AB于点G,根据题意,要求AB的长,只要求出AG的长即可.设AG为xm,在Rt△AEG和Rt △ AFG中,EG和FG分别能用含x的代数式表示,再利用EG-FG=EF,得到关于x的方程,进而求得x的值. 解:设EF的延长线交AB于点G,根据题意,得DF=BG=CE=1.2,EF=CD=50.设AG为xm,在Rt△AEG和Rt △ AFG中,∵∠AEF=30°, ∠AFG=71°,∴∠EAG=60°, ∠FAG=19°.∴EG=AG· tan∠EAG =x · tan60°.同理FG=AG· tan∠FAG =x · tan19°.又EF=EG-FG,∴50=( tan60° -tan19°) · x .∴AB=AG+GB=36.0+1.2=37.2 ≈37(米)答:博雅塔的高AB约为37米.1.如图,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C2.如图,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD = 200m,点C在BD上,则树高AB等于 (根号保留).3.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 海里.244.如图7,河堤横断面是梯形,上底为4 m,堤高为6 m,斜坡AD的坡比为1∶3,斜坡BC的坡角为45 °,则河堤的横断面积是( )A.96 m2 B.48 m2
C.192 m2 D. 84 m2 A请谈谈你的收获小组合作讨论
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
