21.1 圆的有关概念 课件(41张PPT)
文档属性
| 名称 | 21.1 圆的有关概念 课件(41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 16:57:44 | ||
图片预览









文档简介
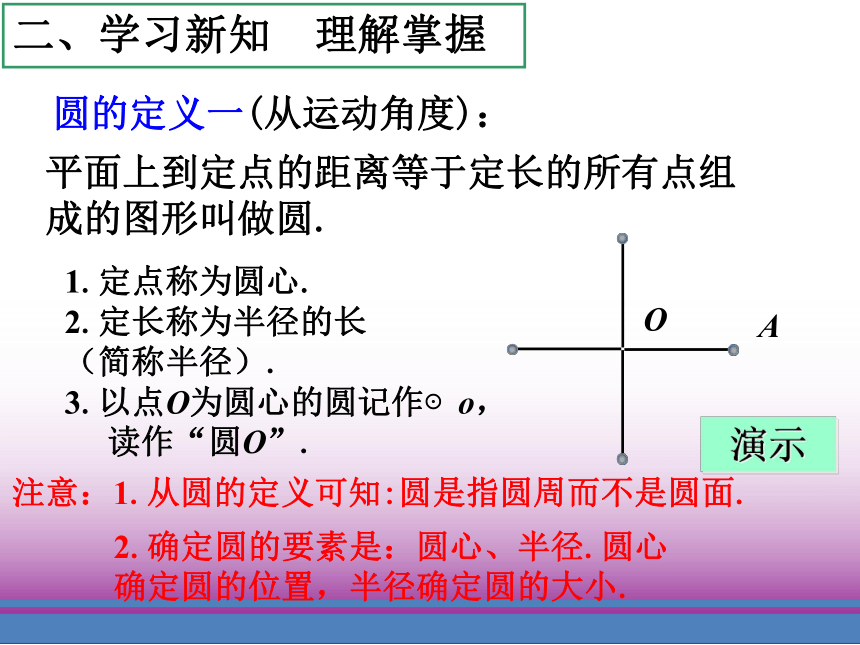
课件41张PPT。圆的有关概念一、创设情境 引入新课平面上到定点的距离等于定长的所有点组成的图形叫做圆.注意:1.从圆的定义可知:圆是指圆周而不是圆面.2.确定圆的要素是:圆心、半径.圆心确定圆的位置,半径确定圆的大小.1.定点称为圆心.
2.定长称为半径的长
(简称半径).
3.以点O为圆心的圆记作⊙o,读作“圆O”.圆的定义一(从运动角度):演示OA二、学习新知 理解掌握试根据圆的定义填空:
1、圆上各点到 的距离都等 于 .
2、到定点的距离等于定长的点都在 .定点(圆心)定长(半径的长)圆上定义二:圆是到定点的距离等于定长的点的集合.圆的内部:
可以看作是到圆心的距离小于半径的点的集合.
圆的外部:
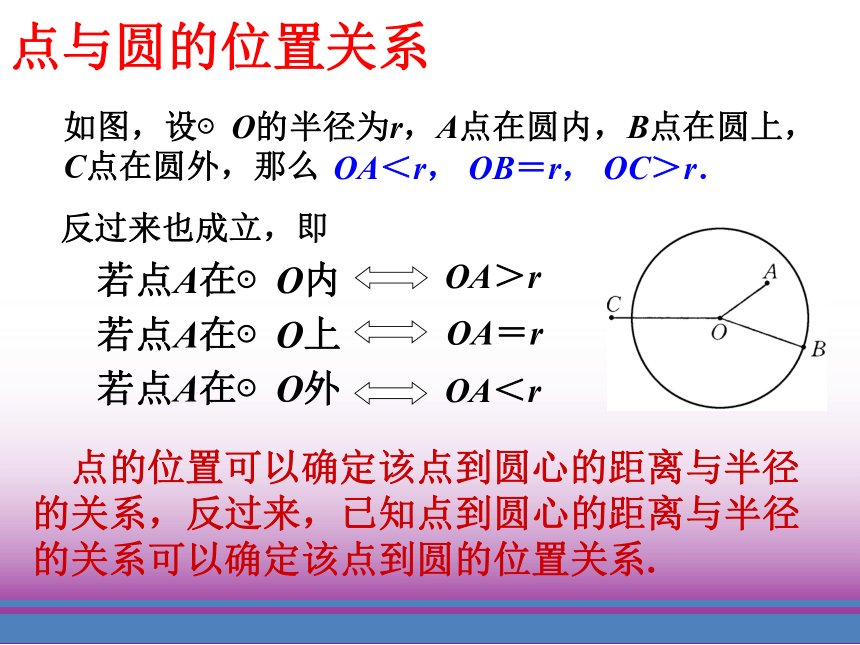
可以看作是到圆心的距离大于半径的点的集合.圆的定义二(从集合角度):提问: 如果一个点到圆心距离小于半径, 那么这个点在哪里呢? 大于圆的半径呢? 反过来呢? 点与圆的位置关系点与圆的位置关系如图,设⊙O的半径为r,A点在圆内,B点在圆上,
C点在圆外,那么OA<r, OB=r, OC>r.反过来也成立,即 点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系.想一想:如图所示, ⊙O是一个半径为r的圆.在圆内、圆外、圆
上分别取一点,点到圆心的距离为d,请用r与d的大小
来刻画它们的位置特征.点与圆位置关系有三种:点在圆外、点在圆上、点在圆内点在圆外,即d > r;
点在圆上,即d = r;
点在圆外,即d < r..O 车轮为什么做成圆形?三、学以致用 应用新知车轮做成三角形、正方形可以吗?如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?C表示车轮边缘上的任意一点.
要使车轮能够平稳地滚动,C,
O之间的距离与A,O之间的距
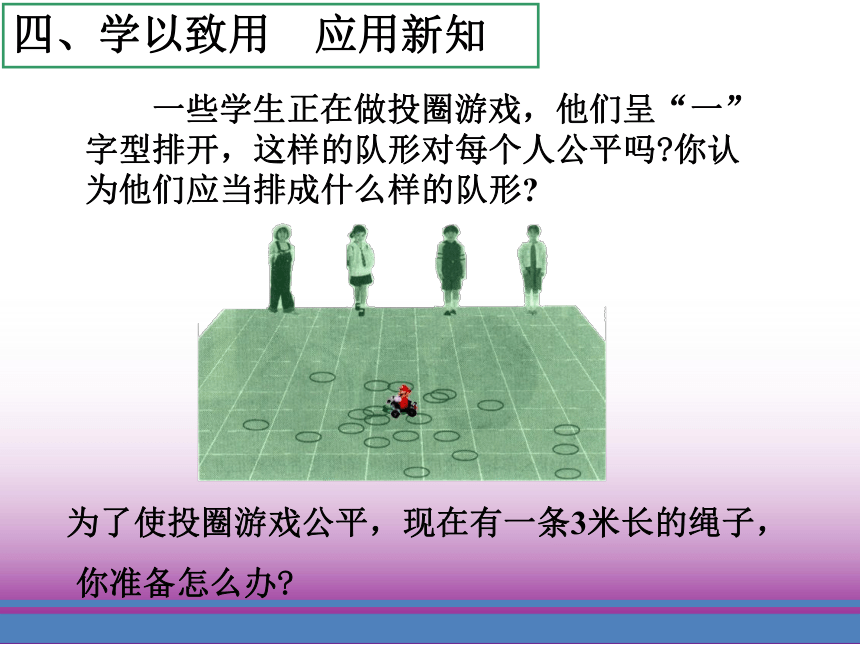
离应满足什么关系?车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.为了使投圈游戏公平,现在有一条3米长的绳子,
你准备怎么办? 四、学以致用 应用新知五、例题分析 运用新知例1 在△ABC中,∠C=900,AC=4,AB=5,以点C为圆心,以r为半径作圆,按下列条件分别判断A,B两点和⊙C的位置关系:(1) r=2.4 (2) r=4 解:∵∠C=900,AC=4,AB=5,(1) r=2.4时,∵BC=3>r ,AC=4>r ,∴A,B两点都在⊙C外.(2) r=4时,∵BC=3<r ,AC=4=r ,∴点B在⊙C内,点A在⊙C上.例2 已知四边形ABCD为矩形.试判断A,B,C,D四个点是否在同一个圆上,并说明理由.解: A,B,C,D四个点在同一个圆上.如图21-3,连接AC,BD,AC与BD相交于O.理由如下:∵四边形ABCD为矩形.又∵AC=BD,∴OA=OC=OB=OD.∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.上内部外部上点A在⊙O内部点A在⊙O上点A在⊙O外部六、当堂检测 巩固新知(以点A为圆心,2厘米长为半径的圆)(以点A为圆心,2厘米长为半径 的圆的内部)(分别以点A 、B为圆心,2厘米长为半径的⊙ A和⊙B的交点)(分别以点A、 B为圆心,2厘米长为半径的⊙ A的内部与⊙B的内部的公共部分)思考题:BABA1、从运动和集合的观点理解圆的定义:3、证明几个点在同一个圆上的方法. 要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等.2、点与圆的位置关系:七、课堂小结 知识提升等圆、同心圆:等圆:圆心不同半径相同同心圆:圆心相同半径不同八、学习新知 理解掌握认识弧、弦、直径这些与圆有关的概念 1.弦:2.弧:如图, 弦AB,弦CD如图,直径CD圆上任意两点间的部分叫做圆弧,简称弧.连接圆上任意两点的线段叫做弦.直径:经过圆心的弦叫做直径. 半圆:圆的任意一条直径的两个端点分圆
成两 条弧,每条弧叫做半圆.认识与圆有关的概念 3.等弧:在同圆或等圆中,能够互相重合的弧
叫做等弧. 如图是某市的摩天轮的示意图. 点O是圆
心,半径r为15m,点A,B是圆上的两点,圆
心角∠AOB=120°. 你能想办法求出 的长度
吗?说说你的理由. 我们知道圆周长的计算公式为C=2πr,
其中r是圆的半径,即360°的圆心角所对
的弧长就是圆周长C.由此得出以下结论:例3 已知圆O的半径为30cm,求40°的圆心角所对的弧长(精确到0.1cm) 如图所示,一个边长为10cm的等边三角形木板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A′B′C的位置,求顶点A从开始到结束所经过的路程为多少.九、学以致用 应用新知∵ 等边三角形ABC的边长为10cm, 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形. 我们可以发现,扇形面积与组成扇形的
圆心角的大小有关,在同一个圆中,圆心角
越大,扇形面积也越大. 如何求半径为r,圆心角为n°的扇形的面积呢?由此得到:例4 如图,圆O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积.(精确0.1cm2).解 因为r=1.5cm,n=58,所以扇形OAB的面积为解 设∠AOB=n°,解得n=135°,即圆心角∠COD=135°.拓展练习连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴四边形OECD为矩形,
∠EOD=90°, OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△ODB.∴ r =12,
2.定长称为半径的长
(简称半径).
3.以点O为圆心的圆记作⊙o,读作“圆O”.圆的定义一(从运动角度):演示OA二、学习新知 理解掌握试根据圆的定义填空:
1、圆上各点到 的距离都等 于 .
2、到定点的距离等于定长的点都在 .定点(圆心)定长(半径的长)圆上定义二:圆是到定点的距离等于定长的点的集合.圆的内部:
可以看作是到圆心的距离小于半径的点的集合.
圆的外部:
可以看作是到圆心的距离大于半径的点的集合.圆的定义二(从集合角度):提问: 如果一个点到圆心距离小于半径, 那么这个点在哪里呢? 大于圆的半径呢? 反过来呢? 点与圆的位置关系点与圆的位置关系如图,设⊙O的半径为r,A点在圆内,B点在圆上,
C点在圆外,那么OA<r, OB=r, OC>r.反过来也成立,即 点的位置可以确定该点到圆心的距离与半径的关系,反过来,已知点到圆心的距离与半径的关系可以确定该点到圆的位置关系.想一想:如图所示, ⊙O是一个半径为r的圆.在圆内、圆外、圆
上分别取一点,点到圆心的距离为d,请用r与d的大小
来刻画它们的位置特征.点与圆位置关系有三种:点在圆外、点在圆上、点在圆内点在圆外,即d > r;
点在圆上,即d = r;
点在圆外,即d < r..O 车轮为什么做成圆形?三、学以致用 应用新知车轮做成三角形、正方形可以吗?如图,A,B表示车轮边缘上的两点,点O表示车轮的轴心,A,O之间的距离与B,O之间的距离有什么关系?C表示车轮边缘上的任意一点.
要使车轮能够平稳地滚动,C,
O之间的距离与A,O之间的距
离应满足什么关系?车轮边缘上任意两点到轴心的距离都相等, 任意一点到轴心的距离是一个定值.为了使投圈游戏公平,现在有一条3米长的绳子,
你准备怎么办? 四、学以致用 应用新知五、例题分析 运用新知例1 在△ABC中,∠C=900,AC=4,AB=5,以点C为圆心,以r为半径作圆,按下列条件分别判断A,B两点和⊙C的位置关系:(1) r=2.4 (2) r=4 解:∵∠C=900,AC=4,AB=5,(1) r=2.4时,∵BC=3>r ,AC=4>r ,∴A,B两点都在⊙C外.(2) r=4时,∵BC=3<r ,AC=4=r ,∴点B在⊙C内,点A在⊙C上.例2 已知四边形ABCD为矩形.试判断A,B,C,D四个点是否在同一个圆上,并说明理由.解: A,B,C,D四个点在同一个圆上.如图21-3,连接AC,BD,AC与BD相交于O.理由如下:∵四边形ABCD为矩形.又∵AC=BD,∴OA=OC=OB=OD.∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.上内部外部上点A在⊙O内部点A在⊙O上点A在⊙O外部六、当堂检测 巩固新知(以点A为圆心,2厘米长为半径的圆)(以点A为圆心,2厘米长为半径 的圆的内部)(分别以点A 、B为圆心,2厘米长为半径的⊙ A和⊙B的交点)(分别以点A、 B为圆心,2厘米长为半径的⊙ A的内部与⊙B的内部的公共部分)思考题:BABA1、从运动和集合的观点理解圆的定义:3、证明几个点在同一个圆上的方法. 要证明几个点在同一个圆上,只要证明这几个点与一个定点的距离相等.2、点与圆的位置关系:七、课堂小结 知识提升等圆、同心圆:等圆:圆心不同半径相同同心圆:圆心相同半径不同八、学习新知 理解掌握认识弧、弦、直径这些与圆有关的概念 1.弦:2.弧:如图, 弦AB,弦CD如图,直径CD圆上任意两点间的部分叫做圆弧,简称弧.连接圆上任意两点的线段叫做弦.直径:经过圆心的弦叫做直径. 半圆:圆的任意一条直径的两个端点分圆
成两 条弧,每条弧叫做半圆.认识与圆有关的概念 3.等弧:在同圆或等圆中,能够互相重合的弧
叫做等弧. 如图是某市的摩天轮的示意图. 点O是圆
心,半径r为15m,点A,B是圆上的两点,圆
心角∠AOB=120°. 你能想办法求出 的长度
吗?说说你的理由. 我们知道圆周长的计算公式为C=2πr,
其中r是圆的半径,即360°的圆心角所对
的弧长就是圆周长C.由此得出以下结论:例3 已知圆O的半径为30cm,求40°的圆心角所对的弧长(精确到0.1cm) 如图所示,一个边长为10cm的等边三角形木板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A′B′C的位置,求顶点A从开始到结束所经过的路程为多少.九、学以致用 应用新知∵ 等边三角形ABC的边长为10cm, 圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形. 我们可以发现,扇形面积与组成扇形的
圆心角的大小有关,在同一个圆中,圆心角
越大,扇形面积也越大. 如何求半径为r,圆心角为n°的扇形的面积呢?由此得到:例4 如图,圆O的半径为1.5cm,圆心角∠AOB=58°,求扇形OAB的面积.(精确0.1cm2).解 因为r=1.5cm,n=58,所以扇形OAB的面积为解 设∠AOB=n°,解得n=135°,即圆心角∠COD=135°.拓展练习连接OE、OD,∵⊙O切BC、AC于点D、E,∴OD⊥BC,OE⊥AC.∵∠C=90°,∴四边形OECD为矩形,
∠EOD=90°, OE=OD.设⊙O的半径为r,即OE=OD=r.∵∠A+∠B=90°,∠DOB+∠B=90°.∴ ∠A=∠DOB.又∵ ∠AEO=∠ODB=90°,∴△AEO∽△ODB.∴ r =12,
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
