新课标人教A版高中数学必修一3.2.2函数模型的应用实例教学课件(共20张PPT)
文档属性
| 名称 | 新课标人教A版高中数学必修一3.2.2函数模型的应用实例教学课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 10:53:31 | ||
图片预览




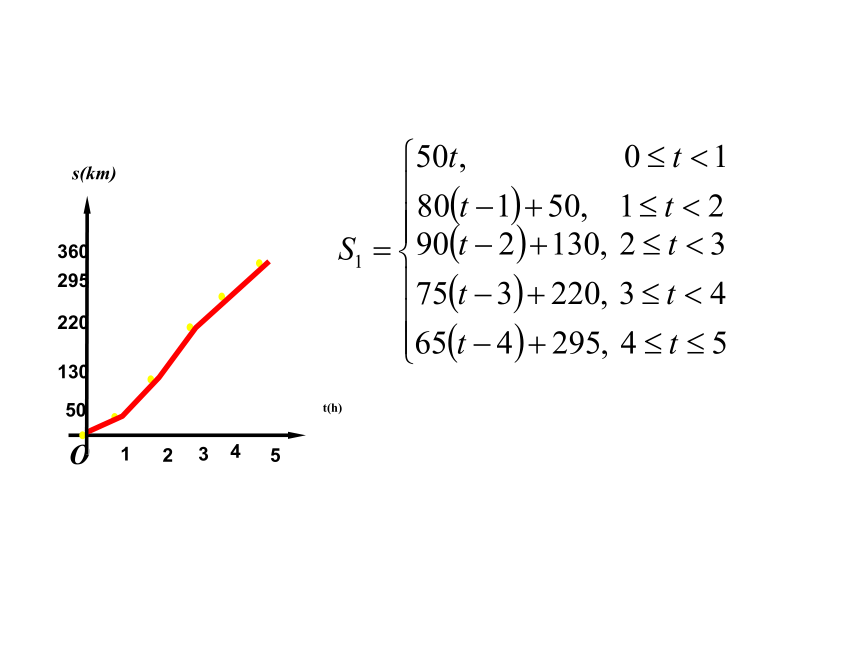

文档简介
(共20张PPT)
学习目标
1、能根据图象和表格提供的有关信息和数据,
建立确定函数模型;
2、会利用建立的函数模型解决实际问题以及会
对给出函数模型进行简单的分析和验证;
3、提升学生阅读理解、抽象概括、数据处理、
语言转换、数学建模等数学能力.
导入
1、请同学们说说我们已经学过哪些函数模型?
2、生活中函数模型的应用实例.
(3)、幂函数型
为常数,
(4)、指数函数型
为常数
(5)、对数函数型
为常数,
实例探究
类型一:根据题中信息建立函数模型
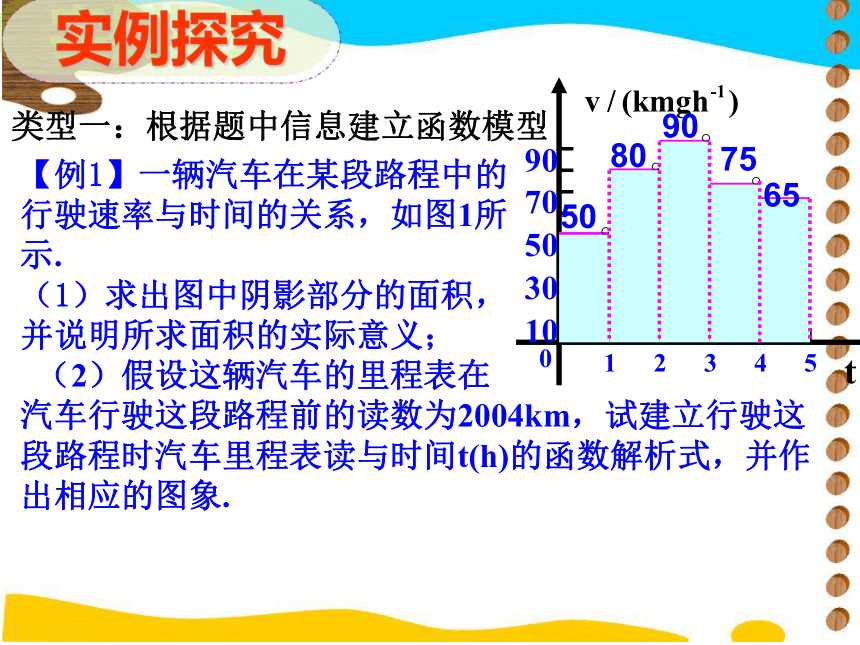
【例1】一辆汽车在某段路程中的
行驶速率与时间的关系,如图1所
示.
(1)求出图中阴影部分的面积,
并说明所求面积的实际意义;
(2)假设这辆汽车的里程表在
汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读与时间t(h)的函数解析式,并作出相应的图象.
问题1、请你根据图象写出速度关于时间变化的
函数解析式,并指出其运动规律。
问题2、试求出汽车在前2小时行驶的路程。
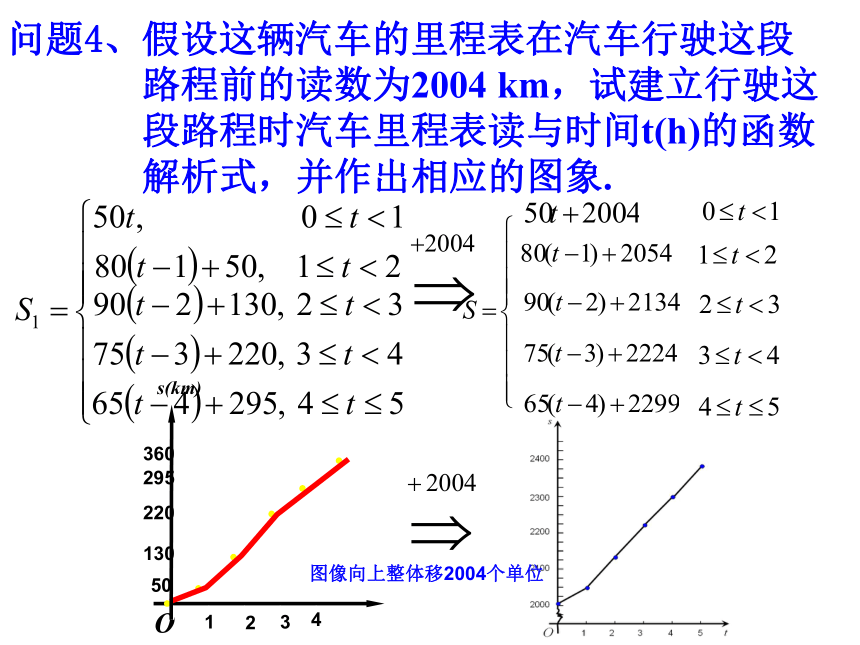
问题4、假设这辆汽车的里程表在汽车行驶这段
路程前的读数为2004 km,试建立行驶这
段路程时汽车里程表读与时间t(h)的函数
解析式,并作出相应的图象.
图像向上整体移2004个单位
问题5、分段函数是一种很重要的函数模型,在解
决分段函数问题时应注意哪几点?
问题6、通过本题的学习,你认为利用函数模型
解决实际问题应分哪几个步骤?
依据条件,分段化解
类型二:根据题中给出的函数模型,确定对应解析式,
并进一步解决实际问题
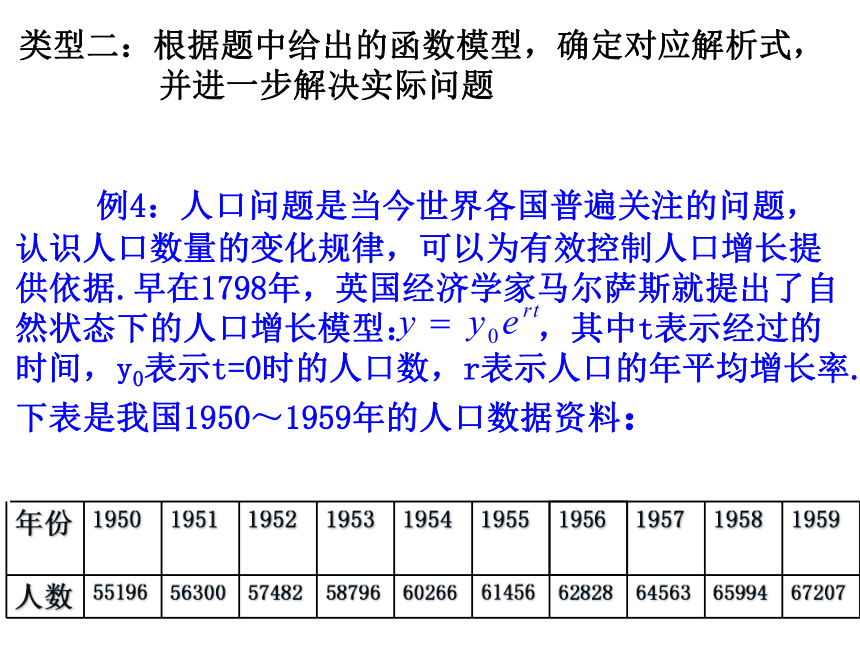
1):如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001)那么1951~1959年期间我国人口的年平均增长率是多少?
2):如果按表中的增长趋势,大约在哪一年我国的人口将达到13亿?
问题(1)、请求出1951~1959年的人口年增长率?将计算
r5式子列出来。
问题(2)、根据表中数据如何确定函数模型?
60266(1+r5)=61450
?y0表示t=0时的人口数
?如果以各年人口增长率的平均值作为
我国这一时期的人口增长率
年份 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数/万人 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
问题(3)、所得函数模型与实际人口数据是否相符?
为什么?怎样检验?为什么会与实际出现偏差?)
答:作出人口增长函数的图象,再在同一直角坐标系上根据表中数据作出散点图,观察散点是否在图象上.
根据表中数据作出散点图.
函数模型应用实例
年份 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数/万人 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
问题(4)、如何根据所确定的函数模型具体预测我国某个
时期的人口数,实质是何种计算方法?
问题(5)、按表中的增长趋势,大约在哪一年我国的人
口将达到13亿?(说出具体计算过程即可)
对于已给出模型的函数问题:
1、根据已知的部分数据,用待定系数确定函数
的解析式;
2、利用计算器或计算机作出散点图,对得到的
函数解析式进行拟合检验;
3、运用已经求出的函数模型解决相应的问题.
变式、(1)已知1650年世界人口为5亿,当时人口的年增长率为0.3%;用马尔萨斯人口模型计算,什么时候世界人口是1650年的2倍?
(2)实际上,1850年以前世界人口就超过了10亿;你对同样的模型得出的结果有何看法?(ln2
0.693)
1.客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发,经过乙地,然后到达丙地所经过的路程s与时间t之间的图像中,正确的是( )
当堂检测
2、(1)已知1970年世界人口为36亿,当时人口的年增
长率为2.1%;用马尔萨斯人口模型计算,什么时
候世界人口是1970年的2倍?
(2)实际上,而2003年世界人口还没有达到72亿。
你对同样的模型得出的结果有何看法?
(ln2 0.693)
当堂检测
【布置作业 巩固提高】
1必做题:教材P106练习第1题,P107习题3.2A组第3,4题.
2选做题:P108习题3.2B组第2题.
学习目标
1、能根据图象和表格提供的有关信息和数据,
建立确定函数模型;
2、会利用建立的函数模型解决实际问题以及会
对给出函数模型进行简单的分析和验证;
3、提升学生阅读理解、抽象概括、数据处理、
语言转换、数学建模等数学能力.
导入
1、请同学们说说我们已经学过哪些函数模型?
2、生活中函数模型的应用实例.
(3)、幂函数型
为常数,
(4)、指数函数型
为常数
(5)、对数函数型
为常数,
实例探究
类型一:根据题中信息建立函数模型
【例1】一辆汽车在某段路程中的
行驶速率与时间的关系,如图1所
示.
(1)求出图中阴影部分的面积,
并说明所求面积的实际意义;
(2)假设这辆汽车的里程表在
汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读与时间t(h)的函数解析式,并作出相应的图象.
问题1、请你根据图象写出速度关于时间变化的
函数解析式,并指出其运动规律。
问题2、试求出汽车在前2小时行驶的路程。
问题4、假设这辆汽车的里程表在汽车行驶这段
路程前的读数为2004 km,试建立行驶这
段路程时汽车里程表读与时间t(h)的函数
解析式,并作出相应的图象.
图像向上整体移2004个单位
问题5、分段函数是一种很重要的函数模型,在解
决分段函数问题时应注意哪几点?
问题6、通过本题的学习,你认为利用函数模型
解决实际问题应分哪几个步骤?
依据条件,分段化解
类型二:根据题中给出的函数模型,确定对应解析式,
并进一步解决实际问题
1):如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001)那么1951~1959年期间我国人口的年平均增长率是多少?
2):如果按表中的增长趋势,大约在哪一年我国的人口将达到13亿?
问题(1)、请求出1951~1959年的人口年增长率?将计算
r5式子列出来。
问题(2)、根据表中数据如何确定函数模型?
60266(1+r5)=61450
?y0表示t=0时的人口数
?如果以各年人口增长率的平均值作为
我国这一时期的人口增长率
年份 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数/万人 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
问题(3)、所得函数模型与实际人口数据是否相符?
为什么?怎样检验?为什么会与实际出现偏差?)
答:作出人口增长函数的图象,再在同一直角坐标系上根据表中数据作出散点图,观察散点是否在图象上.
根据表中数据作出散点图.
函数模型应用实例
年份 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959
人数/万人 55196 56300 57482 58796 60266 61456 62828 64563 65994 67207
问题(4)、如何根据所确定的函数模型具体预测我国某个
时期的人口数,实质是何种计算方法?
问题(5)、按表中的增长趋势,大约在哪一年我国的人
口将达到13亿?(说出具体计算过程即可)
对于已给出模型的函数问题:
1、根据已知的部分数据,用待定系数确定函数
的解析式;
2、利用计算器或计算机作出散点图,对得到的
函数解析式进行拟合检验;
3、运用已经求出的函数模型解决相应的问题.
变式、(1)已知1650年世界人口为5亿,当时人口的年增长率为0.3%;用马尔萨斯人口模型计算,什么时候世界人口是1650年的2倍?
(2)实际上,1850年以前世界人口就超过了10亿;你对同样的模型得出的结果有何看法?(ln2
0.693)
1.客车从甲地以60km/h的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发,经过乙地,然后到达丙地所经过的路程s与时间t之间的图像中,正确的是( )
当堂检测
2、(1)已知1970年世界人口为36亿,当时人口的年增
长率为2.1%;用马尔萨斯人口模型计算,什么时
候世界人口是1970年的2倍?
(2)实际上,而2003年世界人口还没有达到72亿。
你对同样的模型得出的结果有何看法?
(ln2 0.693)
当堂检测
【布置作业 巩固提高】
1必做题:教材P106练习第1题,P107习题3.2A组第3,4题.
2选做题:P108习题3.2B组第2题.
