人教版数学八年级上册 第15章 15.3.1 分式方程及其解法 培优训练卷(含答案)
文档属性
| 名称 | 人教版数学八年级上册 第15章 15.3.1 分式方程及其解法 培优训练卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 36.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-20 21:55:58 | ||
图片预览




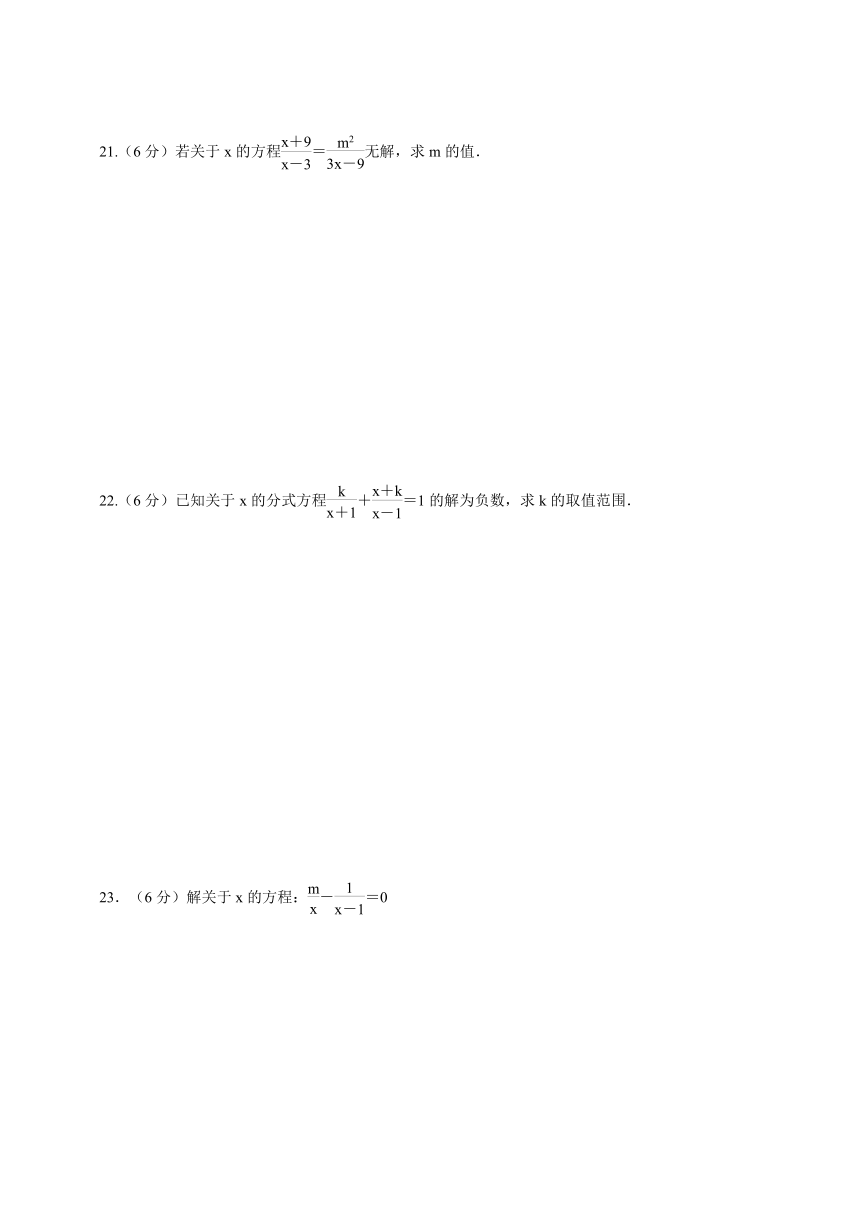
文档简介
人教版八年级上册第15章分式
15.3.1 分式方程及其解法
培优训练卷
一.选择题(共10小题,3*10=30)
1.下列方程不是分式方程的是( )
A.-x=0
B.-x=
C.+=1
D.=
2.将分式方程1-=去分母,
得到正确的整式方程是( )
A.1-2x=3
B.x-1-2x=3
C.1+2x=3
D.x-1+2x=3
3.分式方程=1的解为( )
A.x=-1 B.x=
C.x=1 D.x=2
4.把分式方程=转化为一元一次方程时,方程两边需同时乘以 ( )
A.x B.2x
C.x+4 D.x(x+4)
5. 分式方程+=1的解为( )
A.x=1 B.x=2
C.x= D.x=0
6.分式方程-1=的解是( )
A.x=1 B.x=-1±
C.x=2 D.无解
7. 对于实数a,b,定义一种新运算“?”为a?b=,这里等式右边是实数运算,例如1?3==-,则方程x?(-2)=-1的解是( )
A.x=4 B.x=5
C.x=6 D.x=7
8.若解关于x的分式方程=+时,求得的解使最简公分母为0,则这个解是( )
A.0 B.2
C.0或2 D.1
9.对于非零的两个实数a,b,规定a※b=-.若1※(x+1)=1,则x的值为( )
A. B.
C. D.-
10. 若x=3是分式方程-=0的根,则a的值是( )
A.5 B.-5
C.3 D.-3
二.填空题(共8小题,3*8=24)
11.下列方程:①=;②x-=3;③=1;④=;⑤3x+=10;⑥+=7,其中是整式方程的有 ,是分式方程的有 .(填序号)
12.(1)方程=3的解是x=____;(2)若代数式-1的值为0,则x=____.
13. x=2是分式方程-=0的根,则m= .
14.若代数式-1的值为零,则x=____.
15.已知x=1是分式方程=的根,则实数k=____.
16.当x=________时,-2与互为相反数.
17.分式方程-=0的根为 .
18.关于x的方程 =-1的解是正数,则a的取值范围是__ __.
三.解答题(共7小题,46分)
19.(6分).解下列方程:
(1)+=;
(2)=-1;
20.(6分)小明解方程-=1的过程如下.请指出他解答过程中的错误,并写出正确的解答过程.
解:方程两边同乘x,得
1-(x-2)=1……①
去括号得,1-x-2=1……②
合并同类项,得-x-1=1……③
移项,得-x=2……④
解得x=-2……⑤
∴原方程的解为x=-2……⑥
21.(6分)若关于x的方程=无解,求m的值.
22.(6分)已知关于x的分式方程+=1的解为负数,求k的取值范围.
23.(6分)解关于x的方程:-=0
24. (8分)解下列方程:
(1)+=1;
(2)+=1;
25.(8分)解方程:
①=-1的解x=__ __;
②=-1的解x=__ __;
③=-1的解x=__ __;
④=-1的解x=__ __.
(1)根据你发现的规律直接写出第⑤,⑥个方程及它们的解;
(2)请你用一个含正整数n的式子表示上述规律,并求出求解过程.
参考答案:
1-5BBADA
6-10DBCDA
11. ①④⑤,②③⑥
12. 6,3
13. 1
14. 3
15.
16.
17. x=-1
18. a>-1且a≠-
19. 解:(1)方程两边同乘以9x-3,得2(3x-1)+3x=1.
解得x=.
检验:当x=时,9x-3=0.
因此x=不是原方程的解.
∴原分式方程无解.
(2)方程两边同乘以(x-2)(x+3),得6(x+3)=x(x-2)-(x-2)(x+3).
解得x=-.
经检验,x=-是原方程的解.
20. 解:小明的解有三处错误,步骤①去分母有误:步骤②去括号有误;步骤⑥少检验.
正确的解法为:方程两边乘以x,得1-(x-2)=x,
去括号,得1-x+2=x,移项得-2x=-3,
解得x=,
经检验x=是原方程的解
21. 解:方程两边都乘3(x-3),得3(x+9)=m2,
∵方程无解,∴最简公分母3(x-3)=0,
∴x=3,
把x=3代入整式方程3(x+9)=m2,
m2=36
解得m=±6
22. 解:去分母得k(x-1)+(x+k)(x+1)=(x+1)(x-1),
整理得(2k+1)x=-1,
因为方程+=1的解为负数,
所以2k+1>0且x≠±1,即2k+1≠1且2k+1≠-1,
解得k>-且k≠0,
即k的取值范围为k>-且k≠0
23. 解:方程两边同乘以x(x-1),得m(x-1)-x=0,即(m-1)x=m.
∵m≠1,
∴x=.
检验:x=时,x(x-1)≠0.
∴原分式方程的解为x=.
24. 解:(1)去分母,得3+x(x+3)=x2-9,3+x2+3x=x2-9.
解得x=-4.
经检验,x=-4是原方程的解.
(2)方程两边乘以(x+1)(x-1),得(x+1)2+4=(x+1)(x-1),
解得x=-3,
检验:当x=-3时,(x+1)(x-1)≠0,
∴x=-3是原方程的解.
∴原方程的解是x=-3.
25. 解:①0 ②1 ③2 ④3
(1)第⑤个方程:=-1,它的解为x=4,
第⑥个方程:=-1,它的解为x=5.
(2)第n个方程:=-1,它的解为x=n-1.
方程两边都乘x+1,得n=2n-(x+1).
解得x=n-1.
