人教版九年级数学上册24.1.3 弦、弧、圆心角教学课件(共26张)
文档属性
| 名称 | 人教版九年级数学上册24.1.3 弦、弧、圆心角教学课件(共26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 11:58:19 | ||
图片预览



文档简介
(共26张PPT)
24.1.3 弧、弦、圆心角
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
2.已知点A、B都在圆上,则
(1)线段AB叫做____;
(2)圆上A、B之间的部分叫做____
1.画一个圆需要条件?
一.知识回顾
圆心
半径
弦
弧
O·
l
轴对称图形
中心对称图形
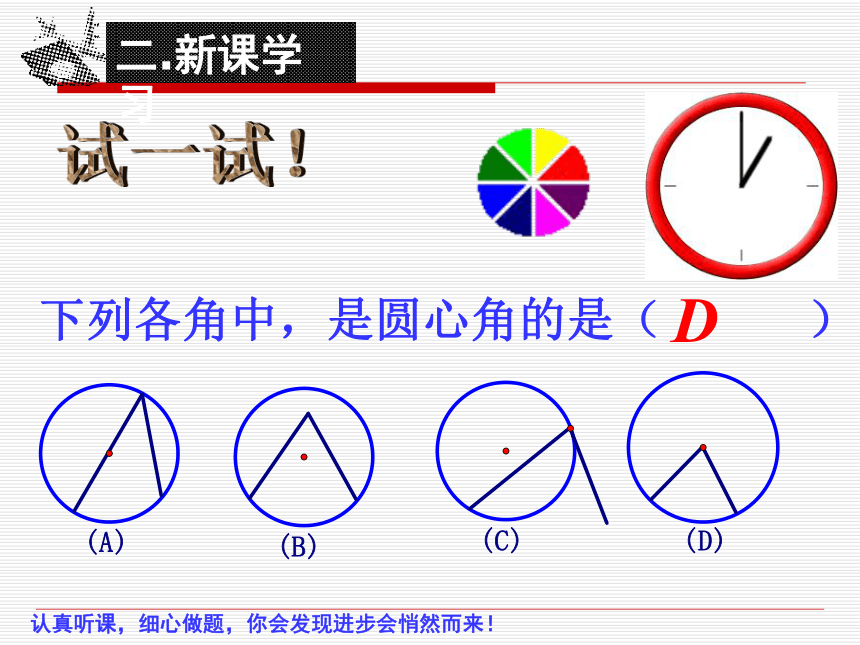
概念: 顶点在圆心上,角的两边与圆周
相交的角叫做圆心角。
二.新课学习
下列各角中,是圆心角的是( )
二.新课学习
D
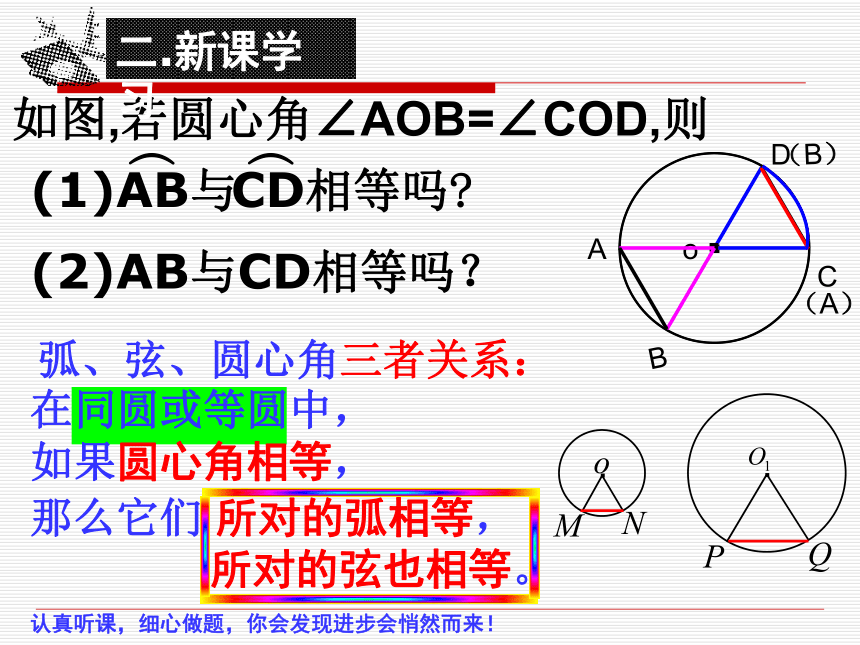
如图,若圆心角∠AOB=∠COD,则
(2)AB与CD相等吗?
弧、弦、圆心角三者关系:
在同圆或等圆中,
如果圆心角相等,
那么它们 所对的弧相等,
所对的弦也相等。
(B)
(A)
二.新课学习
·
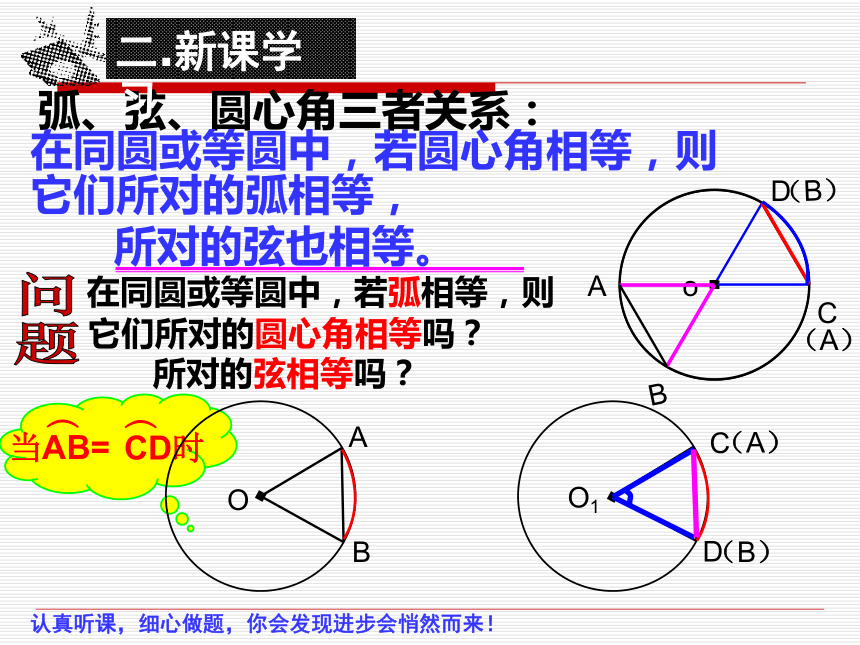
弧、弦、圆心角三者关系:
在同圆或等圆中,若圆心角相等,则
它们所对的弧相等,
所对的弦也相等。
在同圆或等圆中,若弧相等,则
它们所对的圆心角相等吗?
所对的弦相等吗?
A
B
O
(A)
(B)
(A)
(B)
二.新课学习
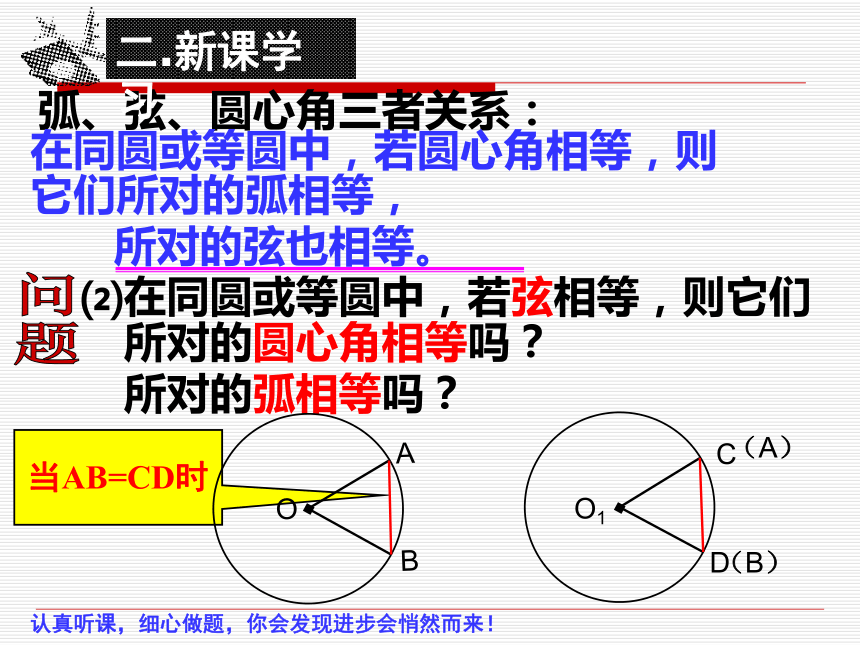
当AB=CD时
⑵在同圆或等圆中,若弦相等,则它们
所对的圆心角相等吗?
所对的弧相等吗?
B
A
O
(A)
(B)
弧、弦、圆心角三者关系:
在同圆或等圆中,若圆心角相等,则
它们所对的弧相等,
所对的弦也相等。
二.新课学习
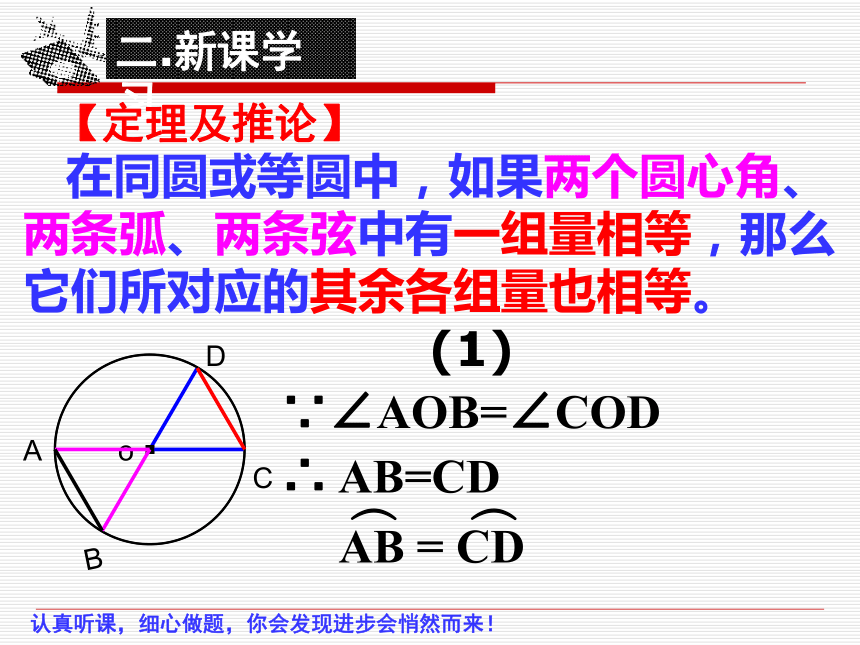
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
∵∠AOB=∠COD
(1)
∴ AB=CD
︵ ︵
AB = CD
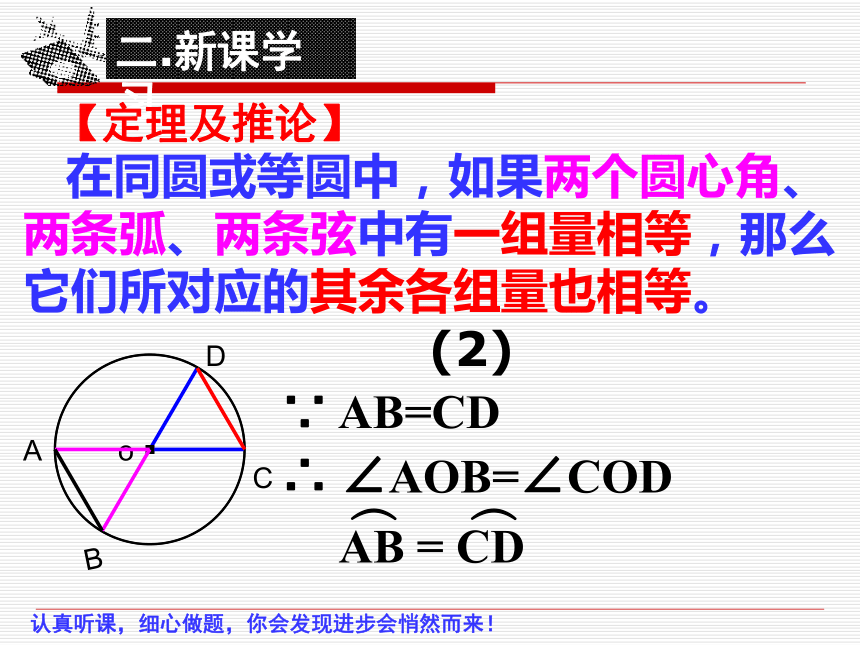
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
∵ AB=CD
(2)
∴ ∠AOB=∠COD
︵ ︵
AB = CD
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
︵ ︵
∵ AB = CD
(3)
∴ AB=CD
∠AOB=∠COD
(1)若∠AOC=∠BOC,
AC=3,则BC=____.
︵ ︵
(2)若 AC = BC,∠BOC=50°,
则∠AOC=_____.
3
三.基础练习
1.如图,已知⊙O
50°
若∠AOC=70°,则∠AOB=_____.
三.基础练习
2.如图,已知BD是⊙O的直径,
55°
︵ ︵
AB = CD
·
O
B
D
A
C
70°
证明:
∴AB=AC
又∵∠ACB=60°
∴AB=BC=CA
∴∠AOB=∠BOC=∠AOC.
·
A
B
C
O
例1:
四.典型例题
·
A
O
B
C
D
E
解:
例2:
四.典型例题
圆心角
相等
弧
相等
弦
圆心角
五.课堂小结
其余各组
也相等
(1)若∠AOC=∠BOC,BC=5,则AC=___.
(2)若 AC = BC,∠BOC=70°,
则∠AOC=_____.
5
1.如图,已知⊙O
70°
六.考题链接 相信自己一定行!
六.考题链接 相信自己一定行!
·
O
B
A
C
40°
·
D
40°
六.考题链接 相信自己一定行!
C
六.考题链接 相信自己一定行!
70°
∵
∴
AB=AC
∴
∠B=∠C =
=70°
六.考题链接 相信自己一定行!
A
O
B
C
D
·
6.如图,AB为⊙O的直径,点C、D在⊙O上,已知∠BOC=65°,AD∥OC,则(1)∠DAO=____;
(2)∠ADO=____;
(3)∠AOD=____.
65°
65°
50°
7.
六.考题链接 相信自己一定行!
B
六.备用题 努力加油!
8.
C
9.
90
六.备用题 努力加油!
10.
11.
六.备用题 努力加油!
24.1.3 弧、弦、圆心角
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
2.已知点A、B都在圆上,则
(1)线段AB叫做____;
(2)圆上A、B之间的部分叫做____
1.画一个圆需要条件?
一.知识回顾
圆心
半径
弦
弧
O·
l
轴对称图形
中心对称图形
概念: 顶点在圆心上,角的两边与圆周
相交的角叫做圆心角。
二.新课学习
下列各角中,是圆心角的是( )
二.新课学习
D
如图,若圆心角∠AOB=∠COD,则
(2)AB与CD相等吗?
弧、弦、圆心角三者关系:
在同圆或等圆中,
如果圆心角相等,
那么它们 所对的弧相等,
所对的弦也相等。
(B)
(A)
二.新课学习
·
弧、弦、圆心角三者关系:
在同圆或等圆中,若圆心角相等,则
它们所对的弧相等,
所对的弦也相等。
在同圆或等圆中,若弧相等,则
它们所对的圆心角相等吗?
所对的弦相等吗?
A
B
O
(A)
(B)
(A)
(B)
二.新课学习
当AB=CD时
⑵在同圆或等圆中,若弦相等,则它们
所对的圆心角相等吗?
所对的弧相等吗?
B
A
O
(A)
(B)
弧、弦、圆心角三者关系:
在同圆或等圆中,若圆心角相等,则
它们所对的弧相等,
所对的弦也相等。
二.新课学习
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
∵∠AOB=∠COD
(1)
∴ AB=CD
︵ ︵
AB = CD
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
∵ AB=CD
(2)
∴ ∠AOB=∠COD
︵ ︵
AB = CD
在同圆或等圆中,如果两个圆心角、
两条弧、两条弦中有一组量相等,那么
它们所对应的其余各组量也相等。
二.新课学习
【定理及推论】
︵ ︵
∵ AB = CD
(3)
∴ AB=CD
∠AOB=∠COD
(1)若∠AOC=∠BOC,
AC=3,则BC=____.
︵ ︵
(2)若 AC = BC,∠BOC=50°,
则∠AOC=_____.
3
三.基础练习
1.如图,已知⊙O
50°
若∠AOC=70°,则∠AOB=_____.
三.基础练习
2.如图,已知BD是⊙O的直径,
55°
︵ ︵
AB = CD
·
O
B
D
A
C
70°
证明:
∴AB=AC
又∵∠ACB=60°
∴AB=BC=CA
∴∠AOB=∠BOC=∠AOC.
·
A
B
C
O
例1:
四.典型例题
·
A
O
B
C
D
E
解:
例2:
四.典型例题
圆心角
相等
弧
相等
弦
圆心角
五.课堂小结
其余各组
也相等
(1)若∠AOC=∠BOC,BC=5,则AC=___.
(2)若 AC = BC,∠BOC=70°,
则∠AOC=_____.
5
1.如图,已知⊙O
70°
六.考题链接 相信自己一定行!
六.考题链接 相信自己一定行!
·
O
B
A
C
40°
·
D
40°
六.考题链接 相信自己一定行!
C
六.考题链接 相信自己一定行!
70°
∵
∴
AB=AC
∴
∠B=∠C =
=70°
六.考题链接 相信自己一定行!
A
O
B
C
D
·
6.如图,AB为⊙O的直径,点C、D在⊙O上,已知∠BOC=65°,AD∥OC,则(1)∠DAO=____;
(2)∠ADO=____;
(3)∠AOD=____.
65°
65°
50°
7.
六.考题链接 相信自己一定行!
B
六.备用题 努力加油!
8.
C
9.
90
六.备用题 努力加油!
10.
11.
六.备用题 努力加油!
同课章节目录
