人教版八年级数学下册18.1.2 平行四边形的判定(1)课件(共14张)
文档属性
| 名称 | 人教版八年级数学下册18.1.2 平行四边形的判定(1)课件(共14张) |  | |
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-11 10:18:19 | ||
图片预览





文档简介
(共14张PPT)
18.1.2 平行四边形的判定(1)
八年级下册数学
授课人:xxx 授课时间:3月14日
定
义
性
质
判
定
应
用
一、知识回顾
如图(1),已知平行四边形ABCD中,
AB=5,∠B=80°,则CD= ___,∠D=____,
∠A=_____ ,∠C=_____ .
如图(2), ABCD中,对角线AC与BD
相交于点O , AB=5,AC=6, BD=8,则
OA= ____, OB=____, AC___BD .
图(1)
图(2)
5
80°
100°
100°
3
4
⊥
一、知识回顾
3. 如图(3),已知平行四边形ABCD中,
若∠A +∠C=220°,∠A=____,∠B=___ .
4. 如图(4),四边形 ABCD是平行四边形,
周长为60,对角线 AC与BD相交于点O ,
(1)若AB=12,BD=22,则CD=____,
BC=____, OB=____;
(2)若∠ABC=70°,则∠ADC=____,
∠BCD=____.
图(3)
图(4)
110°
70°
12
18
11
70°
110°
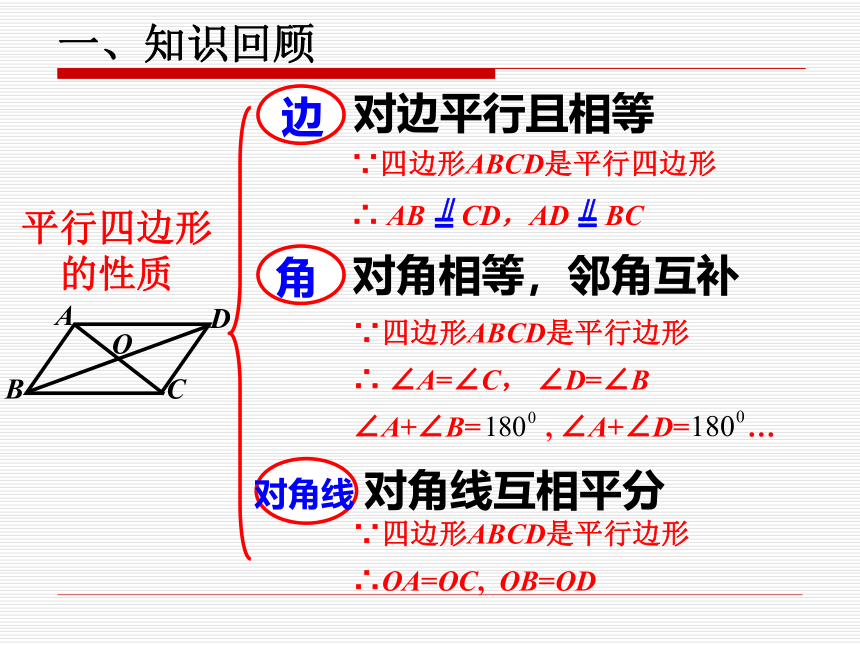
一、知识回顾
对边平行且相等
对角线互相平分
平行四边形的性质
对角相等,邻角互补
∵四边形ABCD是平行边形
∴OA=OC, OB=OD
O
二、新课学习
(一)问题引入
那么除了“两组对边分别平行”可以用来判定一个四边形是平行四边形,还有哪些方法也可以判断一个四边形是平行四边形呢?
∵ AB//CD, AD//BC
∴ 四边形ABCD是平行四边形
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
平行四边形的判定方法1:
(二)探索判别平行四边形的条件
二、新课学习
猜想1:
两组对边分别相等的四边形是平行四边形
如图,已知四边形ABCD中,__________,
__________,求证:四边形ABCD是平行四边形.
判定2:
两组对边分别平行的四边形是平行四边形
判定1:
猜想2:
两组对角分别相等的四边形是平行四边形
判定3:
AB=CD
AD=BC
猜想3:
对角线互相平分的四边形是平行四边形
∠A= ∠C
∠B= ∠D
OA=OC
OB=OD
判定4:
(1)若AD=8cm,AB=4cm,则当BC=?????? cm,
CD=?????? cm,四边形ABCD是平行四边形?.
(2)若∠A=120°,则∠B=___°,∠C=____°,
∠D=___°时,四边形ABCD是平行四边形.
8
4
60
120
60
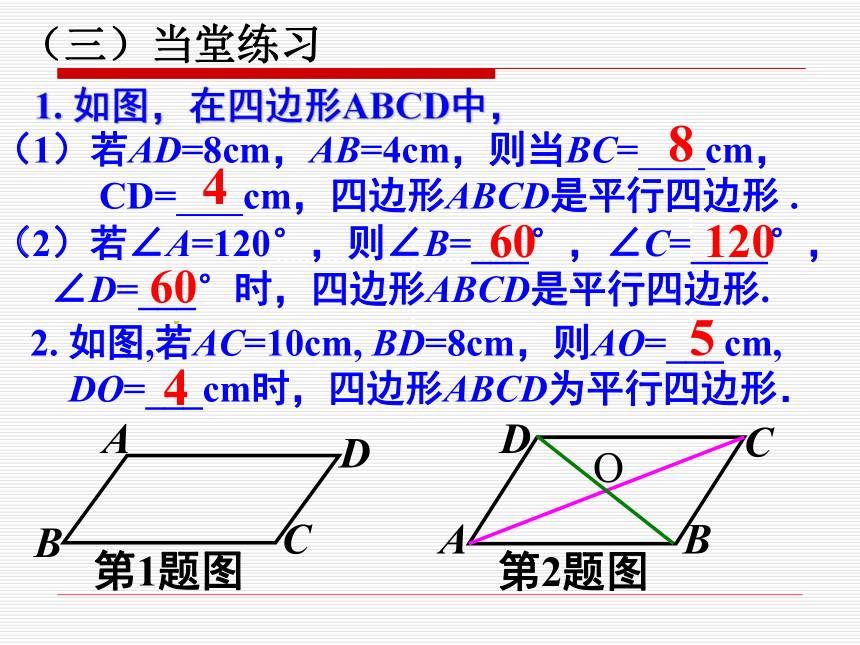
1. 如图,在四边形ABCD中,
2. 如图,若AC=10cm, BD=8cm,则AO=___cm,
DO=___cm时,四边形ABCD为平行四边形.
(三)当堂练习
5
4
第1题图
第2题图
(四)例题精讲
【例1】如图,已知 ABCD的对角线 AC 、
BD交于点O, E、F是AC上的两点,并且
AE=CF. 求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形
你还有其他方法吗?
∴ 四边形BFDE是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO -AE=CO -CF
即 EO=FO
O
连接BD交AC于点O
下列给定的条件能否判定四边形是平行四边形?
(1)AB∥CD , AD∥BC
(2)AB=CD,AD=BC
(3)∠A=∠C, ∠B=∠D
(4)AB∥CD,AD=BC
(5)AB∥CD ,∠A=∠C
(1)(2)(3)(5)
(两组对边分别平行)
(两组对边分别相等)
(两组对角分别相等)
(五)基础练习
(两组对角分别相等)
4
完成《导学案》P39
基本技能第1题(1)(2)
(五)基础练习
1
2
3
(1)
1
2
A
B
C
D
A
B
C
D
(2)
完成《导学案》P39
基本技能第1题(3)
(五)基础练习
(3)
A
B
C
D
E
F
O
如图,已知E、F分别是平行四边形ABCD 的边AD、BC的中点. 求证:BE=DF.
(六)补充练习
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决.
(1)解决一个数学问题,常要通过“动手实践”–
“ 猜想”--“验证猜想(证明)”--“得出结论”
三、课堂小结
两组对边分别相等的四边形是平行四边形
判定2:
两组对边分别平行的四边形是平行四边形
判定1:
两组对角分别相等的四边形是平行四边形
判定3:
对角线互相平分的四边形是平行四边形
判定4:
18.1.2 平行四边形的判定(1)
八年级下册数学
授课人:xxx 授课时间:3月14日
定
义
性
质
判
定
应
用
一、知识回顾
如图(1),已知平行四边形ABCD中,
AB=5,∠B=80°,则CD= ___,∠D=____,
∠A=_____ ,∠C=_____ .
如图(2), ABCD中,对角线AC与BD
相交于点O , AB=5,AC=6, BD=8,则
OA= ____, OB=____, AC___BD .
图(1)
图(2)
5
80°
100°
100°
3
4
⊥
一、知识回顾
3. 如图(3),已知平行四边形ABCD中,
若∠A +∠C=220°,∠A=____,∠B=___ .
4. 如图(4),四边形 ABCD是平行四边形,
周长为60,对角线 AC与BD相交于点O ,
(1)若AB=12,BD=22,则CD=____,
BC=____, OB=____;
(2)若∠ABC=70°,则∠ADC=____,
∠BCD=____.
图(3)
图(4)
110°
70°
12
18
11
70°
110°
一、知识回顾
对边平行且相等
对角线互相平分
平行四边形的性质
对角相等,邻角互补
∵四边形ABCD是平行边形
∴OA=OC, OB=OD
O
二、新课学习
(一)问题引入
那么除了“两组对边分别平行”可以用来判定一个四边形是平行四边形,还有哪些方法也可以判断一个四边形是平行四边形呢?
∵ AB//CD, AD//BC
∴ 四边形ABCD是平行四边形
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
平行四边形的判定方法1:
(二)探索判别平行四边形的条件
二、新课学习
猜想1:
两组对边分别相等的四边形是平行四边形
如图,已知四边形ABCD中,__________,
__________,求证:四边形ABCD是平行四边形.
判定2:
两组对边分别平行的四边形是平行四边形
判定1:
猜想2:
两组对角分别相等的四边形是平行四边形
判定3:
AB=CD
AD=BC
猜想3:
对角线互相平分的四边形是平行四边形
∠A= ∠C
∠B= ∠D
OA=OC
OB=OD
判定4:
(1)若AD=8cm,AB=4cm,则当BC=?????? cm,
CD=?????? cm,四边形ABCD是平行四边形?.
(2)若∠A=120°,则∠B=___°,∠C=____°,
∠D=___°时,四边形ABCD是平行四边形.
8
4
60
120
60
1. 如图,在四边形ABCD中,
2. 如图,若AC=10cm, BD=8cm,则AO=___cm,
DO=___cm时,四边形ABCD为平行四边形.
(三)当堂练习
5
4
第1题图
第2题图
(四)例题精讲
【例1】如图,已知 ABCD的对角线 AC 、
BD交于点O, E、F是AC上的两点,并且
AE=CF. 求证:四边形BFDE是平行四边形.
证明:∵四边形ABCD是平行四边形
你还有其他方法吗?
∴ 四边形BFDE是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO -AE=CO -CF
即 EO=FO
O
连接BD交AC于点O
下列给定的条件能否判定四边形是平行四边形?
(1)AB∥CD , AD∥BC
(2)AB=CD,AD=BC
(3)∠A=∠C, ∠B=∠D
(4)AB∥CD,AD=BC
(5)AB∥CD ,∠A=∠C
(1)(2)(3)(5)
(两组对边分别平行)
(两组对边分别相等)
(两组对角分别相等)
(五)基础练习
(两组对角分别相等)
4
完成《导学案》P39
基本技能第1题(1)(2)
(五)基础练习
1
2
3
(1)
1
2
A
B
C
D
A
B
C
D
(2)
完成《导学案》P39
基本技能第1题(3)
(五)基础练习
(3)
A
B
C
D
E
F
O
如图,已知E、F分别是平行四边形ABCD 的边AD、BC的中点. 求证:BE=DF.
(六)补充练习
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决.
(1)解决一个数学问题,常要通过“动手实践”–
“ 猜想”--“验证猜想(证明)”--“得出结论”
三、课堂小结
两组对边分别相等的四边形是平行四边形
判定2:
两组对边分别平行的四边形是平行四边形
判定1:
两组对角分别相等的四边形是平行四边形
判定3:
对角线互相平分的四边形是平行四边形
判定4:
