人教版九年级数学上册24.1.2 垂直于弦的直径(1)课件(共15张)
文档属性
| 名称 | 人教版九年级数学上册24.1.2 垂直于弦的直径(1)课件(共15张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 12:52:58 | ||
图片预览




文档简介
(共15张PPT)
24.1.2 垂直于弦的直径
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
一.知识回顾
直径
半径
⊙O
圆O
弦
轴
无数
圆心
中心
圆心
二.新课学习
1.思考下列问题:
(1)给你一个裁好的圆,你能找到这个圆
的圆心吗?
(2)沿着它的任意一条直径所在直线对折,
你会发现什么?
(3)在这个圆上尝试折出一条弦与刚才折出
的直径垂直,展开圆形纸片,再折回,
你又会发现什么?
二.新课学习
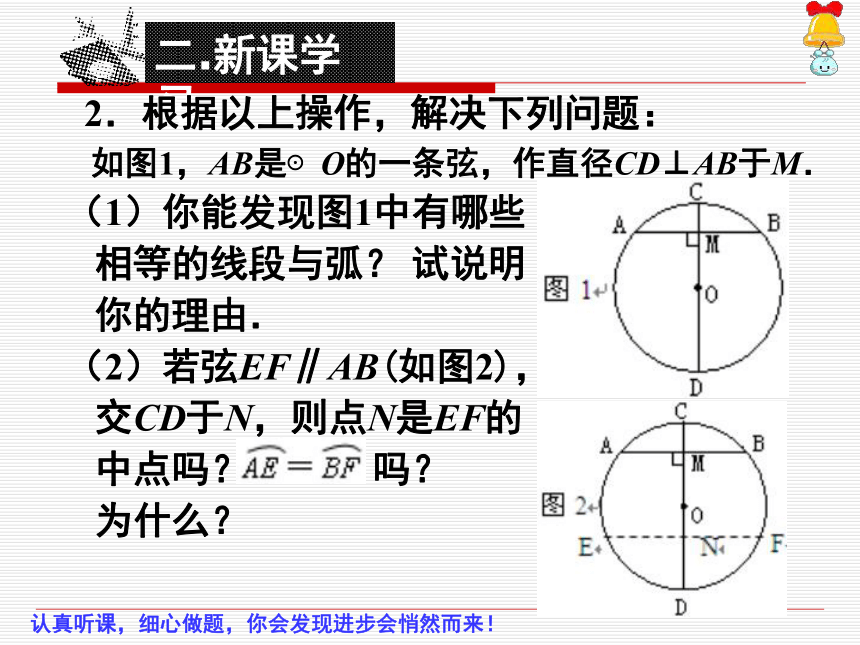
2.根据以上操作,解决下列问题:
如图1,AB是⊙O的一条弦,作直径CD⊥AB于M.
(1)你能发现图1中有哪些
相等的线段与弧? 试说明
你的理由.
(2)若弦EF∥AB(如图2),
交CD于N,则点N是EF的
中点吗? 吗?
为什么?
二.新课学习
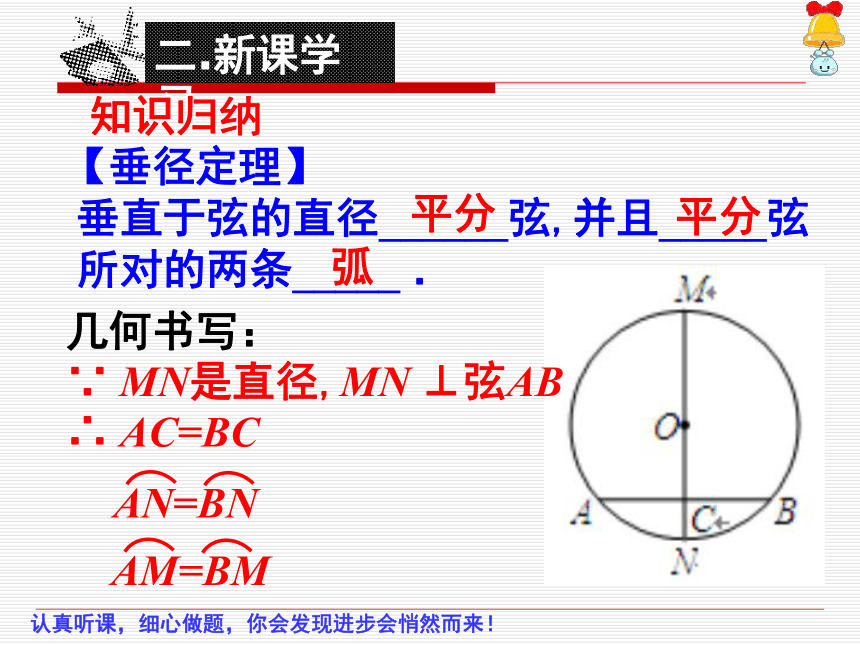
知识归纳
【垂径定理】
垂直于弦的直径______弦,并且_____弦
所对的两条_____ .
几何书写:
平分
平分
弧
∵ MN是直径,MN ⊥弦AB
∴ AC=BC
二.新课学习
知识归纳
【垂径定理】
垂直于弦的直径______弦,并且_____弦
所对的两条_____ .
平分
平分
弧
【推论1】平分弦(不是直径)的直径____
于弦,并且平分 弦所对的两条____.
垂直
弧
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
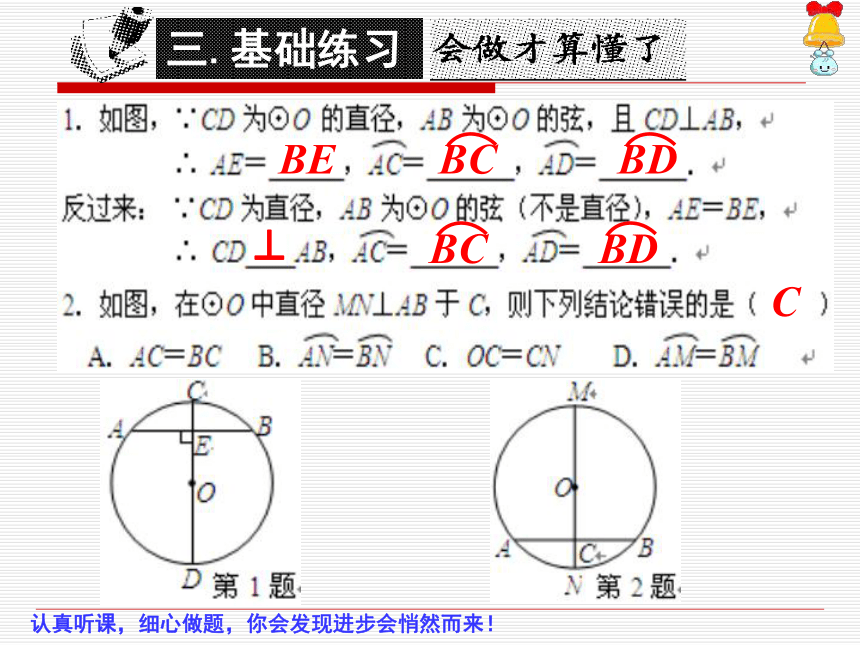
三.基础练习
BE
⊥
C
四.典型例题
解:如图,设弧AB所在的圆的
圆心为O,半径为r,过O作
OC ⊥ AB于D,交弧AB于
C,连接OA
由垂径定理得,AD=BD
∵ AB=37m,CD=7.23m
∴ AD=18.5m, OD=(r-7.23)m
在Rt△ AOD中,由勾股定理得,
(r-7.23)2+18.52=r2 解得r≈27.3m
答:赵州桥主桥拱的半径为27.3m.
五.课堂小结
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
六.考题链接 相信自己一定行!
6cm
C
解:过O作OC⊥AB于C,连接OA
依题意知OC=3cm,AB=8cm,
由垂径定理得AC=4cm
∴在Rt△AOC中,由勾股定理得
即⊙O的半径为5cm
六.考题链接 相信自己一定行!
C
解:过O作OC⊥AB于C ,连接OA
依题意知OA=12cm,AB=8cm,
由垂径定理得AC=4cm
∴在Rt△AOC中,由勾股定理得
即圆心O到AB的距离为 cm
六.考题链接 相信自己一定行!
【课后作业】
导学案P81-82
解:连接OA
∵DE=8cm,CE=2cm
∴由垂径定理得AC=4cm
∴在Rt△AOE中,由勾股定理得
∴ ⊙O直径为10cm,OA=OC=5cm
∴ OE=5-2=3cm
∵AB⊥CD
注重知识归纳;
注重基本概念;
注重典型题型;
注重每日小练;
注重错题整理;
避免盲目大意。
24.1.2 垂直于弦的直径
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
一.知识回顾
直径
半径
⊙O
圆O
弦
轴
无数
圆心
中心
圆心
二.新课学习
1.思考下列问题:
(1)给你一个裁好的圆,你能找到这个圆
的圆心吗?
(2)沿着它的任意一条直径所在直线对折,
你会发现什么?
(3)在这个圆上尝试折出一条弦与刚才折出
的直径垂直,展开圆形纸片,再折回,
你又会发现什么?
二.新课学习
2.根据以上操作,解决下列问题:
如图1,AB是⊙O的一条弦,作直径CD⊥AB于M.
(1)你能发现图1中有哪些
相等的线段与弧? 试说明
你的理由.
(2)若弦EF∥AB(如图2),
交CD于N,则点N是EF的
中点吗? 吗?
为什么?
二.新课学习
知识归纳
【垂径定理】
垂直于弦的直径______弦,并且_____弦
所对的两条_____ .
几何书写:
平分
平分
弧
∵ MN是直径,MN ⊥弦AB
∴ AC=BC
二.新课学习
知识归纳
【垂径定理】
垂直于弦的直径______弦,并且_____弦
所对的两条_____ .
平分
平分
弧
【推论1】平分弦(不是直径)的直径____
于弦,并且平分 弦所对的两条____.
垂直
弧
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
三.基础练习
BE
⊥
C
四.典型例题
解:如图,设弧AB所在的圆的
圆心为O,半径为r,过O作
OC ⊥ AB于D,交弧AB于
C,连接OA
由垂径定理得,AD=BD
∵ AB=37m,CD=7.23m
∴ AD=18.5m, OD=(r-7.23)m
在Rt△ AOD中,由勾股定理得,
(r-7.23)2+18.52=r2 解得r≈27.3m
答:赵州桥主桥拱的半径为27.3m.
五.课堂小结
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
六.考题链接 相信自己一定行!
6cm
C
解:过O作OC⊥AB于C,连接OA
依题意知OC=3cm,AB=8cm,
由垂径定理得AC=4cm
∴在Rt△AOC中,由勾股定理得
即⊙O的半径为5cm
六.考题链接 相信自己一定行!
C
解:过O作OC⊥AB于C ,连接OA
依题意知OA=12cm,AB=8cm,
由垂径定理得AC=4cm
∴在Rt△AOC中,由勾股定理得
即圆心O到AB的距离为 cm
六.考题链接 相信自己一定行!
【课后作业】
导学案P81-82
解:连接OA
∵DE=8cm,CE=2cm
∴由垂径定理得AC=4cm
∴在Rt△AOE中,由勾股定理得
∴ ⊙O直径为10cm,OA=OC=5cm
∴ OE=5-2=3cm
∵AB⊥CD
注重知识归纳;
注重基本概念;
注重典型题型;
注重每日小练;
注重错题整理;
避免盲目大意。
同课章节目录
