人教版九年级数学上册24.1.2 垂直于弦的直径(2)课件(共14张)
文档属性
| 名称 | 人教版九年级数学上册24.1.2 垂直于弦的直径(2)课件(共14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 964.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 13:13:23 | ||
图片预览




文档简介
(共14张PPT)
24.1.2 垂直于弦的直径(2)
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
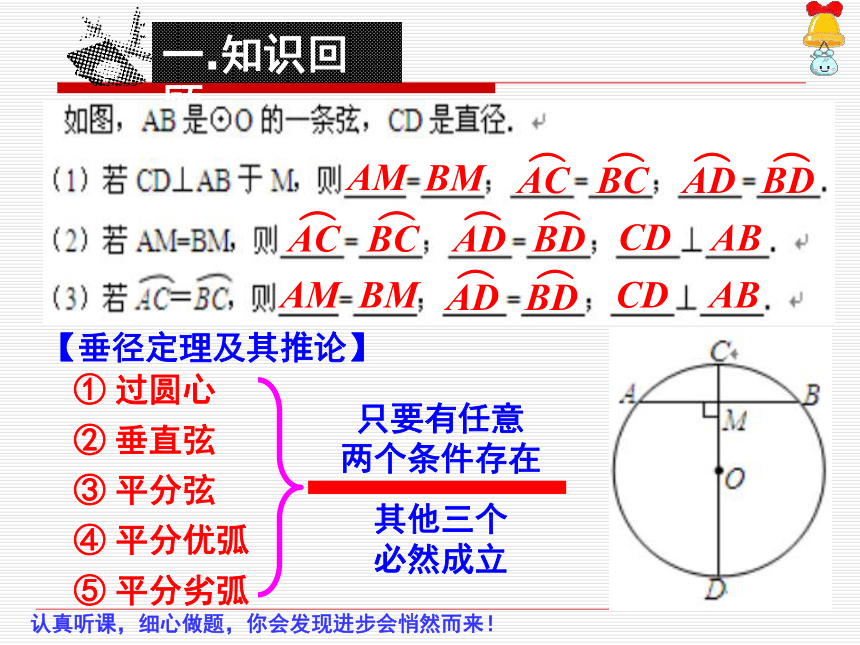
一.知识回顾
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
AM
BM
︵
AC
︵
BC
︵
AD
︵
BD
︵
AC
︵
BC
︵
AD
︵
BD
CD
AB
AM
BM
︵
AD
︵
BD
CD
AB
二.新课学习
E
F
若弦EF∥AB
N
(1)点N是EF的中点吗?
(2) 吗?
【垂径定理推论2】
两条平行弦所夹的弧_______.
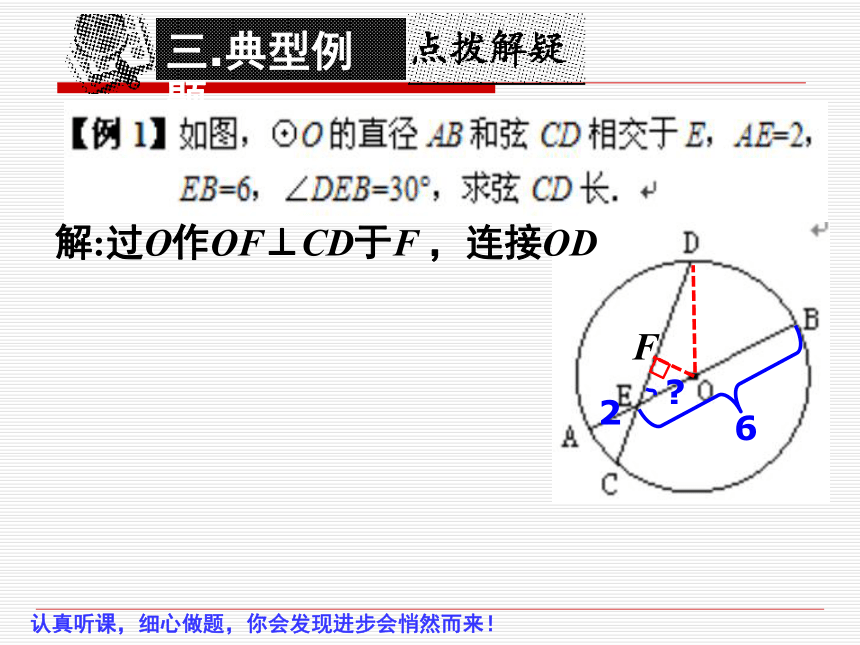
三.典型例题
F
解:过O作OF⊥CD于F ,连接OD
2
6
?
三.典型例题
四.基础练习
四.基础练习
四.基础练习
五.考题链接 相信自己一定行!
五.考题链接 相信自己一定行!
五.课堂小结
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
【课后作业】作业本P38
注重知识归纳;
注重基本概念;
注重典型题型;
注重每日小练;
注重错题整理;
避免盲目大意。
自主预习,检测预习效果
(一)学习目标
1.了解解直角三角形的含义
2.掌握直角三角形中各元素之间的关系,并会利
用这些关系解直角三角形.
如图,AB是(O的一条弦,CD是直径.
(1)若CD⊥AB于M,则
(2)若AM=BM,则
(3)若AC=BC,则
⊥
少典對图典例析,名师感解疑
★已知两边解直角三角形
例1如图1,在Rt△ABC中,∠C=90°,AC=V2
BC=√6,解这个直角三角形.
分析:已知两条直角边AC和BC,由勾般定理可
求出斜边AB的长,再根据正切求∠A和∠B即可
四阶梯训练主练兵,会做才算懂了
A组:基础练习
1.李东沿着坡度为1:2的山坡向上走了1000m,
他升高了
A.200V5m
B.500m
C.500V3m
D.1000m
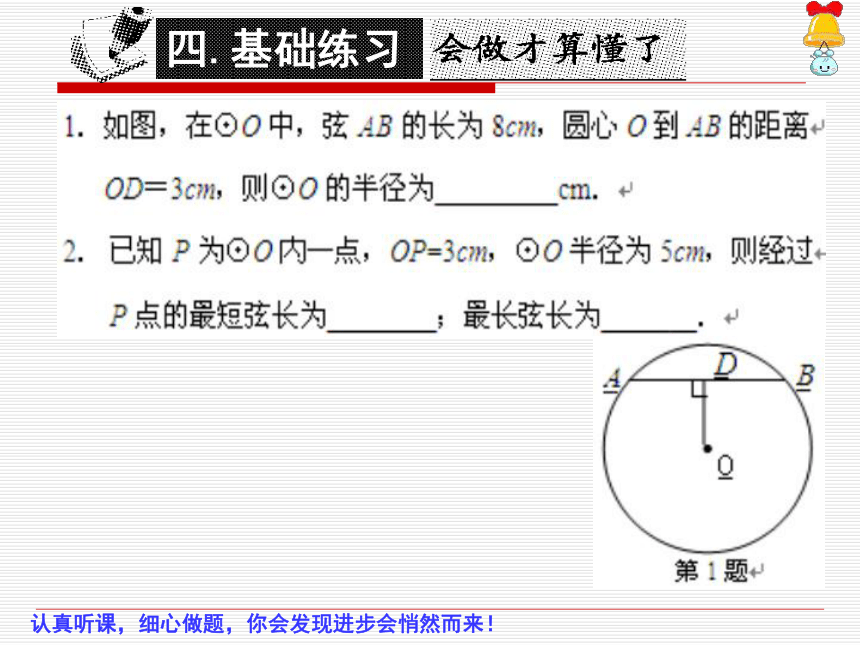
如图,在⊙0中,弦AB的长为8cm,圆心O到AB的距离
OD=3cm,则⊙0的半径为
cm。
2.已知P为⊙O内一点,OP=3cm,⊙0半径为5cm,则经过
P点的最短弦长为
最长弦长为
G1五考题链跳战经典课后自主演练
7(2011年清远市)如图10,小明以3m/s的速
度从山脚A点爬到山顶页B点,已知点B到山脚的垂
直距离BC为24m,且山坡坡角∠A的度数为28°,问
小明从山脚爬上山顶需要多长时间(结果精确到0.1,
参考数据:sin28°≈0.47,cos28°≈0.88,tan28
053)?
24.1.2 垂直于弦的直径(2)
一、知识回顾
二、新课学习
三、基础练习
四、典型例题
五、课堂小结
六、考题链接
一.知识回顾
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
AM
BM
︵
AC
︵
BC
︵
AD
︵
BD
︵
AC
︵
BC
︵
AD
︵
BD
CD
AB
AM
BM
︵
AD
︵
BD
CD
AB
二.新课学习
E
F
若弦EF∥AB
N
(1)点N是EF的中点吗?
(2) 吗?
【垂径定理推论2】
两条平行弦所夹的弧_______.
三.典型例题
F
解:过O作OF⊥CD于F ,连接OD
2
6
?
三.典型例题
四.基础练习
四.基础练习
四.基础练习
五.考题链接 相信自己一定行!
五.考题链接 相信自己一定行!
五.课堂小结
① 过圆心
② 垂直弦
③ 平分弦
④ 平分优弧
⑤ 平分劣弧
只要有任意
两个条件存在
其他三个
必然成立
【垂径定理及其推论】
【课后作业】作业本P38
注重知识归纳;
注重基本概念;
注重典型题型;
注重每日小练;
注重错题整理;
避免盲目大意。
自主预习,检测预习效果
(一)学习目标
1.了解解直角三角形的含义
2.掌握直角三角形中各元素之间的关系,并会利
用这些关系解直角三角形.
如图,AB是(O的一条弦,CD是直径.
(1)若CD⊥AB于M,则
(2)若AM=BM,则
(3)若AC=BC,则
⊥
少典對图典例析,名师感解疑
★已知两边解直角三角形
例1如图1,在Rt△ABC中,∠C=90°,AC=V2
BC=√6,解这个直角三角形.
分析:已知两条直角边AC和BC,由勾般定理可
求出斜边AB的长,再根据正切求∠A和∠B即可
四阶梯训练主练兵,会做才算懂了
A组:基础练习
1.李东沿着坡度为1:2的山坡向上走了1000m,
他升高了
A.200V5m
B.500m
C.500V3m
D.1000m
如图,在⊙0中,弦AB的长为8cm,圆心O到AB的距离
OD=3cm,则⊙0的半径为
cm。
2.已知P为⊙O内一点,OP=3cm,⊙0半径为5cm,则经过
P点的最短弦长为
最长弦长为
G1五考题链跳战经典课后自主演练
7(2011年清远市)如图10,小明以3m/s的速
度从山脚A点爬到山顶页B点,已知点B到山脚的垂
直距离BC为24m,且山坡坡角∠A的度数为28°,问
小明从山脚爬上山顶需要多长时间(结果精确到0.1,
参考数据:sin28°≈0.47,cos28°≈0.88,tan28
053)?
同课章节目录
