人教版高中数学必修一第二章 2.2.2对数函数及其性质(共20张PPT)
文档属性
| 名称 | 人教版高中数学必修一第二章 2.2.2对数函数及其性质(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 12:27:17 | ||
图片预览





文档简介
(共20张PPT)
*
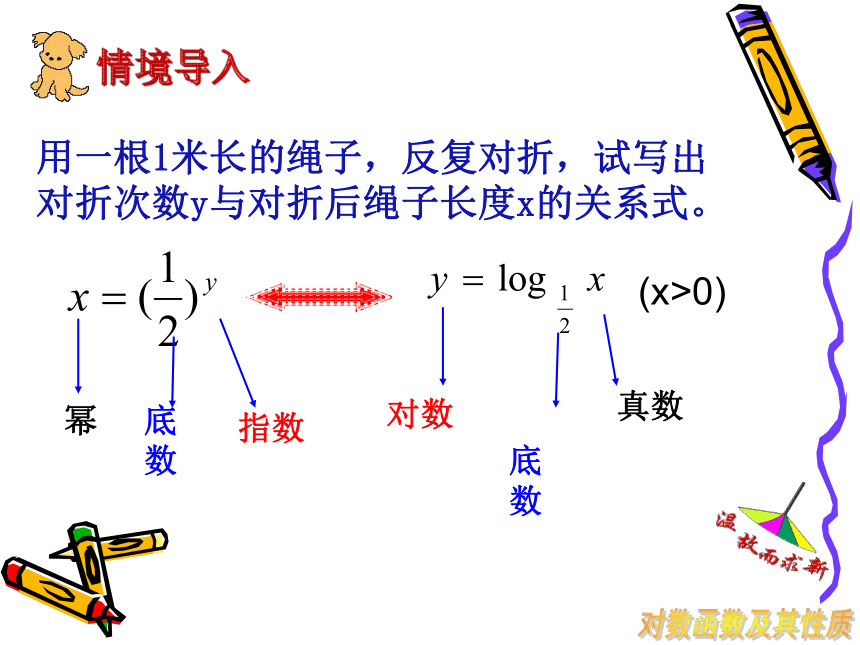
用一根1米长的绳子,反复对折,试写出对折次数y与对折后绳子长度x的关系式。
?系数为1;?底数是大于0,且不等于1的常数; ?对数的真数仅有自变量x.
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
定义:函数
1、判断:以下函数是对数函数的( )
(1)y=log2(3x-2) (2) y=log(x-1)x
(3)y=log1/3x2 (3)y=lnx
(5)
4和6
的图象和性质:
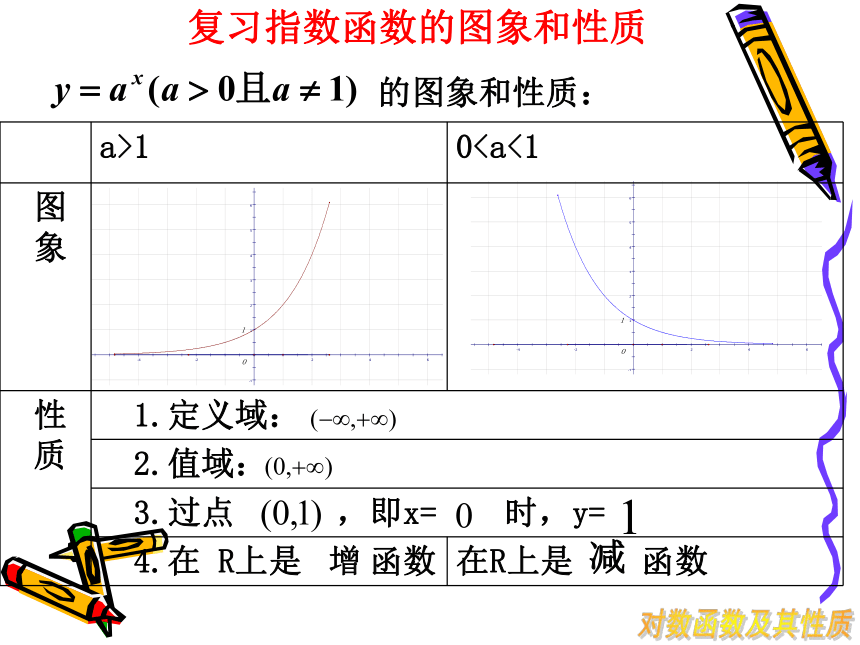
复习指数函数的图象和性质
a>1 0图
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
试试:同一坐标系中画出下列对数函数的图象
1、
2、
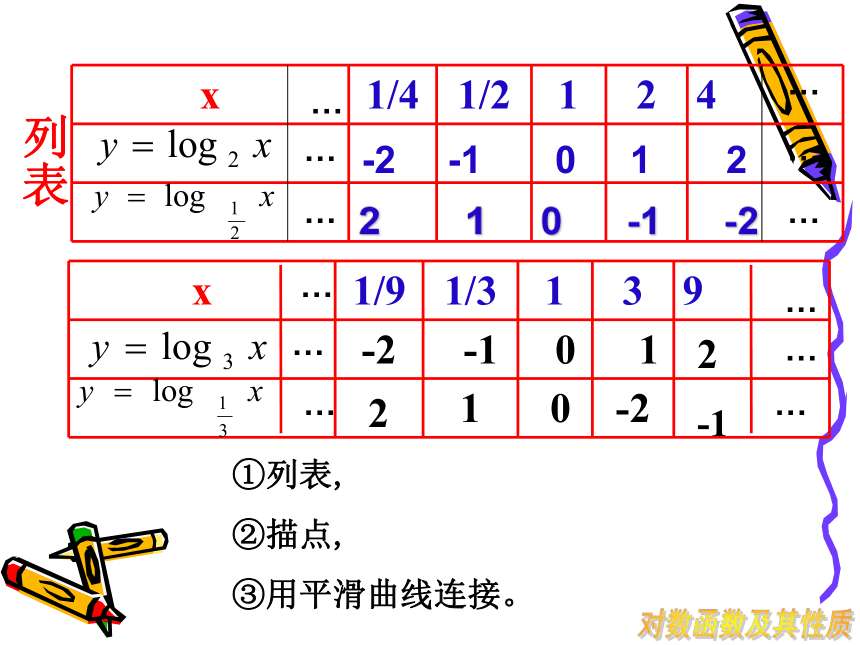
列表
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
…
…
…
…
…
…
2
2
-1
①列表,
②描点,
③用平滑曲线连接。
x 1/4 1/2 1 2 4
x 1/9 1/3 1 3 9
-2 -1 0 1
1 0 -2
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
y=log3x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
y
图象特征 代数表述
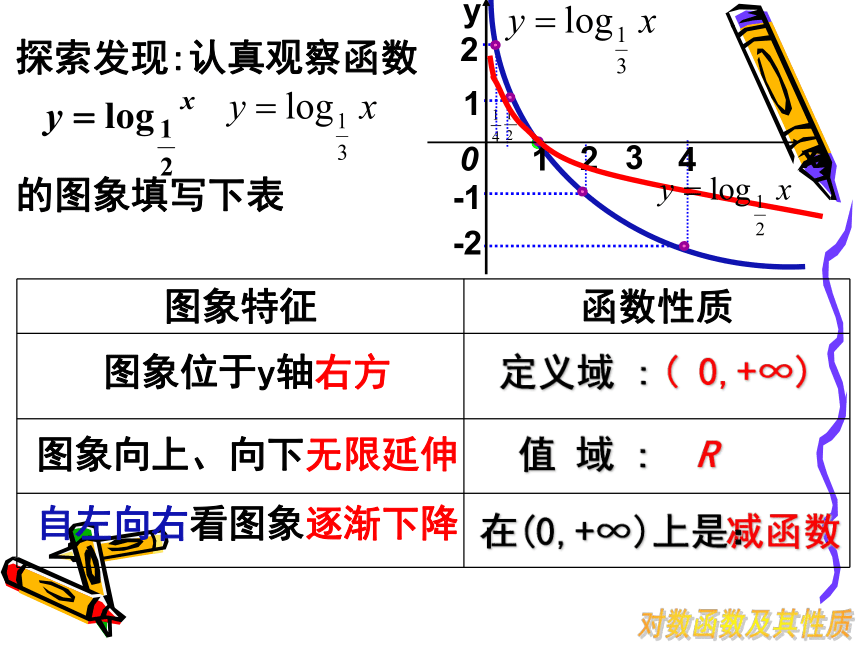
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探索发现:认真观察函数
的图象填写下表
图象特征 函数性质
观察“几何画板课件”
归纳对数函数 (a>0,且a≠1)的图像及性质
对数函数y=log a x (a>0, a≠1)
(4) 0 x>1时, y>0
(4) 00;
x>1时, y<0
(3) 过点(1,0), 即x=1 时, y=0
(1) 定义域: (0,+∞)
(2) 值域:R
x
y
o
(1, 0)
x
y
o
(1, 0)
(5)在(0,+∞)上是减函数
(5) 在(0,+∞)上是增函数
图
象
a>1 0
性
质
O
X
Y
1
Y=logdx
b>a>d>c
规律:在第一象限内,从顺时针方向看,
底数越大,图像越靠近x轴。
探究底数变化图象的变化
探索研究:
这两组函数的图象有什么关系呢?
底数互为倒数的两个对数函数图像关于x轴对称
例1 、
求下列函数的定义域:(a >0 且a≠1 )
(1) y=logax2
(2) y=loga(4-x)
解∶(1)
x2>0
x≠0
∴函数定义域是
∴函数y=loga(4-x)的定义域是{x│ x<4 }
{x│x≠0 }
∴函数y=log (x-1)(x+2)的定义域是
{x│x>1且x ≠ 2 }
(×)
(√)
(×)
( 1 ,0 )
(×)
(1) 类比记忆指数函数和对数函数。
(2)看见函数式想图像,结合图像记性质。
作业:课本? P73.练习2.?P75,10组2题
(2)看见函数式想图像,结合图像记性质。
(1) 类比记忆指数函数和对数函数。
类比指数函数的单调性比较大小:
(1)
(2)
和
和
*
用一根1米长的绳子,反复对折,试写出对折次数y与对折后绳子长度x的关系式。
?系数为1;?底数是大于0,且不等于1的常数; ?对数的真数仅有自变量x.
,且
叫做对数函数,其中x是自变量,函数的定义域是(0,+∞)。
定义:函数
1、判断:以下函数是对数函数的( )
(1)y=log2(3x-2) (2) y=log(x-1)x
(3)y=log1/3x2 (3)y=lnx
(5)
4和6
的图象和性质:
复习指数函数的图象和性质
a>1 0
象
性
质 1.定义域:
2.值域:
3.过点 ,即x= 时,y=
4.在 R上是 函数 在R上是 函数
试试:同一坐标系中画出下列对数函数的图象
1、
2、
列表
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
…
…
…
…
…
…
2
2
-1
①列表,
②描点,
③用平滑曲线连接。
x 1/4 1/2 1 2 4
x 1/9 1/3 1 3 9
-2 -1 0 1
1 0 -2
定义域 :
( 0,+∞)
值 域 :
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
y=log3x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
y
图象特征 代数表述
定义域 :
( 0,+∞)
值 域 :
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探索发现:认真观察函数
的图象填写下表
图象特征 函数性质
观察“几何画板课件”
归纳对数函数 (a>0,且a≠1)的图像及性质
对数函数y=log a x (a>0, a≠1)
(4) 0
(4) 0
x>1时, y<0
(3) 过点(1,0), 即x=1 时, y=0
(1) 定义域: (0,+∞)
(2) 值域:R
x
y
o
(1, 0)
x
y
o
(1, 0)
(5)在(0,+∞)上是减函数
(5) 在(0,+∞)上是增函数
图
象
a>1 0
性
质
O
X
Y
1
Y=logdx
b>a>d>c
规律:在第一象限内,从顺时针方向看,
底数越大,图像越靠近x轴。
探究底数变化图象的变化
探索研究:
这两组函数的图象有什么关系呢?
底数互为倒数的两个对数函数图像关于x轴对称
例1 、
求下列函数的定义域:(a >0 且a≠1 )
(1) y=logax2
(2) y=loga(4-x)
解∶(1)
x2>0
x≠0
∴函数定义域是
∴函数y=loga(4-x)的定义域是{x│ x<4 }
{x│x≠0 }
∴函数y=log (x-1)(x+2)的定义域是
{x│x>1且x ≠ 2 }
(×)
(√)
(×)
( 1 ,0 )
(×)
(1) 类比记忆指数函数和对数函数。
(2)看见函数式想图像,结合图像记性质。
作业:课本? P73.练习2.?P75,10组2题
(2)看见函数式想图像,结合图像记性质。
(1) 类比记忆指数函数和对数函数。
类比指数函数的单调性比较大小:
(1)
(2)
和
和
