2019-2020学年河北省秦皇岛市海港区八年级(上)期中数学试卷(解析版)
文档属性
| 名称 | 2019-2020学年河北省秦皇岛市海港区八年级(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 07:22:54 | ||
图片预览



文档简介
2019-2020学年河北省秦皇岛市海港区八年级(上)
期中数学试卷
一、选择题(每题2分,共20分)
1.,,,,中,分式的个数有
A.2个 B.3个 C.4个 D.5个
2.在实数,3.14159,,,,,中,无理数的个数是
A.1 B.2 C.3 D.4
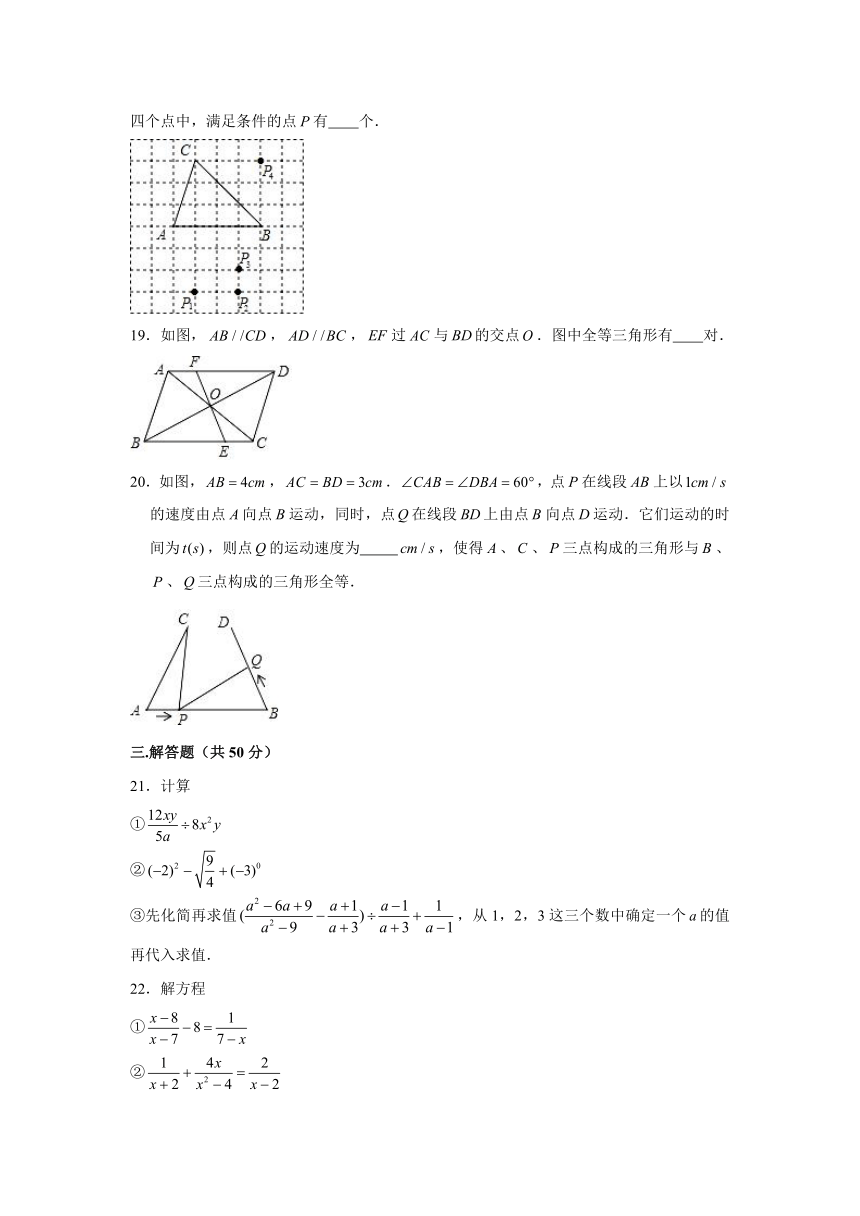
3.下列计算不正确的一项是
A. B.
C. D.
4.一个立方体的体积是,它的棱长大约在
A.与之间 B.与之间 C.与之间 D.与之间
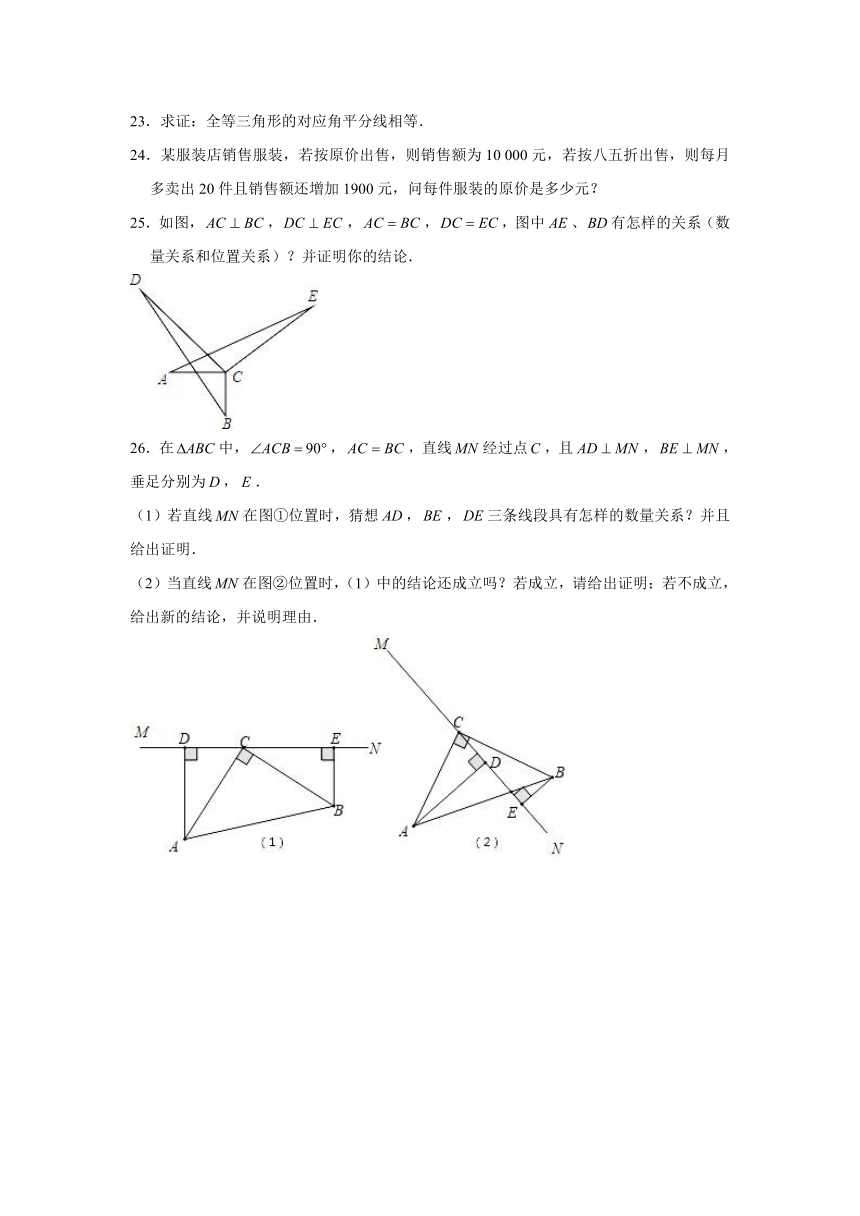
5.用直尺和圆规作一个角等于已知角,如图,能得出的依据是
A. B. C. D.
6.已知、两地相距40千米,、两地相距50千米,甲乙两车分别从、两地同时出发到地.若乙车每小时比甲车多行驶12千米,则两车同时到达地.设乙车的速度为千米小时,依题意列方程正确的是
A. B. C. D.
7.在下列条件中,能判定和△全等的是
A.,, B.,,
C.,, D.,,.
8.如图所示,于点,且,,若,则
A. B. C. D.
9.下列几种说法正确的有
①无理数都是无限小数;②带根号的数是无理数;
③实数分为正实数和负实数;④无理数包括正无理数、0和负无理数.
A.①②③④ B.②③ C.①④ D.①
10.如图,在与中,,,,,,三点在一条直线上,连接,.有以下结论:①;②;③;其中正确的个数有
A.0 B.1 C.2 D.3
二.填空题(每题3分,共30分)
11.的平方根是 ,的立方根是 .
12.分式,,的最简公分母是 .
13.计算 .
14.有意义,则满足的条件是 .
15.有一个数值转换器,原理如下图所示,当输入的值为16时,输出的值是 .
16.已知的平方根是,的算术平方根是4,则的平方根是 .
17.若分式方程有增根,则的值是 .
18.如图,在方格纸中,以为一边作,使之与全等,从,,,,四个点中,满足条件的点有 个.
19.如图,,,过与的交点.图中全等三角形有 对.
20.如图,,.,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为,则点的运动速度为 ,使得、、三点构成的三角形与、、三点构成的三角形全等.
三.解答题(共50分)
21.计算
①
②
③先化简再求值,从1,2,3这三个数中确定一个的值再代入求值.
22.解方程
①
②
23.求证:全等三角形的对应角平分线相等.
24.某服装店销售服装,若按原价出售,则销售额为10 000元,若按八五折出售,则每月多卖出20件且销售额还增加1900元,问每件服装的原价是多少元?
25.如图,,,,,图中、有怎样的关系(数量关系和位置关系)?并证明你的结论.
26.在中,,,直线经过点,且,,垂足分别为,.
(1)若直线在图①位置时,猜想,,三条线段具有怎样的数量关系?并且给出证明.
(2)当直线在图②位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,给出新的结论,并说明理由.
2019-2020学年河北省秦皇岛市海港区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题2分,共20分)
1.,,,,中,分式的个数有
A.2个 B.3个 C.4个 D.5个
【解答】解:这一组式子中,,中分母含有未知数,故是分式.
故选:.
2.在实数,3.14159,,,,,中,无理数的个数是
A.1 B.2 C.3 D.4
【解答】解:3.14159是有限小数,属于有理数;,是整数,属于有理数;是分数,属于有理数;是循环小数,属于有理数.
无理数有:,,共3个.
故选:.
3.下列计算不正确的一项是
A. B.
C. D.
【解答】解:、当时,原式,错误;
、原式,正确;
、原式,正确;
、原式,正确,
故选:.
4.一个立方体的体积是,它的棱长大约在
A.与之间 B.与之间 C.与之间 D.与之间
【解答】解:棱长为:,
,
,
即它的棱长大约在与之间.
故选:.
5.用直尺和圆规作一个角等于已知角,如图,能得出的依据是
A. B. C. D.
【解答】解:作图的步骤:
①以为圆心,任意长为半径画弧,分别交、于点、;
②任意作一点,作射线,以为圆心,长为半径画弧,交于点;
③以为圆心,长为半径画弧,交前弧于点;
④过点作射线.
所以就是与相等的角;
作图完毕.
在与△,
,
△,
,
显然运用的判定方法是.
故选:.
6.已知、两地相距40千米,、两地相距50千米,甲乙两车分别从、两地同时出发到地.若乙车每小时比甲车多行驶12千米,则两车同时到达地.设乙车的速度为千米小时,依题意列方程正确的是
A. B. C. D.
【解答】解:设乙车的速度为千米小时,则甲车的速度为千米小时,
由题意得,.
故选:.
7.在下列条件中,能判定和△全等的是
A.,, B.,,
C.,, D.,,.
【解答】解:当,,时,不能判定和△全等,与不是已知两边的夹角;
当,,时,不能判定和△全等,不是与的夹边;
当,,时,不能判定和△全等,不存在的方法;
当,,时,能判定和△全等,依据是.
故选:.
8.如图所示,于点,且,,若,则
A. B. C. D.
【解答】解:在和,
,,
,
,
又,
.
在和中,
,,,
,
.
.
所以,本题应选择.
9.下列几种说法正确的有
①无理数都是无限小数;②带根号的数是无理数;
③实数分为正实数和负实数;④无理数包括正无理数、0和负无理数.
A.①②③④ B.②③ C.①④ D.①
【解答】解:(1)无理数都是无限小数,故说法正确;
(2)带根号的开方开不尽的数才是无理数,故说法错误;
(3)实数分为正实数和负实数,还有0,故说法错误;
(4)无理数包括正无理数和负无理数,0是有理数,故说法错误.
故选:.
10.如图,在与中,,,,,,三点在一条直线上,连接,.有以下结论:①;②;③;其中正确的个数有
A.0 B.1 C.2 D.3
【解答】解:,
,即,
在和中,,
,
,③正确;
为等腰直角三角形,
,
,
,
,
,②正确;
,
,
,
则,①正确;
正确的有3个,
故选:.
二.填空题(每题3分,共30分)
11.的平方根是 ,的立方根是 .
【解答】解:因为,所以的平方根是;
的立方根是.
故答案为:,.
12.分式,,的最简公分母是 .
【解答】解:分式,,的最简公分母是;
故答案为:.
13.计算 .
【解答】解:原式
故答案为:
14.有意义,则满足的条件是 .
【解答】解:有意义,则,
解得:.
故答案为:.
15.有一个数值转换器,原理如下图所示,当输入的值为16时,输出的值是 .
【解答】解:的算术平方根式4,4是有理数,
又的算术平方根式2,2是有理数,
还需求2的算术平方根是,
是无理数,
的值是.
故答案为:.
16.已知的平方根是,的算术平方根是4,则的平方根是 .
【解答】解:的平方根为,
,
解得,
的算术平方根为4,
,
解得,
,
的平方根为.
故答案为:.
17.若分式方程有增根,则的值是 .
【解答】解:去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:,
解得:,
故答案为:.
18.如图,在方格纸中,以为一边作,使之与全等,从,,,,四个点中,满足条件的点有 2 个.
【解答】解:有和,共2个,
理由是:设小正方形的边长为1,
当点时,根据勾股定理得:,,
,根据即可推出;
当点时,根据勾股定理得:,,
,根据即可推出
故答案为:2.
19.如图,,,过与的交点.图中全等三角形有 6 对.
【解答】解:图中全等三角形有:,,,,,,共6对,
理由是:,,
,,,
在和中
,
同理;
,,
根据可以推出,,
,,
根据可以推出,,
故答案为:6.
20.如图,,.,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为,则点的运动速度为 1或1.5 ,使得、、三点构成的三角形与、、三点构成的三角形全等.
【解答】解:设点的运动速度是,
,
、、三点构成的三角形与、、三点构成的三角形全等,有两种情况:
①,,
则,
解得:,
则,
解得:;
②,,
则,,
解得:,,
故答案为:1或1.5.
三.解答题(共50分)
21.计算
①
②
③先化简再求值,从1,2,3这三个数中确定一个的值再代入求值.
【解答】解:①原式;
②原式;
③原式
,
当或1时无意义,故,
则原式.
22.解方程
①
②
【解答】解:①去分母得:,
解得:,
经检验是增根,分式方程无解;
②去分母得:,
解得:,
经检验是增根,分式方程无解.
23.求证:全等三角形的对应角平分线相等.
【解答】已知:如图,△,、是和的平分线,
求证:,
证明:△,
,,
,
平分,平分,
,
△,
.
24.某服装店销售服装,若按原价出售,则销售额为10 000元,若按八五折出售,则每月多卖出20件且销售额还增加1900元,问每件服装的原价是多少元?
【解答】解:设每件服装的原价是元.
则:.
解之得:.
经检验:是原方程的解.
答:每件服装的原价是200元.
25.如图,,,,,图中、有怎样的关系(数量关系和位置关系)?并证明你的结论.
【解答】解:结论:,,
理由:如图,设交于,交于,
,,
,
在和中,
,
,
,
,
,
,
.
26.在中,,,直线经过点,且,,垂足分别为,.
(1)若直线在图①位置时,猜想,,三条线段具有怎样的数量关系?并且给出证明.
(2)当直线在图②位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,给出新的结论,并说明理由.
【解答】解:(1)猜想,
证明:,,
,
,
,
在和中,
,
,,
,
;
(2)答:(1)中的结论不成立,理由如下:
同理可证得,
,,
,
.
期中数学试卷
一、选择题(每题2分,共20分)
1.,,,,中,分式的个数有
A.2个 B.3个 C.4个 D.5个
2.在实数,3.14159,,,,,中,无理数的个数是
A.1 B.2 C.3 D.4
3.下列计算不正确的一项是
A. B.
C. D.
4.一个立方体的体积是,它的棱长大约在
A.与之间 B.与之间 C.与之间 D.与之间
5.用直尺和圆规作一个角等于已知角,如图,能得出的依据是
A. B. C. D.
6.已知、两地相距40千米,、两地相距50千米,甲乙两车分别从、两地同时出发到地.若乙车每小时比甲车多行驶12千米,则两车同时到达地.设乙车的速度为千米小时,依题意列方程正确的是
A. B. C. D.
7.在下列条件中,能判定和△全等的是
A.,, B.,,
C.,, D.,,.
8.如图所示,于点,且,,若,则
A. B. C. D.
9.下列几种说法正确的有
①无理数都是无限小数;②带根号的数是无理数;
③实数分为正实数和负实数;④无理数包括正无理数、0和负无理数.
A.①②③④ B.②③ C.①④ D.①
10.如图,在与中,,,,,,三点在一条直线上,连接,.有以下结论:①;②;③;其中正确的个数有
A.0 B.1 C.2 D.3
二.填空题(每题3分,共30分)
11.的平方根是 ,的立方根是 .
12.分式,,的最简公分母是 .
13.计算 .
14.有意义,则满足的条件是 .
15.有一个数值转换器,原理如下图所示,当输入的值为16时,输出的值是 .
16.已知的平方根是,的算术平方根是4,则的平方根是 .
17.若分式方程有增根,则的值是 .
18.如图,在方格纸中,以为一边作,使之与全等,从,,,,四个点中,满足条件的点有 个.
19.如图,,,过与的交点.图中全等三角形有 对.
20.如图,,.,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为,则点的运动速度为 ,使得、、三点构成的三角形与、、三点构成的三角形全等.
三.解答题(共50分)
21.计算
①
②
③先化简再求值,从1,2,3这三个数中确定一个的值再代入求值.
22.解方程
①
②
23.求证:全等三角形的对应角平分线相等.
24.某服装店销售服装,若按原价出售,则销售额为10 000元,若按八五折出售,则每月多卖出20件且销售额还增加1900元,问每件服装的原价是多少元?
25.如图,,,,,图中、有怎样的关系(数量关系和位置关系)?并证明你的结论.
26.在中,,,直线经过点,且,,垂足分别为,.
(1)若直线在图①位置时,猜想,,三条线段具有怎样的数量关系?并且给出证明.
(2)当直线在图②位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,给出新的结论,并说明理由.
2019-2020学年河北省秦皇岛市海港区八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(每题2分,共20分)
1.,,,,中,分式的个数有
A.2个 B.3个 C.4个 D.5个
【解答】解:这一组式子中,,中分母含有未知数,故是分式.
故选:.
2.在实数,3.14159,,,,,中,无理数的个数是
A.1 B.2 C.3 D.4
【解答】解:3.14159是有限小数,属于有理数;,是整数,属于有理数;是分数,属于有理数;是循环小数,属于有理数.
无理数有:,,共3个.
故选:.
3.下列计算不正确的一项是
A. B.
C. D.
【解答】解:、当时,原式,错误;
、原式,正确;
、原式,正确;
、原式,正确,
故选:.
4.一个立方体的体积是,它的棱长大约在
A.与之间 B.与之间 C.与之间 D.与之间
【解答】解:棱长为:,
,
,
即它的棱长大约在与之间.
故选:.
5.用直尺和圆规作一个角等于已知角,如图,能得出的依据是
A. B. C. D.
【解答】解:作图的步骤:
①以为圆心,任意长为半径画弧,分别交、于点、;
②任意作一点,作射线,以为圆心,长为半径画弧,交于点;
③以为圆心,长为半径画弧,交前弧于点;
④过点作射线.
所以就是与相等的角;
作图完毕.
在与△,
,
△,
,
显然运用的判定方法是.
故选:.
6.已知、两地相距40千米,、两地相距50千米,甲乙两车分别从、两地同时出发到地.若乙车每小时比甲车多行驶12千米,则两车同时到达地.设乙车的速度为千米小时,依题意列方程正确的是
A. B. C. D.
【解答】解:设乙车的速度为千米小时,则甲车的速度为千米小时,
由题意得,.
故选:.
7.在下列条件中,能判定和△全等的是
A.,, B.,,
C.,, D.,,.
【解答】解:当,,时,不能判定和△全等,与不是已知两边的夹角;
当,,时,不能判定和△全等,不是与的夹边;
当,,时,不能判定和△全等,不存在的方法;
当,,时,能判定和△全等,依据是.
故选:.
8.如图所示,于点,且,,若,则
A. B. C. D.
【解答】解:在和,
,,
,
,
又,
.
在和中,
,,,
,
.
.
所以,本题应选择.
9.下列几种说法正确的有
①无理数都是无限小数;②带根号的数是无理数;
③实数分为正实数和负实数;④无理数包括正无理数、0和负无理数.
A.①②③④ B.②③ C.①④ D.①
【解答】解:(1)无理数都是无限小数,故说法正确;
(2)带根号的开方开不尽的数才是无理数,故说法错误;
(3)实数分为正实数和负实数,还有0,故说法错误;
(4)无理数包括正无理数和负无理数,0是有理数,故说法错误.
故选:.
10.如图,在与中,,,,,,三点在一条直线上,连接,.有以下结论:①;②;③;其中正确的个数有
A.0 B.1 C.2 D.3
【解答】解:,
,即,
在和中,,
,
,③正确;
为等腰直角三角形,
,
,
,
,
,②正确;
,
,
,
则,①正确;
正确的有3个,
故选:.
二.填空题(每题3分,共30分)
11.的平方根是 ,的立方根是 .
【解答】解:因为,所以的平方根是;
的立方根是.
故答案为:,.
12.分式,,的最简公分母是 .
【解答】解:分式,,的最简公分母是;
故答案为:.
13.计算 .
【解答】解:原式
故答案为:
14.有意义,则满足的条件是 .
【解答】解:有意义,则,
解得:.
故答案为:.
15.有一个数值转换器,原理如下图所示,当输入的值为16时,输出的值是 .
【解答】解:的算术平方根式4,4是有理数,
又的算术平方根式2,2是有理数,
还需求2的算术平方根是,
是无理数,
的值是.
故答案为:.
16.已知的平方根是,的算术平方根是4,则的平方根是 .
【解答】解:的平方根为,
,
解得,
的算术平方根为4,
,
解得,
,
的平方根为.
故答案为:.
17.若分式方程有增根,则的值是 .
【解答】解:去分母得:,
由分式方程有增根,得到,即,
把代入整式方程得:,
解得:,
故答案为:.
18.如图,在方格纸中,以为一边作,使之与全等,从,,,,四个点中,满足条件的点有 2 个.
【解答】解:有和,共2个,
理由是:设小正方形的边长为1,
当点时,根据勾股定理得:,,
,根据即可推出;
当点时,根据勾股定理得:,,
,根据即可推出
故答案为:2.
19.如图,,,过与的交点.图中全等三角形有 6 对.
【解答】解:图中全等三角形有:,,,,,,共6对,
理由是:,,
,,,
在和中
,
同理;
,,
根据可以推出,,
,,
根据可以推出,,
故答案为:6.
20.如图,,.,点在线段上以的速度由点向点运动,同时,点在线段上由点向点运动.它们运动的时间为,则点的运动速度为 1或1.5 ,使得、、三点构成的三角形与、、三点构成的三角形全等.
【解答】解:设点的运动速度是,
,
、、三点构成的三角形与、、三点构成的三角形全等,有两种情况:
①,,
则,
解得:,
则,
解得:;
②,,
则,,
解得:,,
故答案为:1或1.5.
三.解答题(共50分)
21.计算
①
②
③先化简再求值,从1,2,3这三个数中确定一个的值再代入求值.
【解答】解:①原式;
②原式;
③原式
,
当或1时无意义,故,
则原式.
22.解方程
①
②
【解答】解:①去分母得:,
解得:,
经检验是增根,分式方程无解;
②去分母得:,
解得:,
经检验是增根,分式方程无解.
23.求证:全等三角形的对应角平分线相等.
【解答】已知:如图,△,、是和的平分线,
求证:,
证明:△,
,,
,
平分,平分,
,
△,
.
24.某服装店销售服装,若按原价出售,则销售额为10 000元,若按八五折出售,则每月多卖出20件且销售额还增加1900元,问每件服装的原价是多少元?
【解答】解:设每件服装的原价是元.
则:.
解之得:.
经检验:是原方程的解.
答:每件服装的原价是200元.
25.如图,,,,,图中、有怎样的关系(数量关系和位置关系)?并证明你的结论.
【解答】解:结论:,,
理由:如图,设交于,交于,
,,
,
在和中,
,
,
,
,
,
,
.
26.在中,,,直线经过点,且,,垂足分别为,.
(1)若直线在图①位置时,猜想,,三条线段具有怎样的数量关系?并且给出证明.
(2)当直线在图②位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,给出新的结论,并说明理由.
【解答】解:(1)猜想,
证明:,,
,
,
,
在和中,
,
,,
,
;
(2)答:(1)中的结论不成立,理由如下:
同理可证得,
,,
,
.
同课章节目录
