2019-2020学年黑龙江省哈尔滨市尚志市八年级(上)期中数学试卷(五四学制)(解析版)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市尚志市八年级(上)期中数学试卷(五四学制)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览

文档简介
2019-2020学年黑龙江省哈尔滨市尚志市八年级(上)期中数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.下列图形中,不是轴对称图形的是
A. B.
C. D.
2.一个多边形的外角和与它的内角和相等,则多边形是
A.三角形 B.四边形 C.五边形 D.六边形
3.点关于轴对称的点的坐标是
A . B . C . D .
4.等腰三角形的顶角是,则它的底角是
A. B. C.或 D.或
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
6.到三角形三条边的距离都相等的点是这个三角形的
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
7.一个三角形三个内角的度数比为,这个三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
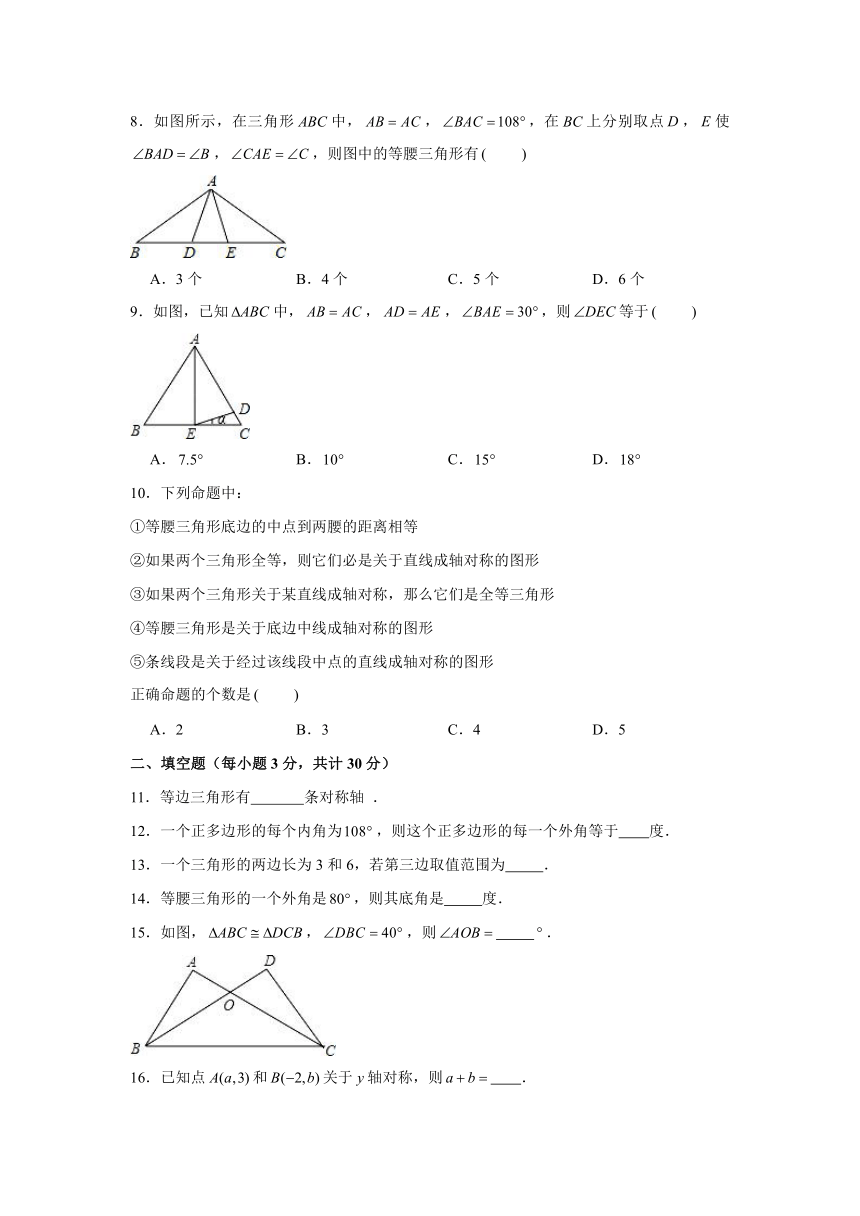
8.如图所示,在三角形中,,,在上分别取点,使,,则图中的等腰三角形有
A.3个 B.4个 C.5个 D.6个
9.如图,已知中,,,,则等于
A. B. C. D.
10.下列命题中:
①等腰三角形底边的中点到两腰的距离相等
②如果两个三角形全等,则它们必是关于直线成轴对称的图形
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形
④等腰三角形是关于底边中线成轴对称的图形
⑤条线段是关于经过该线段中点的直线成轴对称的图形
正确命题的个数是
A.2 B.3 C.4 D.5
二、填空题(每小题3分,共计30分)
11.等边三角形有 条对称轴 .
12.一个正多边形的每个内角为,则这个正多边形的每一个外角等于 度.
13.一个三角形的两边长为3和6,若第三边取值范围为 .
14.等腰三角形的一个外角是,则其底角是 度.
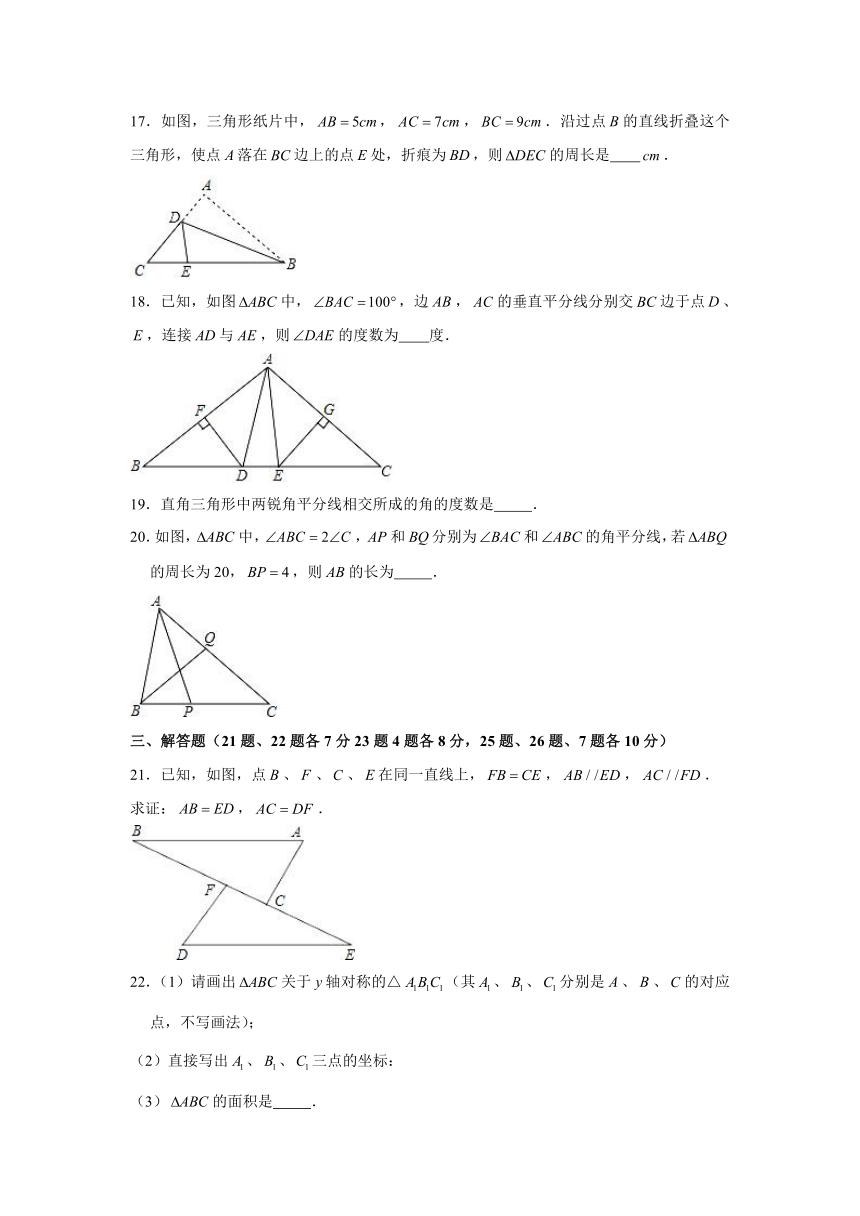
15.如图,,,则 .
16.已知点和关于轴对称,则 .
17.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 .
18.已知,如图中,,边,的垂直平分线分别交边于点、,连接与,则的度数为 度.
19.直角三角形中两锐角平分线相交所成的角的度数是 .
20.如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 .
三、解答题(21题、22题各7分23题4题各8分,25题、26题、7题各10分)
21.已知,如图,点、、、在同一直线上,,,.
求证:,.
22.(1)请画出关于轴对称的△(其、、分别是、、的对应点,不写画法);
(2)直接写出、、三点的坐标:
(3)的面积是 .
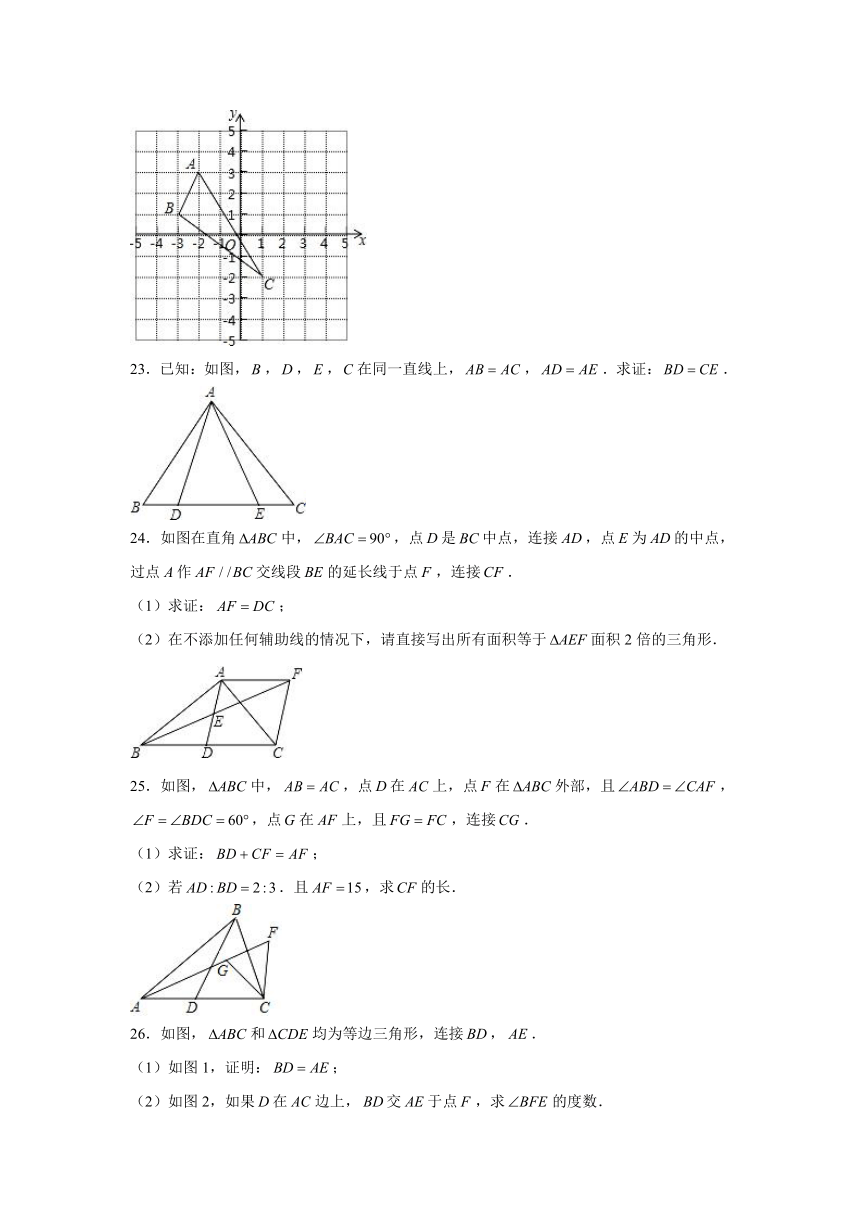
23.已知:如图,,,,在同一直线上,,.求证:.
24.如图在直角中,,点是中点,连接,点为的中点,过点作交线段的延长线于点,连接.
(1)求证:;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于面积2倍的三角形.
25.如图,中,,点在上,点在外部,且,,点在上,且,连接.
(1)求证:;
(2)若.且,求的长.
26.如图,和均为等边三角形,连接,.
(1)如图1,证明:;
(2)如图2,如果在边上,交于点,求的度数.
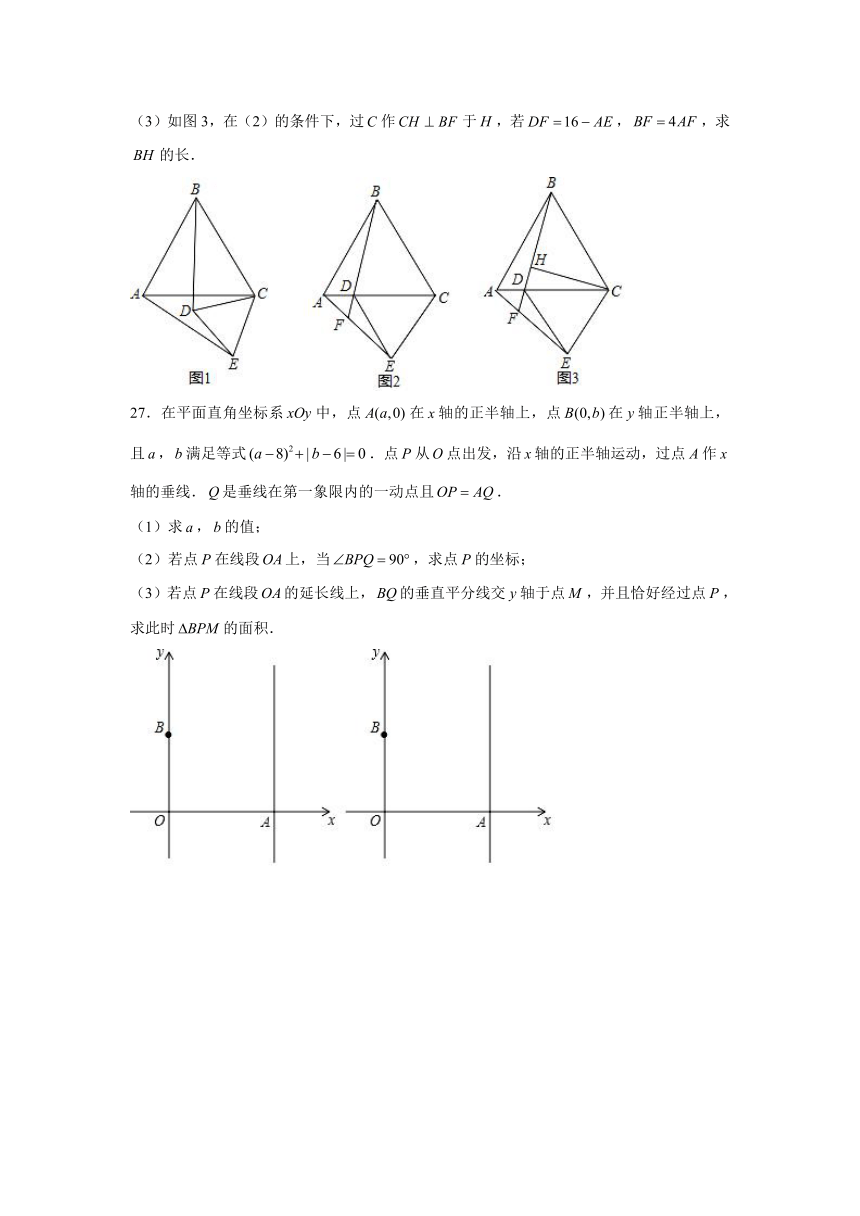
(3)如图3,在(2)的条件下,过作于,若,,求的长.
27.在平面直角坐标系中,点在轴的正半轴上,点在轴正半轴上,且,满足等式.点从点出发,沿轴的正半轴运动,过点作轴的垂线.是垂线在第一象限内的一动点且.
(1)求,的值;
(2)若点在线段上,当,求点的坐标;
(3)若点在线段的延长线上,的垂直平分线交轴于点,并且恰好经过点,求此时的面积.
2019-2020学年黑龙江省哈尔滨市尚志市八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.下列图形中,不是轴对称图形的是
A. B.
C. D.
【解答】解:、不是轴对称图形,故此选项符合题意;
、是轴对称图形,故此选项不合题意;
、是轴对称图形,故此选项不合题意;
、是轴对称图形,故此选项不合题意;
故选:.
2.一个多边形的外角和与它的内角和相等,则多边形是
A.三角形 B.四边形 C.五边形 D.六边形
【解答】解:设多边形的边数为.
根据题意得:,
解得:.
故选:.
3.点关于轴对称的点的坐标是
A . B . C . D .
【解答】解:关于轴对称的点, 横坐标相同, 纵坐标互为相反数,
点关于轴对称的点的坐标是.
故选:.
4.等腰三角形的顶角是,则它的底角是
A. B. C.或 D.或
【解答】解:因为等腰三角形的两个底角相等,
又因为顶角是,
所以其底角为.
故选:.
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
【解答】解:、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故选项错误;
、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故选项错误;
、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合判定,故选项正确;
、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故选项错误.
故选:.
6.到三角形三条边的距离都相等的点是这个三角形的
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
【解答】解:
角的平分线上的点到角的两边的距离相等,
到三角形的三边的距离相等的点是三条角平分线的交点.
故选:.
7.一个三角形三个内角的度数比为,这个三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
【解答】解:一个三角形三个内角度数的比为,
设三角形的三个内角分别是,,,
,解得,
.
此三角形是等腰直角三角形.
故选:.
8.如图所示,在三角形中,,,在上分别取点,使,,则图中的等腰三角形有
A.3个 B.4个 C.5个 D.6个
【解答】解:,,
,是等腰三角形,
,
是等腰三角形,
,
是等腰三角形,
,
是等腰三角形,
同理,是等腰三角形,
,
是等腰三角形,
故选:.
9.如图,已知中,,,,则等于
A. B. C. D.
【解答】解:,
,
,
,
,
,
即,
,
,
,
故选:.
10.下列命题中:
①等腰三角形底边的中点到两腰的距离相等
②如果两个三角形全等,则它们必是关于直线成轴对称的图形
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形
④等腰三角形是关于底边中线成轴对称的图形
⑤条线段是关于经过该线段中点的直线成轴对称的图形
正确命题的个数是
A.2 B.3 C.4 D.5
【解答】解:①等腰三角形底边的中点到两腰的距离相等,是真命题;
②如果两个三角形全等,则它们不一定关于直线成轴对称的图形,是假命题;
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形,是真命题;
④等腰三角形是关于底边中线所在的直线成轴对称的图形,是假命题;
⑤条线段是关于经过该线段中点的垂线成轴对称的图形,是假命题;
故选:.
二、填空题(每小题3分,共计30分)
11.等边三角形有 3 条对称轴 .
【解答】解: 等边三角形有 3 条对称轴 .
故答案为: 3 .
12.一个正多边形的每个内角为,则这个正多边形的每一个外角等于 72 度.
【解答】解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于
故答案为:72
13.一个三角形的两边长为3和6,若第三边取值范围为 第三边 .
【解答】解:根据三角形的三边关系可得:第三边,
则第三边,
故答案为:第三边.
14.等腰三角形的一个外角是,则其底角是 40 度.
【解答】解:与角相邻的内角度数为;
当角是底角时,,不符合三角形内角和定理,此种情况不成立;
当角是顶角时,底角的度数;
故此等腰三角形的底角为.
故填40.
15.如图,,,则 80 .
【解答】解:,,
,
.
故答案为:80.
16.已知点和关于轴对称,则 5 .
【解答】解:点与点关于轴对称,
,,
,
故答案为5.
17.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 11 .
【解答】解:由折叠的性质可知,,,
,
,
的周长,
即的周长为.
故答案为:11.
18.已知,如图中,,边,的垂直平分线分别交边于点、,连接与,则的度数为 20 度.
【解答】解:,
,
,,
,,
,,
,
.
故答案为:20.
19.直角三角形中两锐角平分线相交所成的角的度数是 或 .
【解答】解:如图,,
、分别是和的角平分线,
,
,
两锐角的平分线的夹角是或,
故答案为:或
20.如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 8 .
【解答】解:平分,
,
,
,
,
①,
过点作交于点,如图所示:
则,,
,
,
,
平分,
,
在与中,,
,
,,
②,
由①②可得,;
的周长为20,,
,
;
故答案为:8.
三、解答题(21题、22题各7分23题4题各8分,25题、26题、7题各10分)
21.已知,如图,点、、、在同一直线上,,,.
求证:,.
【解答】解:,,
,.
,
.
在和中,
.
,.
22.(1)请画出关于轴对称的△(其、、分别是、、的对应点,不写画法);
(2)直接写出、、三点的坐标:
(3)的面积是 .
【解答】解:(1)如图所示,△即为所求;
(2)点的坐标为、的坐标为、的坐标为;
(3)的面积是,
故答案为:.
23.已知:如图,,,,在同一直线上,,.求证:.
【解答】证明:作于,
(已知),
(三线合一),
又(已知),
(三线合一),
,即(等式的性质).
24.如图在直角中,,点是中点,连接,点为的中点,过点作交线段的延长线于点,连接.
(1)求证:;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于面积2倍的三角形.
【解答】证明:(1),
是直角三角形,是边上的中线,是的中点,
,
在和中,
,
;
(2)解:,
.
,,
,
四边形是平行四边形,
;
面积等于面积2倍的三角形有:,,,.
25.如图,中,,点在上,点在外部,且,,点在上,且,连接.
(1)求证:;
(2)若.且,求的长.
【解答】证明:(1),,
是等边三角形,
,,
,
,
,
,
,,
,
,
;
(2)解:.且,
设,则,
,
解得,
.
26.如图,和均为等边三角形,连接,.
(1)如图1,证明:;
(2)如图2,如果在边上,交于点,求的度数.
(3)如图3,在(2)的条件下,过作于,若,,求的长.
【解答】(1)证明:和均为等边三角形
,,,
,在和中,,
,
;
(2)解:由(1)得:,
,
,
,
,
,
;
(3)解:连接,在上截取,连接,如图3所示:
则是等边三角形,
,,
,,
在和中,,
,
,,
,
,,
,
,
,
,
,
,
,
,
.
27.在平面直角坐标系中,点在轴的正半轴上,点在轴正半轴上,且,满足等式.点从点出发,沿轴的正半轴运动,过点作轴的垂线.是垂线在第一象限内的一动点且.
(1)求,的值;
(2)若点在线段上,当,求点的坐标;
(3)若点在线段的延长线上,的垂直平分线交轴于点,并且恰好经过点,求此时的面积.
【解答】解:(1),
,,
解得,,;
(2)如图1,,,
,
在和中,
,
,
,
点的坐标为;
(3)连接、,作于,
设坐标为,根据,得到,
垂直平分,
,即,
,
解得:,(舍去),
,
设坐标为,
垂直平分,
,
在中,根据勾股定理得:,即,
解得:,
,
则.
一、选择题(每小题3分,共计30分)
1.下列图形中,不是轴对称图形的是
A. B.
C. D.
2.一个多边形的外角和与它的内角和相等,则多边形是
A.三角形 B.四边形 C.五边形 D.六边形
3.点关于轴对称的点的坐标是
A . B . C . D .
4.等腰三角形的顶角是,则它的底角是
A. B. C.或 D.或
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
6.到三角形三条边的距离都相等的点是这个三角形的
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
7.一个三角形三个内角的度数比为,这个三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
8.如图所示,在三角形中,,,在上分别取点,使,,则图中的等腰三角形有
A.3个 B.4个 C.5个 D.6个
9.如图,已知中,,,,则等于
A. B. C. D.
10.下列命题中:
①等腰三角形底边的中点到两腰的距离相等
②如果两个三角形全等,则它们必是关于直线成轴对称的图形
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形
④等腰三角形是关于底边中线成轴对称的图形
⑤条线段是关于经过该线段中点的直线成轴对称的图形
正确命题的个数是
A.2 B.3 C.4 D.5
二、填空题(每小题3分,共计30分)
11.等边三角形有 条对称轴 .
12.一个正多边形的每个内角为,则这个正多边形的每一个外角等于 度.
13.一个三角形的两边长为3和6,若第三边取值范围为 .
14.等腰三角形的一个外角是,则其底角是 度.
15.如图,,,则 .
16.已知点和关于轴对称,则 .
17.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 .
18.已知,如图中,,边,的垂直平分线分别交边于点、,连接与,则的度数为 度.
19.直角三角形中两锐角平分线相交所成的角的度数是 .
20.如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 .
三、解答题(21题、22题各7分23题4题各8分,25题、26题、7题各10分)
21.已知,如图,点、、、在同一直线上,,,.
求证:,.
22.(1)请画出关于轴对称的△(其、、分别是、、的对应点,不写画法);
(2)直接写出、、三点的坐标:
(3)的面积是 .
23.已知:如图,,,,在同一直线上,,.求证:.
24.如图在直角中,,点是中点,连接,点为的中点,过点作交线段的延长线于点,连接.
(1)求证:;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于面积2倍的三角形.
25.如图,中,,点在上,点在外部,且,,点在上,且,连接.
(1)求证:;
(2)若.且,求的长.
26.如图,和均为等边三角形,连接,.
(1)如图1,证明:;
(2)如图2,如果在边上,交于点,求的度数.
(3)如图3,在(2)的条件下,过作于,若,,求的长.
27.在平面直角坐标系中,点在轴的正半轴上,点在轴正半轴上,且,满足等式.点从点出发,沿轴的正半轴运动,过点作轴的垂线.是垂线在第一象限内的一动点且.
(1)求,的值;
(2)若点在线段上,当,求点的坐标;
(3)若点在线段的延长线上,的垂直平分线交轴于点,并且恰好经过点,求此时的面积.
2019-2020学年黑龙江省哈尔滨市尚志市八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共计30分)
1.下列图形中,不是轴对称图形的是
A. B.
C. D.
【解答】解:、不是轴对称图形,故此选项符合题意;
、是轴对称图形,故此选项不合题意;
、是轴对称图形,故此选项不合题意;
、是轴对称图形,故此选项不合题意;
故选:.
2.一个多边形的外角和与它的内角和相等,则多边形是
A.三角形 B.四边形 C.五边形 D.六边形
【解答】解:设多边形的边数为.
根据题意得:,
解得:.
故选:.
3.点关于轴对称的点的坐标是
A . B . C . D .
【解答】解:关于轴对称的点, 横坐标相同, 纵坐标互为相反数,
点关于轴对称的点的坐标是.
故选:.
4.等腰三角形的顶角是,则它的底角是
A. B. C.或 D.或
【解答】解:因为等腰三角形的两个底角相等,
又因为顶角是,
所以其底角为.
故选:.
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是
A.带①去 B.带②去 C.带③去 D.带①和②去
【解答】解:、带①去,仅保留了原三角形的一个角和部分边,不能得到与原来一样的三角形,故选项错误;
、带②去,仅保留了原三角形的一部分边,也是不能得到与原来一样的三角形,故选项错误;
、带③去,不但保留了原三角形的两个角还保留了其中一个边,符合判定,故选项正确;
、带①和②去,仅保留了原三角形的一个角和部分边,同样不能得到与原来一样的三角形,故选项错误.
故选:.
6.到三角形三条边的距离都相等的点是这个三角形的
A.三条中线的交点 B.三条高的交点
C.三条边的垂直平分线的交点 D.三条角平分线的交点
【解答】解:
角的平分线上的点到角的两边的距离相等,
到三角形的三边的距离相等的点是三条角平分线的交点.
故选:.
7.一个三角形三个内角的度数比为,这个三角形是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
【解答】解:一个三角形三个内角度数的比为,
设三角形的三个内角分别是,,,
,解得,
.
此三角形是等腰直角三角形.
故选:.
8.如图所示,在三角形中,,,在上分别取点,使,,则图中的等腰三角形有
A.3个 B.4个 C.5个 D.6个
【解答】解:,,
,是等腰三角形,
,
是等腰三角形,
,
是等腰三角形,
,
是等腰三角形,
同理,是等腰三角形,
,
是等腰三角形,
故选:.
9.如图,已知中,,,,则等于
A. B. C. D.
【解答】解:,
,
,
,
,
,
即,
,
,
,
故选:.
10.下列命题中:
①等腰三角形底边的中点到两腰的距离相等
②如果两个三角形全等,则它们必是关于直线成轴对称的图形
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形
④等腰三角形是关于底边中线成轴对称的图形
⑤条线段是关于经过该线段中点的直线成轴对称的图形
正确命题的个数是
A.2 B.3 C.4 D.5
【解答】解:①等腰三角形底边的中点到两腰的距离相等,是真命题;
②如果两个三角形全等,则它们不一定关于直线成轴对称的图形,是假命题;
③如果两个三角形关于某直线成轴对称,那么它们是全等三角形,是真命题;
④等腰三角形是关于底边中线所在的直线成轴对称的图形,是假命题;
⑤条线段是关于经过该线段中点的垂线成轴对称的图形,是假命题;
故选:.
二、填空题(每小题3分,共计30分)
11.等边三角形有 3 条对称轴 .
【解答】解: 等边三角形有 3 条对称轴 .
故答案为: 3 .
12.一个正多边形的每个内角为,则这个正多边形的每一个外角等于 72 度.
【解答】解:设此多边形为边形,
根据题意得:,
解得:,
这个正多边形的每一个外角等于
故答案为:72
13.一个三角形的两边长为3和6,若第三边取值范围为 第三边 .
【解答】解:根据三角形的三边关系可得:第三边,
则第三边,
故答案为:第三边.
14.等腰三角形的一个外角是,则其底角是 40 度.
【解答】解:与角相邻的内角度数为;
当角是底角时,,不符合三角形内角和定理,此种情况不成立;
当角是顶角时,底角的度数;
故此等腰三角形的底角为.
故填40.
15.如图,,,则 80 .
【解答】解:,,
,
.
故答案为:80.
16.已知点和关于轴对称,则 5 .
【解答】解:点与点关于轴对称,
,,
,
故答案为5.
17.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 11 .
【解答】解:由折叠的性质可知,,,
,
,
的周长,
即的周长为.
故答案为:11.
18.已知,如图中,,边,的垂直平分线分别交边于点、,连接与,则的度数为 20 度.
【解答】解:,
,
,,
,,
,,
,
.
故答案为:20.
19.直角三角形中两锐角平分线相交所成的角的度数是 或 .
【解答】解:如图,,
、分别是和的角平分线,
,
,
两锐角的平分线的夹角是或,
故答案为:或
20.如图,中,,和分别为和的角平分线,若的周长为20,,则的长为 8 .
【解答】解:平分,
,
,
,
,
①,
过点作交于点,如图所示:
则,,
,
,
,
平分,
,
在与中,,
,
,,
②,
由①②可得,;
的周长为20,,
,
;
故答案为:8.
三、解答题(21题、22题各7分23题4题各8分,25题、26题、7题各10分)
21.已知,如图,点、、、在同一直线上,,,.
求证:,.
【解答】解:,,
,.
,
.
在和中,
.
,.
22.(1)请画出关于轴对称的△(其、、分别是、、的对应点,不写画法);
(2)直接写出、、三点的坐标:
(3)的面积是 .
【解答】解:(1)如图所示,△即为所求;
(2)点的坐标为、的坐标为、的坐标为;
(3)的面积是,
故答案为:.
23.已知:如图,,,,在同一直线上,,.求证:.
【解答】证明:作于,
(已知),
(三线合一),
又(已知),
(三线合一),
,即(等式的性质).
24.如图在直角中,,点是中点,连接,点为的中点,过点作交线段的延长线于点,连接.
(1)求证:;
(2)在不添加任何辅助线的情况下,请直接写出所有面积等于面积2倍的三角形.
【解答】证明:(1),
是直角三角形,是边上的中线,是的中点,
,
在和中,
,
;
(2)解:,
.
,,
,
四边形是平行四边形,
;
面积等于面积2倍的三角形有:,,,.
25.如图,中,,点在上,点在外部,且,,点在上,且,连接.
(1)求证:;
(2)若.且,求的长.
【解答】证明:(1),,
是等边三角形,
,,
,
,
,
,
,,
,
,
;
(2)解:.且,
设,则,
,
解得,
.
26.如图,和均为等边三角形,连接,.
(1)如图1,证明:;
(2)如图2,如果在边上,交于点,求的度数.
(3)如图3,在(2)的条件下,过作于,若,,求的长.
【解答】(1)证明:和均为等边三角形
,,,
,在和中,,
,
;
(2)解:由(1)得:,
,
,
,
,
,
;
(3)解:连接,在上截取,连接,如图3所示:
则是等边三角形,
,,
,,
在和中,,
,
,,
,
,,
,
,
,
,
,
,
,
,
.
27.在平面直角坐标系中,点在轴的正半轴上,点在轴正半轴上,且,满足等式.点从点出发,沿轴的正半轴运动,过点作轴的垂线.是垂线在第一象限内的一动点且.
(1)求,的值;
(2)若点在线段上,当,求点的坐标;
(3)若点在线段的延长线上,的垂直平分线交轴于点,并且恰好经过点,求此时的面积.
【解答】解:(1),
,,
解得,,;
(2)如图1,,,
,
在和中,
,
,
,
点的坐标为;
(3)连接、,作于,
设坐标为,根据,得到,
垂直平分,
,即,
,
解得:,(舍去),
,
设坐标为,
垂直平分,
,
在中,根据勾股定理得:,即,
解得:,
,
则.
同课章节目录
