21.4 圆周角 课件(20张PPT)
文档属性
| 名称 | 21.4 圆周角 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览





文档简介
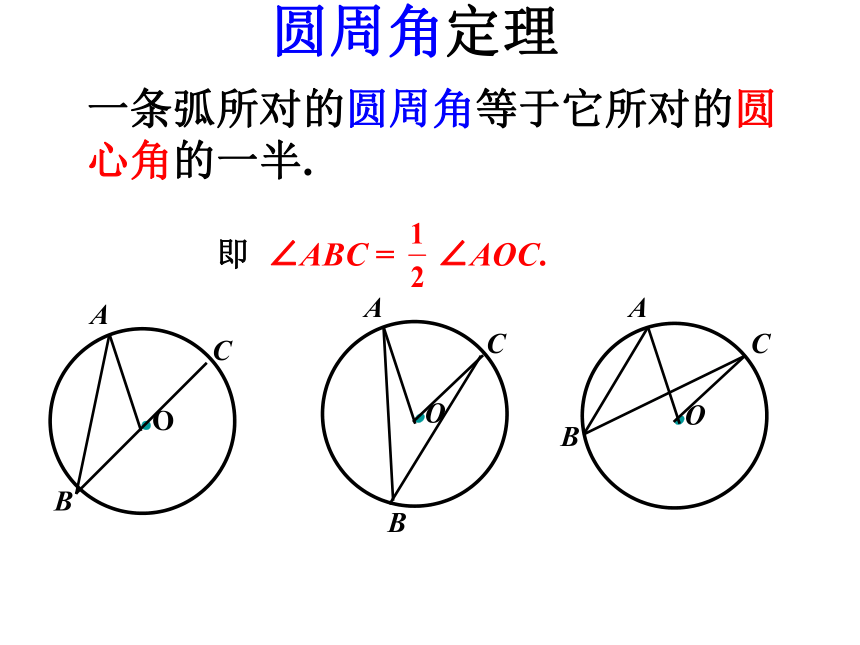
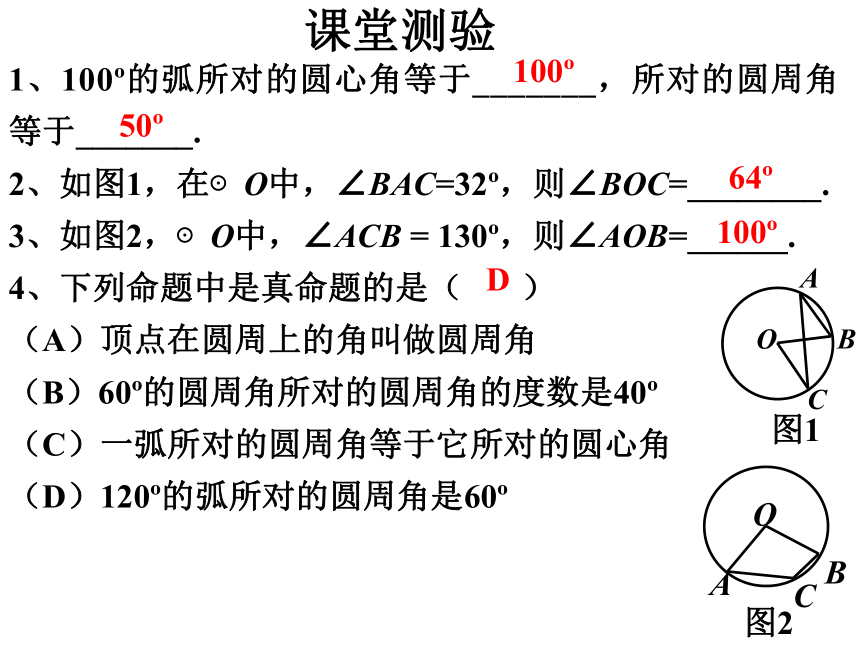
课件20张PPT。 圆周角特征:① 角的顶点在圆上.② 角的两边都与圆相交.圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半.1、100o的弧所对的圆心角等于_______,所对的圆周角等于_______.
2、如图1,在⊙O中,∠BAC=32o,则∠BOC=________.
3、如图2,⊙O中,∠ACB = 130o,则∠AOB=______.
4、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角
(B)60o的圆周角所对的圆周角的度数是40o
(C)一弧所对的圆周角等于它所对的圆心角
(D)120o的弧所对的圆周角是60o课堂测验100o50o64o100oD推论1:
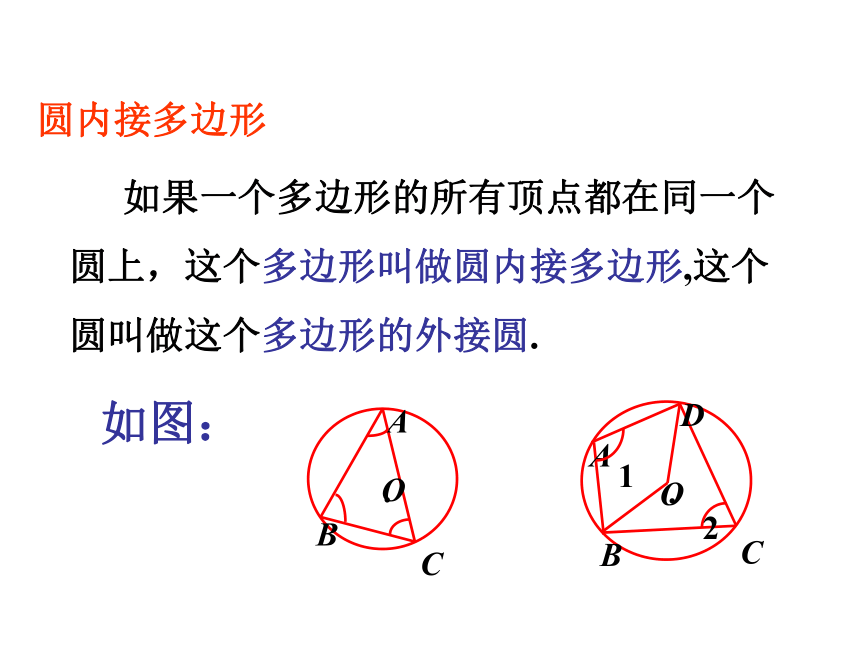
同弧或等弧所对的圆周角相等.同圆或等圆中,相等的圆周角所对的弧也相等.圆内接多边形
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.如图:圆内接四边形的性质如图四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆 .
∵ ∠A所对弧为弧BCD,∠C所对的弧为弧BAD,又弧 BCD与弧BAD所对的圆心角的和是周角,
∴∠A+∠C= =180°.
同理 ∠B+∠D=180°.ABCD·O12这样,利用圆周角定理,我们得到关于圆内接四边形的一个性质: 推论2:
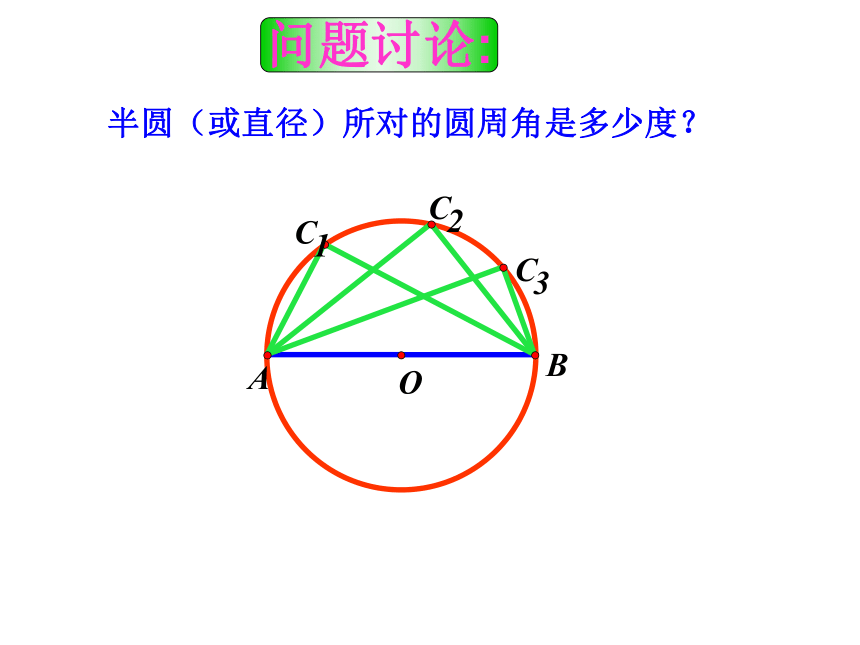
圆内接四边形的对角互补.半圆(或直径)所对的圆周角是多少度? 问题讨论:90°的圆周角所对的弦是什么? 问题讨论:如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?想一想:证明:
∵OA=OB=OC,
∴ △AOC、△BOC都是等腰三角形,
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°,
而 ∠ACB=∠OCA+∠OCB
∴ ∠OAC+∠OBC+ ∠OCA+∠OCB =180°
∴2( ∠OCA+∠OCB ) =180°
即: ∠ACB=∠OCA+∠OCB =90°分析解答:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径. 例1 如图,AB是⊙O的直径,∠A=80°.
求∠ABC的度数. 解 :∵ AB是⊙O的直径,
而直径所对的圆周角是直角,
∴ ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°.
∴ ∠ABC的度数是10°.例 题例2 已知:如图21-23,在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,求BC,AD和BD的长.
解:∵AB为直径,∴∠ACB=∠ADB=90°.在Rt△ACB中,∵ CD平分∠ACB ,在等腰直角三角形ADB中,练习:利用三角尺可以确认图中的弦AB是圆的直径,为什么?你能用这种方法确定一个圆形工件的圆心吗?解:因为∠C=90°,当A、B分别在三角尺的两直角边上时,AB为圆的直径.(直径所对的圆周角是直角)
可以用这种方法确定一个圆形工件的圆心.原理如上所述.如图,四边形ABCD是⊙O的内接四边形,∠CBE是它的一个外角.若∠D=100°,求∠CBE的度数.解:∵四边形ABCD是⊙O的内接四边形,且∠D=100°.
∴∠ABC+∠D=180°.(圆内接四边形的对角互补)
∴∠ABC=80°.
∴∠CBE=180°-∠ABC=100°.
即∠CBE的度数为100°.
四边形ABCD内接于⊙O,
则∠A+∠C=______ , ∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,∠CDE=______ 180° 180° 100°80°小结半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.推论:圆内接四边形的对角互补.顶点在圆上,并且两边都与圆相交的角叫做圆周角.一条弧所对的圆周角等于它所对的圆心角的一半.同弧或等弧所对的圆周角相等.同圆或等圆中,相等的圆周角所对的弧也相等.
2、如图1,在⊙O中,∠BAC=32o,则∠BOC=________.
3、如图2,⊙O中,∠ACB = 130o,则∠AOB=______.
4、下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角
(B)60o的圆周角所对的圆周角的度数是40o
(C)一弧所对的圆周角等于它所对的圆心角
(D)120o的弧所对的圆周角是60o课堂测验100o50o64o100oD推论1:
同弧或等弧所对的圆周角相等.同圆或等圆中,相等的圆周角所对的弧也相等.圆内接多边形
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.如图:圆内接四边形的性质如图四边形ABCD是⊙O的内接四边形,⊙O是四边形ABCD的外接圆 .
∵ ∠A所对弧为弧BCD,∠C所对的弧为弧BAD,又弧 BCD与弧BAD所对的圆心角的和是周角,
∴∠A+∠C= =180°.
同理 ∠B+∠D=180°.ABCD·O12这样,利用圆周角定理,我们得到关于圆内接四边形的一个性质: 推论2:
圆内接四边形的对角互补.半圆(或直径)所对的圆周角是多少度? 问题讨论:90°的圆周角所对的弦是什么? 问题讨论:如图,线段AB是⊙O的直径,点C是⊙O上任意一点(除点A、B),那么,∠ACB就是直径AB所对的圆周角.想想看,∠ACB会是怎么样的角?想一想:证明:
∵OA=OB=OC,
∴ △AOC、△BOC都是等腰三角形,
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°,
而 ∠ACB=∠OCA+∠OCB
∴ ∠OAC+∠OBC+ ∠OCA+∠OCB =180°
∴2( ∠OCA+∠OCB ) =180°
即: ∠ACB=∠OCA+∠OCB =90°分析解答:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径. 例1 如图,AB是⊙O的直径,∠A=80°.
求∠ABC的度数. 解 :∵ AB是⊙O的直径,
而直径所对的圆周角是直角,
∴ ∠ABC=180°-∠A-∠ACB
=180°-80°-90°
=10°.
∴ ∠ABC的度数是10°.例 题例2 已知:如图21-23,在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,求BC,AD和BD的长.
解:∵AB为直径,∴∠ACB=∠ADB=90°.在Rt△ACB中,∵ CD平分∠ACB ,在等腰直角三角形ADB中,练习:利用三角尺可以确认图中的弦AB是圆的直径,为什么?你能用这种方法确定一个圆形工件的圆心吗?解:因为∠C=90°,当A、B分别在三角尺的两直角边上时,AB为圆的直径.(直径所对的圆周角是直角)
可以用这种方法确定一个圆形工件的圆心.原理如上所述.如图,四边形ABCD是⊙O的内接四边形,∠CBE是它的一个外角.若∠D=100°,求∠CBE的度数.解:∵四边形ABCD是⊙O的内接四边形,且∠D=100°.
∴∠ABC+∠D=180°.(圆内接四边形的对角互补)
∴∠ABC=80°.
∴∠CBE=180°-∠ABC=100°.
即∠CBE的度数为100°.
四边形ABCD内接于⊙O,
则∠A+∠C=______ , ∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,∠CDE=______ 180° 180° 100°80°小结半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.推论:圆内接四边形的对角互补.顶点在圆上,并且两边都与圆相交的角叫做圆周角.一条弧所对的圆周角等于它所对的圆心角的一半.同弧或等弧所对的圆周角相等.同圆或等圆中,相等的圆周角所对的弧也相等.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
