22.2 圆的切线 课件(44张PPT)
文档属性
| 名称 | 22.2 圆的切线 课件(44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 793.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 09:49:42 | ||
图片预览








文档简介
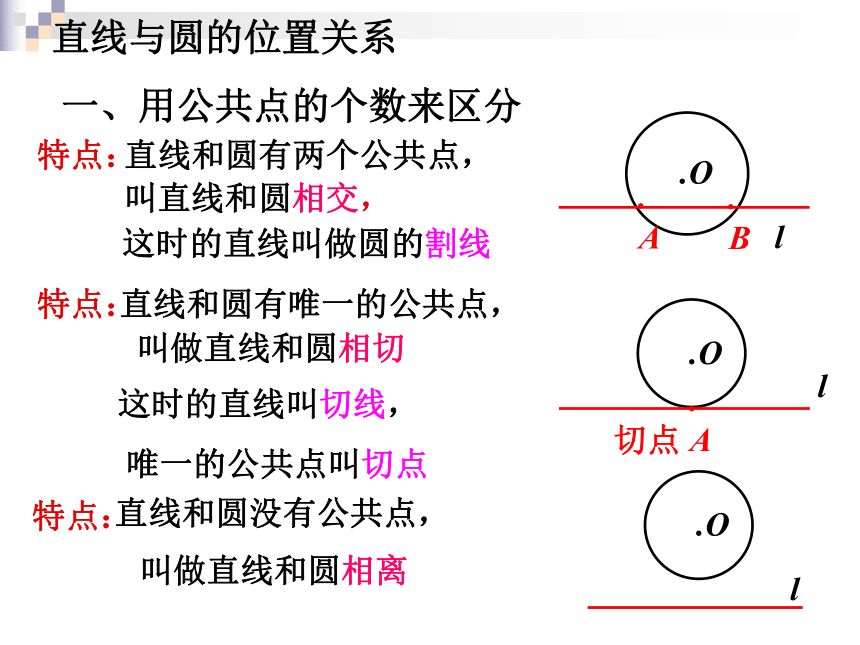
课件44张PPT。圆的切线第一课时.Ol特点:.O叫做直线和圆相离直线和圆没有公共点,l特点:直线和圆有唯一的公共点,叫做直线和圆相切这时的直线叫切线,
唯一的公共点叫切点.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线直线与圆的位置关系
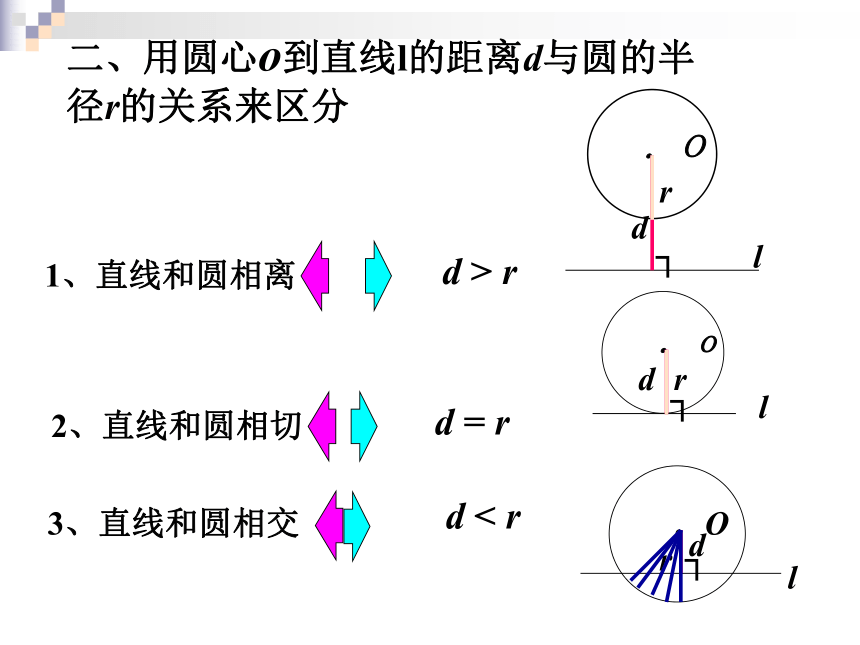
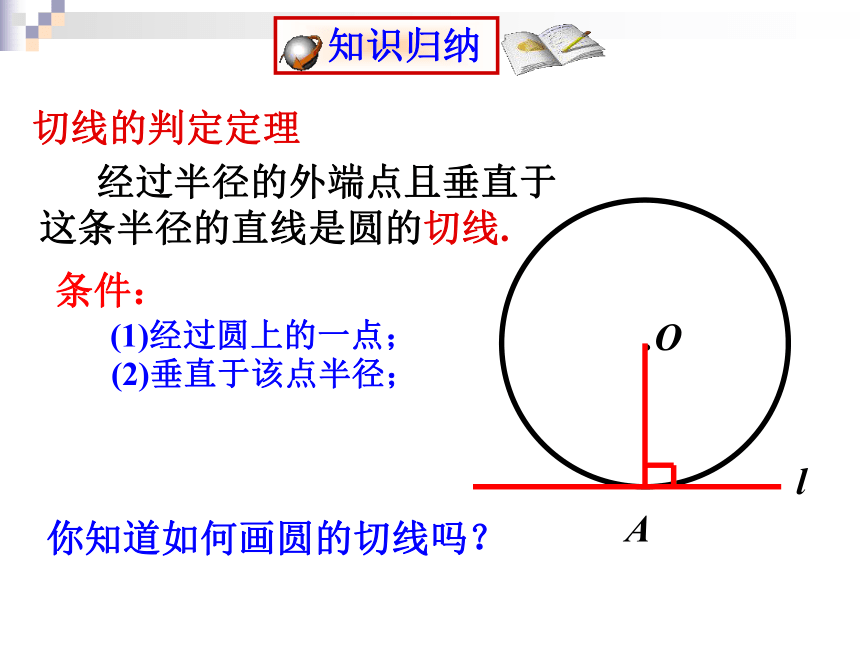
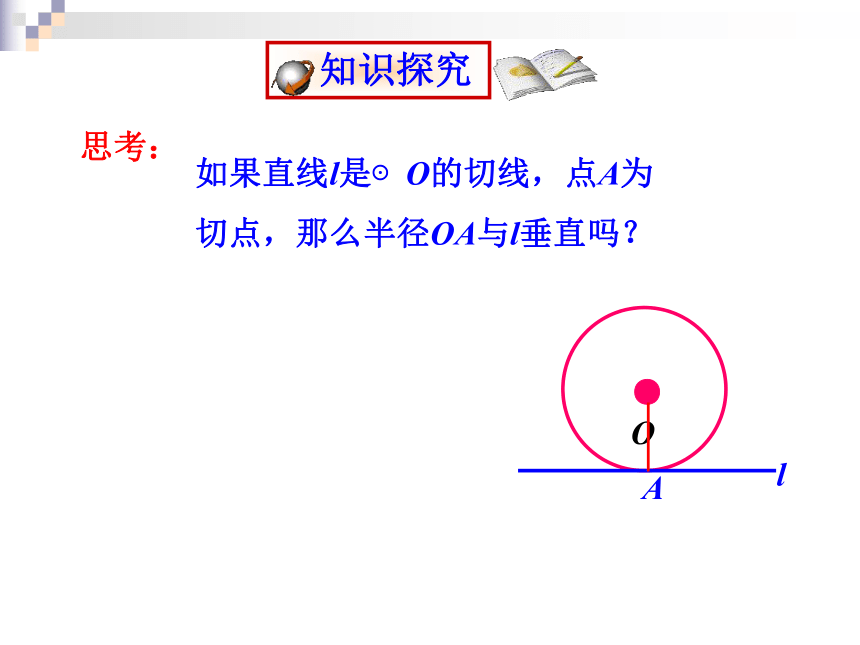
一、用公共点的个数来区分.A.A.B切点2、直线和圆相切d = r3、直线和圆相交d < rdr二、用圆心o到直线l的距离d与圆的半径r的关系来区分1、直线和圆相离d > r问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的?问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的?切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.如图:判断下列图形中的直 线a是否是圆的切线一般情况下,要证明一条直线为圆的切线,它过半径外端是已知给出时,只需证明该直线垂直于半径..OlA切线的判定定理 经过半径的外端点且垂直于这条半径的直线是圆的切线.条件:(1)经过圆上的一点;(2)垂直于该点半径;你知道如何画圆的切线吗? 如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗? 思考:Al.OlA切线的性质定理推理格式
∵直线l是⊙ O 的切线
∴ OA⊥l圆的切线垂直于经过切点的半径. 你能证明这个定理吗?直线AB经过圆O上的C,并且OA=OBAC=BC.
求证:直线AB是圆O 的切线证明一条直线是圆的切线时:
直线与圆有交点时,连接交点与圆心,证垂直.解:直线AC与⊙O相切.
理由如下:∴AB2+AC2=BC2.∴△ABC为直角三角形,∠BAC=900.∵AB为⊙O的直径,∴直线AC经过⊙O半径的外端A.∴直线AC与⊙O相切,A为切点.方法归纳:证明一条直线是圆的切线的常见方法有两种:(1)当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“作半径,证垂直”.(2)当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.如图AB是⊙O的切线,点A是⊙O上的一点则 AB ___ OA.
AlO切线的性质:
圆的切线垂直于经过切点的半径.
⊥如果l是 ⊙O 的切线,A 为切点,那么AM⊥OA.
你能说明理由吗?OM反证法:假设l与OA不垂直
则过点O作OM⊥l,垂足为M
根据垂线段最短的性质, 得OM<OA,
即圆心O到直线l的距离d<R
∴直线l 与⊙O 相交
这与已知“l是 ⊙O 的切线”矛盾
∴假设不成立,即OA⊥l例2 如图所示,AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数.解:连接OA∵ AB是⊙O的弦∴ OA⊥AC即∠OAC=90°∴∠OAB=90°-∠CAB=46°又∵OA=OB∴∠OBA=∠OAB=46°1、判断题:×(1) 垂直于圆的半径的直线一定是这个圆的切线 (2) 过圆的半径的外端的直线一定是这个圆的切线 ×2.如图,AB是⊙O的直径,∠B=45°,AC=AB, AC是⊙O的切线吗?为什么? 解:AC是⊙O的切线 。理由如下:又∵∠BAC+∠B+∠C = 180°∵ AC=AB , ∠B=45°(已知) ∴ AC⊥AB∴AC是⊙O的切线∴∠C=∠B=45°(等边对等角) ∴∠ BAC = 180°-∠B-∠C=90°ABC3.PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,
求∠ACB的度数.1、如何判定一条直线是已知圆的切线?(1)和圆只有一个公共点的直线是圆的切线;(2)和圆心的距离等于半径的直线是圆的切线;(3)过半径外端且和半径垂直的直线是圆的切线;(d=r)A 、经过圆上的一点;B、 垂直于半径;2、圆的切线有什么性质?圆的切线垂直于经过切点的半径.第二课时1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习
惯,提高学生综合运用知识解题的能力,培养数
形结合的思想.学习目标1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.O温故而知新 OABP如何用圆规和直尺作出这两条切线呢?.思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?做一做O ·PABO?? ? 议一议
如图 ,PA,PB 是 ⊙O 的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的
对称轴是什么?
(2)在这个图中你能发现相等的线段吗?说说
你的理由.过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.·OPAB切线与切线长是一回事吗?它们有什么区别与联系呢?切线长概念切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.过圆外一点所画的圆的两条切线长相等. 几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法PA =PB∠OPA=∠OPBAPOB若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA=PB,∠OPA=∠OPB.
∴△PAB是等腰三角形,PM为顶角的平分线.
∴OP垂直平分AB.探一探.PBAO(3)连接圆心和圆外一点(2)连接两切点(1)分别连接圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形.探究:PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.
BAPOCE(1)写出图中所有的垂直关系OA⊥PA OB⊥PB AB⊥OP(2)写出图中与∠OAC相等的角∠OAC=∠OBC=∠APC=∠BPCD△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP(4)写出图中所有的等腰三角形△ABP,△AOB(3)写出图中所有的全等三角形
BAPOCED三角形内切圆内切圆圆心:三角形三个内角平分线的交点
内切圆的半径:交点到三角形任意一边的垂直距离ABC这个三角形称为这个圆的外切三角形.内切圆圆心叫做三角形的内心.例3 如图,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.例题精讲解:连接 OD,OE,OF,设 OD = r.
在 Rt△ABC 中,AC = 10,BC = 24,
∵ ⊙O 分别与 AB,BC,CA 相切于点 D,E,F,∴ OD⊥AB,OE⊥BC,OF⊥AC,BE =BD,
AF =AD, CE =CF.
又∵ ∠C = 90° ,∴ 四边形OECF 为正方形.
∴EC = FC = r. BE = 24 –r,AF = 10 - r.
∴AB =BD + AD = BE + AF = 34 - 2r = 26.
∴ r = 4,
即 ⊙O半径为4.例4 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x,则AE=x∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.由BD+CD=BC可得
13-x+9-x=14,解得x=4.∴ AF=4 cm, BD=5 cm, CE=9 cm.如图 ,四边形 ABCD 的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.证明:由切线长定理得
AL=AP,LB=MB,NC=MC,DN=DP,
∴AP+MB+MC+DP=AL+LB+NC+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
的和相等.N合作交流1.如图,PA,PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠PAB等于( ) A.60° B.90°
C.120° D.150°A课堂检测2. PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.如果PA=4cm,PD=2cm,求半径OA的长.【解析】设OA=xcm;在Rt△OAP中,OA=xcm,OP=OD+PD=(x+2)cm,PA=4cm,由勾股定理,得
PA2+OA2=OP2,即42+x2=(x+2)2,整理,得x=3.所以,半径OA的长为3cm.通过本课时的学习,我们学会了?盘点收获
唯一的公共点叫切点.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线直线与圆的位置关系
一、用公共点的个数来区分.A.A.B切点2、直线和圆相切d = r3、直线和圆相交d < rdr二、用圆心o到直线l的距离d与圆的半径r的关系来区分1、直线和圆相离d > r问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的?问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的?切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.如图:判断下列图形中的直 线a是否是圆的切线一般情况下,要证明一条直线为圆的切线,它过半径外端是已知给出时,只需证明该直线垂直于半径..OlA切线的判定定理 经过半径的外端点且垂直于这条半径的直线是圆的切线.条件:(1)经过圆上的一点;(2)垂直于该点半径;你知道如何画圆的切线吗? 如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗? 思考:Al.OlA切线的性质定理推理格式
∵直线l是⊙ O 的切线
∴ OA⊥l圆的切线垂直于经过切点的半径. 你能证明这个定理吗?直线AB经过圆O上的C,并且OA=OBAC=BC.
求证:直线AB是圆O 的切线证明一条直线是圆的切线时:
直线与圆有交点时,连接交点与圆心,证垂直.解:直线AC与⊙O相切.
理由如下:∴AB2+AC2=BC2.∴△ABC为直角三角形,∠BAC=900.∵AB为⊙O的直径,∴直线AC经过⊙O半径的外端A.∴直线AC与⊙O相切,A为切点.方法归纳:证明一条直线是圆的切线的常见方法有两种:(1)当直线和圆有一个公共点时,把圆心和这个公共点连接起来,然后证明直线垂直于这条半径,简称“作半径,证垂直”.(2)当直线和圆的公共点没有明确时,可过圆心作直线的垂线,再证圆心到直线的距离等于半径,简称“作垂直,证半径”.如图AB是⊙O的切线,点A是⊙O上的一点则 AB ___ OA.
AlO切线的性质:
圆的切线垂直于经过切点的半径.
⊥如果l是 ⊙O 的切线,A 为切点,那么AM⊥OA.
你能说明理由吗?OM反证法:假设l与OA不垂直
则过点O作OM⊥l,垂足为M
根据垂线段最短的性质, 得OM<OA,
即圆心O到直线l的距离d<R
∴直线l 与⊙O 相交
这与已知“l是 ⊙O 的切线”矛盾
∴假设不成立,即OA⊥l例2 如图所示,AB是⊙O的弦,AC切⊙于点A,且∠BAC=54°,求∠OBA的度数.解:连接OA∵ AB是⊙O的弦∴ OA⊥AC即∠OAC=90°∴∠OAB=90°-∠CAB=46°又∵OA=OB∴∠OBA=∠OAB=46°1、判断题:×(1) 垂直于圆的半径的直线一定是这个圆的切线 (2) 过圆的半径的外端的直线一定是这个圆的切线 ×2.如图,AB是⊙O的直径,∠B=45°,AC=AB, AC是⊙O的切线吗?为什么? 解:AC是⊙O的切线 。理由如下:又∵∠BAC+∠B+∠C = 180°∵ AC=AB , ∠B=45°(已知) ∴ AC⊥AB∴AC是⊙O的切线∴∠C=∠B=45°(等边对等角) ∴∠ BAC = 180°-∠B-∠C=90°ABC3.PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,
求∠ACB的度数.1、如何判定一条直线是已知圆的切线?(1)和圆只有一个公共点的直线是圆的切线;(2)和圆心的距离等于半径的直线是圆的切线;(3)过半径外端且和半径垂直的直线是圆的切线;(d=r)A 、经过圆上的一点;B、 垂直于半径;2、圆的切线有什么性质?圆的切线垂直于经过切点的半径.第二课时1.理解切线长的概念,掌握切线长定理.
2.学会运用切线长定理解有关问题.
3.通过对例题的分析,培养学生分析总结问题的习
惯,提高学生综合运用知识解题的能力,培养数
形结合的思想.学习目标1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.O温故而知新 OABP如何用圆规和直尺作出这两条切线呢?.思考:已画出切线PA,PB,A,B为切点,则∠OAP=90°,
连接OP,可知A,B 除了在⊙O上,还在怎样的圆上?做一做O ·PABO?? ? 议一议
如图 ,PA,PB 是 ⊙O 的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的
对称轴是什么?
(2)在这个图中你能发现相等的线段吗?说说
你的理由.过圆外一点作圆的切线,这点和切点之间的线段长叫做这点到圆的切线长.·OPAB切线与切线长是一回事吗?它们有什么区别与联系呢?切线长概念切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现什么?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.过圆外一点所画的圆的两条切线长相等. 几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法PA =PB∠OPA=∠OPBAPOB若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA=PB,∠OPA=∠OPB.
∴△PAB是等腰三角形,PM为顶角的平分线.
∴OP垂直平分AB.探一探.PBAO(3)连接圆心和圆外一点(2)连接两切点(1)分别连接圆心和切点反思:在解决有关圆的切线长问题时,往往需要我们构建基本图形.探究:PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.
BAPOCE(1)写出图中所有的垂直关系OA⊥PA OB⊥PB AB⊥OP(2)写出图中与∠OAC相等的角∠OAC=∠OBC=∠APC=∠BPCD△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP(4)写出图中所有的等腰三角形△ABP,△AOB(3)写出图中所有的全等三角形
BAPOCED三角形内切圆内切圆圆心:三角形三个内角平分线的交点
内切圆的半径:交点到三角形任意一边的垂直距离ABC这个三角形称为这个圆的外切三角形.内切圆圆心叫做三角形的内心.例3 如图,Rt△ABC 的两条直角边 AC = 10,BC = 24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求 ⊙O 的半径.例题精讲解:连接 OD,OE,OF,设 OD = r.
在 Rt△ABC 中,AC = 10,BC = 24,
∵ ⊙O 分别与 AB,BC,CA 相切于点 D,E,F,∴ OD⊥AB,OE⊥BC,OF⊥AC,BE =BD,
AF =AD, CE =CF.
又∵ ∠C = 90° ,∴ 四边形OECF 为正方形.
∴EC = FC = r. BE = 24 –r,AF = 10 - r.
∴AB =BD + AD = BE + AF = 34 - 2r = 26.
∴ r = 4,
即 ⊙O半径为4.例4 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x,则AE=x∴CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x.由BD+CD=BC可得
13-x+9-x=14,解得x=4.∴ AF=4 cm, BD=5 cm, CE=9 cm.如图 ,四边形 ABCD 的四条边都与 ⊙O 相切,图中的线段之间有哪些等量关系?与同伴进行交流.证明:由切线长定理得
AL=AP,LB=MB,NC=MC,DN=DP,
∴AP+MB+MC+DP=AL+LB+NC+DN,
即AD+BC=AB+CD,
补充:圆的外切四边形的两组对边
的和相等.N合作交流1.如图,PA,PB是⊙O的切线,切点分别是A,B,如果∠P=60°,那么∠PAB等于( ) A.60° B.90°
C.120° D.150°A课堂检测2. PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于点C.如果PA=4cm,PD=2cm,求半径OA的长.【解析】设OA=xcm;在Rt△OAP中,OA=xcm,OP=OD+PD=(x+2)cm,PA=4cm,由勾股定理,得
PA2+OA2=OP2,即42+x2=(x+2)2,整理,得x=3.所以,半径OA的长为3cm.通过本课时的学习,我们学会了?盘点收获
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
