人教版八年级上册第十三章轴对称13.1.2线段垂直平分线的性质课件 (17张PPT)
文档属性
| 名称 | 人教版八年级上册第十三章轴对称13.1.2线段垂直平分线的性质课件 (17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 133.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
第1课时 线段的垂直平分线的性质和判定
1.理解并掌握线段的垂直平分线的性质和判定方法.
(重点)
2.会用尺规过一点作已知直线的垂线.
3.灵活运用线段的垂直平分线的性质和判定解决实际问题.(难点)
学习目标
知识回顾
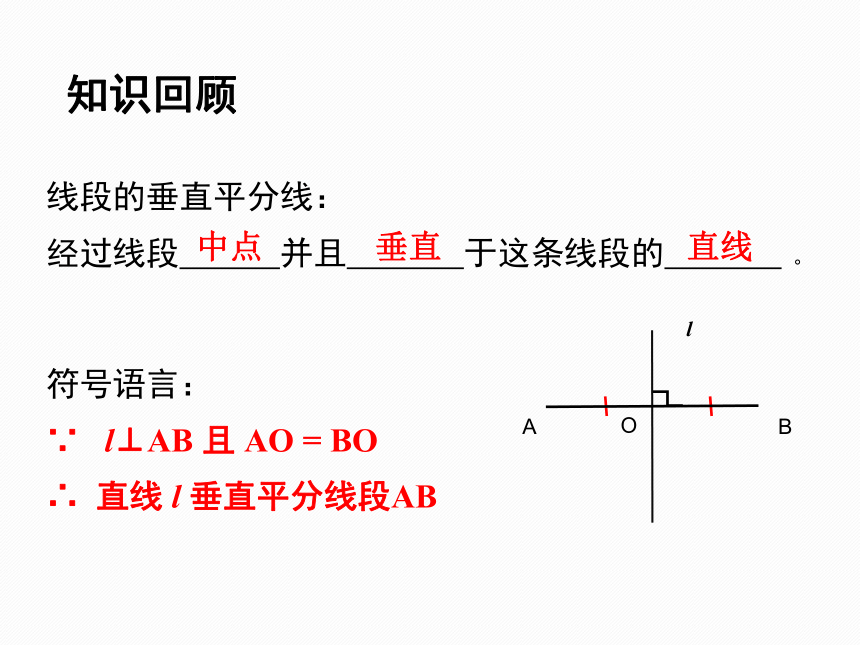
线段的垂直平分线:
经过线段 并且 于这条线段的 。
中点
垂直
直线
O
l
A
B
符号语言:
∵ l⊥AB 且 AO = BO
∴ 直线 l 垂直平分线段AB
=
=
=
阅读教材P61的内容,解决下列问题:
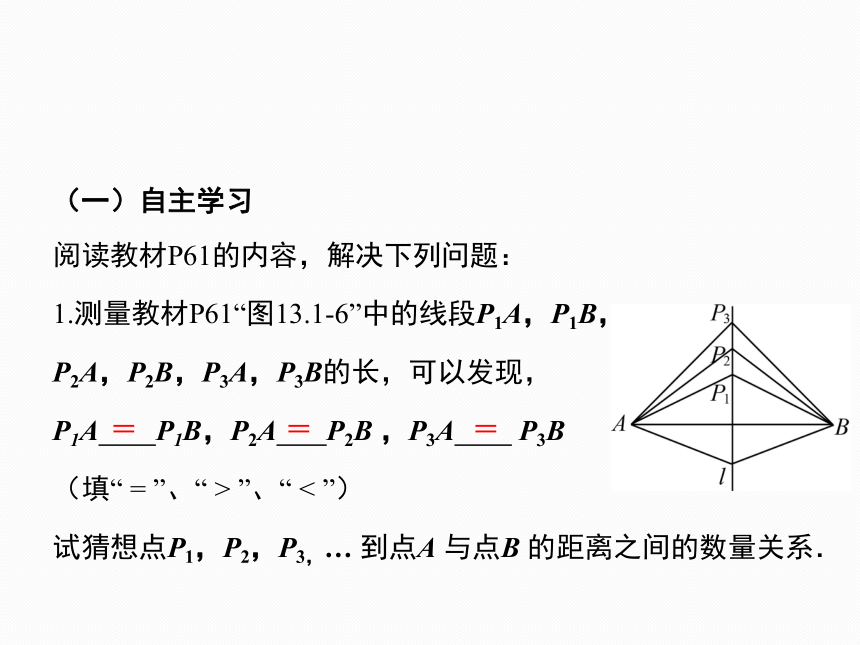
1.测量教材P61“图13.1-6”中的线段P1A,P1B,
P2A,P2B,P3A,P3B的长,可以发现,
P1A P1B,P2A P2B ,P3A P3B
(填“ = ”、“ > ”、“ < ”)
试猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
(一)自主学习
(二)归纳猜想
归纳:线段垂直平分线上的点与这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
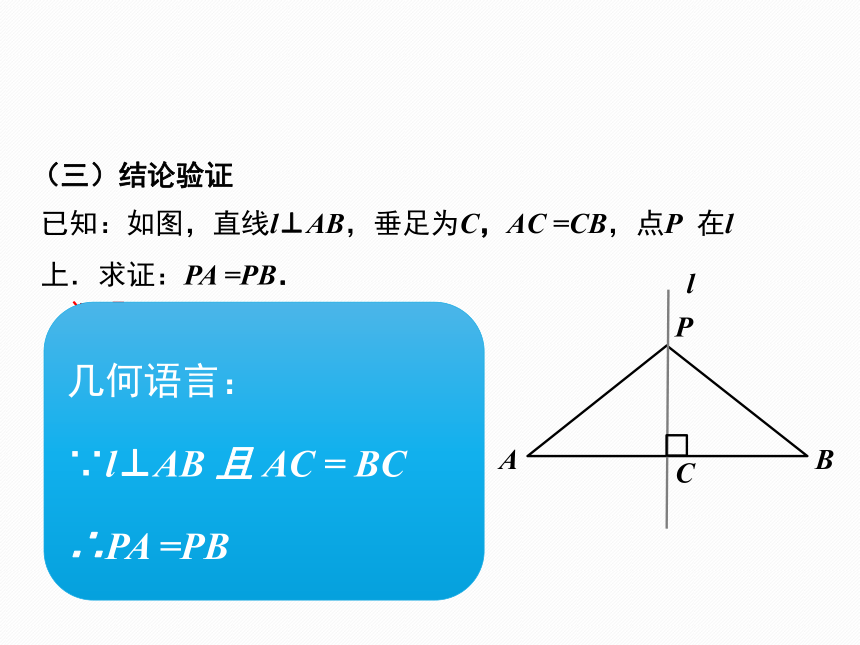
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
P
A
B
l
C
(三)结论验证
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
在△PCA 与△PCB中,
AC =CB
∠PCA =∠PCB
PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
几何语言:
∵l⊥AB 且 AC = BC
∴PA =PB
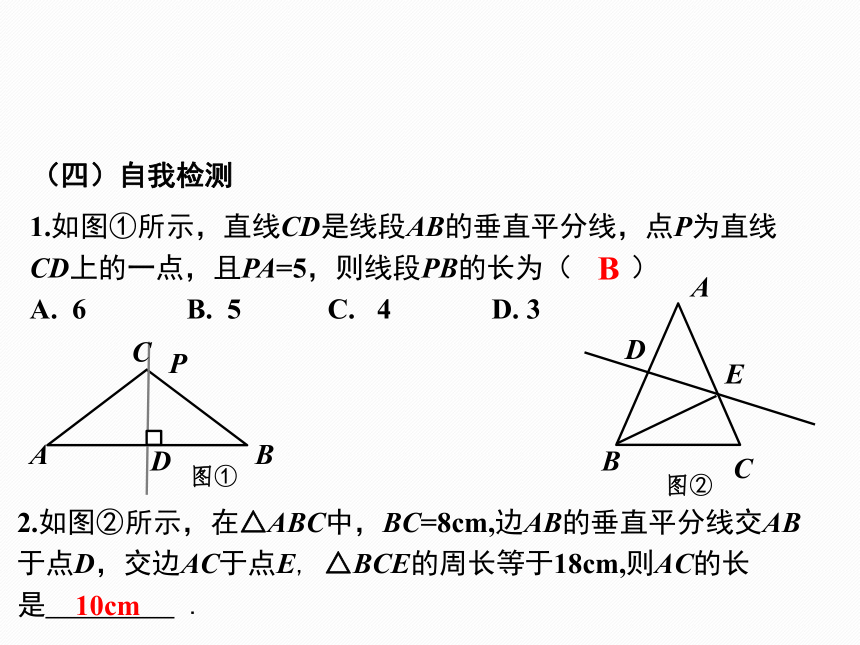
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
(四)自我检测
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
合作探究一
P
A
B
C
证法一:取AB中点C,连接PC。
∴AC=BC
在△PCA 和△PCB 中,
PA=PB
PC=PC
AC=BC
∴ △PCA ≌△PCB(SSS).
∴ ∠PCA =∠PCB =90°
即 PC⊥AB,
又点C为AB中点
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
证法二:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB
PC =PC
∴ Rt△PCA ≌ Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
证法三:过点P 作∠APB的平分线C.
则∠1=∠2.
在△PCA 和△PCB 中,
PA =PB
∠1=∠2
PC =PC
∴ △PCA ≌ △PCB(SAS).
∴ AC =BC.∠PCA=∠PCB=90°
∴ 点P 在线段AB 的垂直平分线上.
1
2
P
A
B
C
证法四:过点P 作AB 的垂直平分线PC.
∵ AC =BC.
∠PCA=∠PCB=90°
∴ 点P 在线段AB 的垂直平分线上.
A
P
B
D
(1)
A
P
B
D
(2)
一般情况下,“过点P作AB的垂直平分线”是不可能实现的。
几何语言:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳:与线段两个端点距离相等的点在这条线段的垂直平分线上
尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
直线CF就是所求作的垂线.
F
合作探究二
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
想一想:
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 DE的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
1.如图所示,AC=AD ,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
2.在锐角三角形ABC内一点P,满足PA=PB=PC,
则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
当堂检测
A
B
C
M
3.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
4.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
第3题图
第4题图
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
13.1.2 线段的垂直平分线的性质
第十三章 轴对称
第1课时 线段的垂直平分线的性质和判定
1.理解并掌握线段的垂直平分线的性质和判定方法.
(重点)
2.会用尺规过一点作已知直线的垂线.
3.灵活运用线段的垂直平分线的性质和判定解决实际问题.(难点)
学习目标
知识回顾
线段的垂直平分线:
经过线段 并且 于这条线段的 。
中点
垂直
直线
O
l
A
B
符号语言:
∵ l⊥AB 且 AO = BO
∴ 直线 l 垂直平分线段AB
=
=
=
阅读教材P61的内容,解决下列问题:
1.测量教材P61“图13.1-6”中的线段P1A,P1B,
P2A,P2B,P3A,P3B的长,可以发现,
P1A P1B,P2A P2B ,P3A P3B
(填“ = ”、“ > ”、“ < ”)
试猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
(一)自主学习
(二)归纳猜想
归纳:线段垂直平分线上的点与这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.求证:PA =PB.
P
A
B
l
C
(三)结论验证
证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
在△PCA 与△PCB中,
AC =CB
∠PCA =∠PCB
PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
几何语言:
∵l⊥AB 且 AC = BC
∴PA =PB
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
(四)自我检测
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平分线上.
合作探究一
P
A
B
C
证法一:取AB中点C,连接PC。
∴AC=BC
在△PCA 和△PCB 中,
PA=PB
PC=PC
AC=BC
∴ △PCA ≌△PCB(SSS).
∴ ∠PCA =∠PCB =90°
即 PC⊥AB,
又点C为AB中点
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
证法二:过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB
PC =PC
∴ Rt△PCA ≌ Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
证法三:过点P 作∠APB的平分线C.
则∠1=∠2.
在△PCA 和△PCB 中,
PA =PB
∠1=∠2
PC =PC
∴ △PCA ≌ △PCB(SAS).
∴ AC =BC.∠PCA=∠PCB=90°
∴ 点P 在线段AB 的垂直平分线上.
1
2
P
A
B
C
证法四:过点P 作AB 的垂直平分线PC.
∵ AC =BC.
∠PCA=∠PCB=90°
∴ 点P 在线段AB 的垂直平分线上.
A
P
B
D
(1)
A
P
B
D
(2)
一般情况下,“过点P作AB的垂直平分线”是不可能实现的。
几何语言:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
归纳:与线段两个端点距离相等的点在这条线段的垂直平分线上
尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
直线CF就是所求作的垂线.
F
合作探究二
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交AB于点D和点E.
(3)分别以点D和点E为圆心,大于 DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.
想一想:
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 DE的长为半径作弧?
(3)为什么直线CF 就是所求作的垂线?
1.如图所示,AC=AD ,BC=BD,则下列说法正确的
是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
2.在锐角三角形ABC内一点P,满足PA=PB=PC,
则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
当堂检测
A
B
C
M
3.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
4.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
第3题图
第4题图
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
课堂小结
