人教新版九年级数学下学期 第29章 投影与视图单元复习试题(解析版)
文档属性
| 名称 | 人教新版九年级数学下学期 第29章 投影与视图单元复习试题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 350.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览



文档简介
第29章 投影与视图
一.选择题(共20小题)
1.下列说法错误的是( )
A.高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长
B.对角线互相垂直的四边形是菱形
C.方程x2=x的根是x1=0,x2=1
D.对角线相等的平行四边形是矩形
2.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
3.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长 B.逐渐变短
C.长度不变 D.先变短后变长
4.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( )
A.③①④② B.③②①④ C.③④①② D.②④①③
5.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )
A.3.2米 B.4.8米 C.5.2米 D.5.6米
6.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是( )
A. B. C. D.
7.如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越大 B.越小 C.不变 D.无法确定
8.当你乘车沿一条平坦的大道向前行驶时,你会发现,前方哪些高一些的建筑物好像“沉”到了位于它们前面哪些矮一些的建筑物后面去了.这是因为( )
A.汽车开的很快 B.盲区减小
C.盲区增大 D.无法确定
9.如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
A.逐渐变大 B.逐渐变小 C.不变 D.无法确定
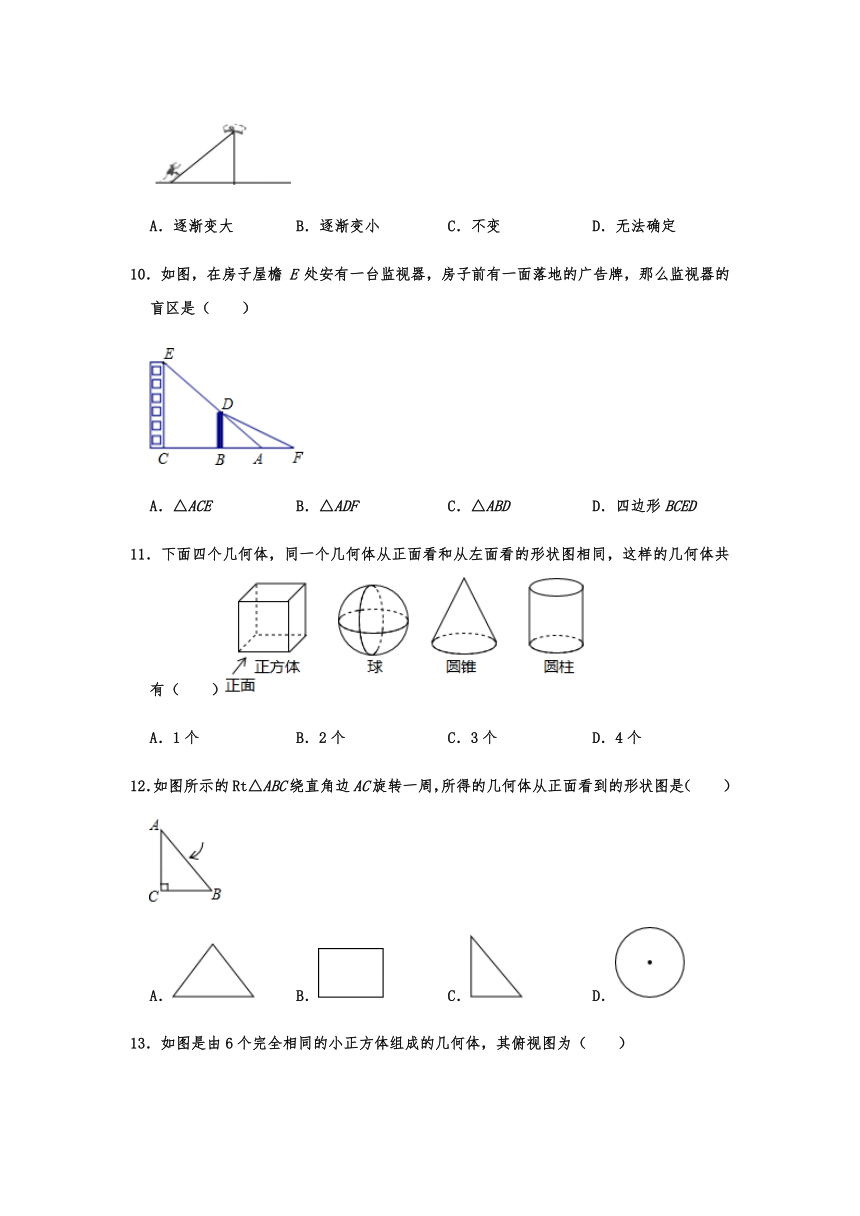
10.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A.△ACE B.△ADF C.△ABD D.四边形BCED
11.下面四个几何体,同一个几何体从正面看和从左面看的形状图相同,这样的几何体共有( )
A.1个 B.2个 C.3个 D.4个
12.如图所示的Rt△ABC绕直角边AC旋转一周,所得的几何体从正面看到的形状图是( )
A. B. C. D.
13.如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
A. B. C. D.
14.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A. B. C. D.
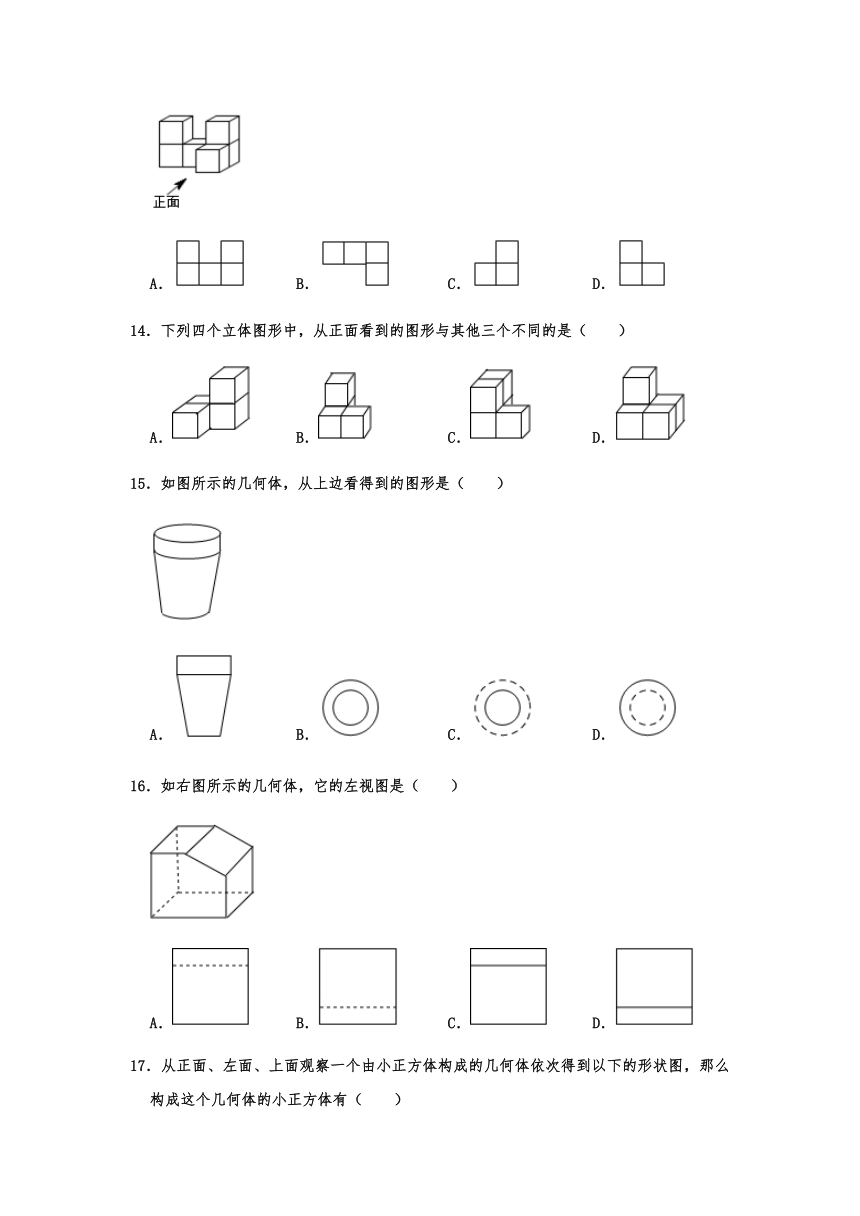
15.如图所示的几何体,从上边看得到的图形是( )
A. B. C. D.
16.如右图所示的几何体,它的左视图是( )
A. B. C. D.
17.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
18.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
19.一个几何体由大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看这个几何体得到的形状图是( )
A. B. C. D.
20.桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
A. B.
C. D.
二.填空题(共3小题)
21.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是 .
22.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 cm2.
23.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有 .
三.解答题(共6小题)
24.如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
25.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
26.李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
27.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
28.如图,是一个由小正方体所搭成的几何体,从上面看到的平面图形,从正方形中的数字表示该位置小正方体的个数,请你画出它从正面和从左面看到的平面图形.
29.一个几何体由几个大小相同的小立方块搭成,从上面看到的这个几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.
(1)请画出从正面和左面看到的这个几何体的形状图;
(2)如果保持从正面看到的和从左面看到的形状图不变.最多可以再添加 个小立方块.
参考答案与试题解析
一.选择题(共20小题)
1.下列说法错误的是( )
A.高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长
B.对角线互相垂直的四边形是菱形
C.方程x2=x的根是x1=0,x2=1
D.对角线相等的平行四边形是矩形
【分析】利用中心投影的知识、菱形的判定、一元二次方程的解及矩形的判定分别判断后即可确定正确的选项.
【解答】解:A、高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长,正确,不符合题意;
B、对角线互相垂直的平行四边形是菱形,故错误,符合题意;
C、方程x2=x的根是x1=0,x2=1,正确,不符合题意;
D、对角线相等的平行四边形是矩形,正确,不符合题意;
故选:B.
2.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
【分析】根据在平行投影中,投影线垂直于投影面产生的投影叫做正投影解答即可.
【解答】解:圆形的纸片在平行投影下的正投影可能是圆形、椭圆形、线段,
故选:D.
3.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长 B.逐渐变短
C.长度不变 D.先变短后变长
【分析】因为人和路灯间的位置发生了变化,光线与地面的夹角发生变化,所以影子的长度也会发生变化,进而得出答案.
【解答】解:当他远离路灯走向B处时,光线与地面的夹角越来越小,小明在地面上留下的影子越来越长,
所以他在走过一盏路灯的过程中,其影子的长度逐渐变长,
故选:A.
4.下面是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序正确的是( )
A.③①④② B.③②①④ C.③④①② D.②④①③
【分析】太阳光可以看做平行光线,从而可求出答案.
【解答】解:太阳从东边升起,西边落下,
所以先后顺序为:③④①②
故选:C.
5.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )
A.3.2米 B.4.8米 C.5.2米 D.5.6米
【分析】由成比例关系,列出关系式,代入数据即可求出结果.
【解答】解:设旗杆的高为x,有,可得x=4.8米.
故选:B.
6.如图所示,右面水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是( )
A. B. C. D.
【分析】根据题意:水杯的杯口与投影面平行,即与光线垂直;则它的正投影图是应是D.
【解答】解:依题意,光线是垂直照下的,故只有D符合.
故选:D.
7.如图,白炽灯下有一个乒乓球,当乒乓球越接近灯泡时,它在地面上的影子( )
A.越大 B.越小 C.不变 D.无法确定
【分析】根据中心投影的特点可知:在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以白炽灯向上移时,阴影会逐渐变小.相反当乒乓球越接近灯泡时,它在地面上的影子变大.
【解答】解:白炽灯向上移时,阴影会逐渐变小;相反当乒乓球越接近灯泡时,它在地面上的影子变大.
故选:A.
8.当你乘车沿一条平坦的大道向前行驶时,你会发现,前方哪些高一些的建筑物好像“沉”到了位于它们前面哪些矮一些的建筑物后面去了.这是因为( )
A.汽车开的很快 B.盲区减小
C.盲区增大 D.无法确定
【分析】前方哪些高一些的建筑物好像“沉”到了位于它们前面哪些矮一些的建筑物后面去了,说明看到的范围减少,即盲区增大.
【解答】解:根据题意我们很明显的可以看出“沉”下去的建筑物实际上是到了自己的盲区的范围内.
故选:C.
9.如图,一只小猴顺着一根斜放的竹竿往上爬,眼睛一直盯着挂在上端的帽子,在小猴爬行的过程中,视线与水平方向所成角( )
A.逐渐变大 B.逐渐变小 C.不变 D.无法确定
【分析】根据视线与水平方向所成角处处都是两直线平行,同位角相等.
【解答】解:∵在小猴爬行的过程中,视线与水平方向所成角等于,竹竿与地面的夹角,
∴视线与水平方向所成角不变,
故选:C.
10.如图,在房子屋檐E处安有一台监视器,房子前有一面落地的广告牌,那么监视器的盲区是( )
A.△ACE B.△ADF C.△ABD D.四边形BCED
【分析】根据盲区的定义,视线覆盖不到的地方即为该视点的盲区,由图知,E是视点,找到在E点处看不到的区域即可.
【解答】解:由图片可知,E视点的盲区应该在△ABD的区域内.
故选:C.
11.下面四个几何体,同一个几何体从正面看和从左面看的形状图相同,这样的几何体共有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据几何体的三视图解答即可.
【解答】解:正方体、球,圆锥与圆柱四种几何体从正面看和从左面看,看到的相同,
故选:D.
12.如图所示的Rt△ABC绕直角边AC旋转一周,所得的几何体从正面看到的形状图是( )
A. B. C. D.
【分析】应先得到旋转后得到的几何体,找到从正面看所得到的图形即可.
【解答】解:Rt△ABC绕直角边AC旋转一周,所得几何体是圆锥,圆锥的主视图是等腰三角形,
故选:A.
13.如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
A. B. C. D.
【分析】根据从上面看得到的图形是俯视图,据此可得答案.
【解答】解:从上面看第一排是三个小正方形,第二排右边是一个小正方形,
故选:B.
14.下列四个立体图形中,从正面看到的图形与其他三个不同的是( )
A. B. C. D.
【分析】根据图中的主视图解答即可.
【解答】解:A、的主视图是第一层两个小正方形,第二层右边一个小正方形,
B、的主视图是第一层两个小正方形,第二层左边一个小正方形,
C、的主视图是第一层两个小正方形,第二层左边一个小正方形,
D、的主视图是第一层两个小正方形,第二层左一个小正方形,
故选:A.
15.如图所示的几何体,从上边看得到的图形是( )
A. B. C. D.
【分析】从上面看,能看到的是圆形,但看不到的底面的轮廓线用虚线表示.
【解答】解:从上面看到的是圆形,相当于看一个杯子的俯视图,因此选择D,
故选:D.
16.如右图所示的几何体,它的左视图是( )
A. B. C. D.
【分析】根据从左边看得到的图形是左视图,可得答案.
【解答】解:图中所示几何体的左视图如图:
故选:A.
17.从正面、左面、上面观察一个由小正方体构成的几何体依次得到以下的形状图,那么构成这个几何体的小正方体有( )
A.4个 B.5个 C.6个 D.7个
【分析】易得这个几何体共有2层,由俯视图可得第一层正方体的个数,由主视图和左视图可得第二层正方体的个数,相加即可.
【解答】解:由从上面看到的图形易得最底层有4个正方体,第二层有1个正方体,
那么共有4+1=5(个)正方体.
故选:B.
18.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
【分析】由几何体的主视图和俯视图可知,该几何体的主视图的第一列3个正方形中每个正方形所在位置最多均可有2个小立方块;最少一个正方形所在位置有2个小立方块,其余2个所在位置各有1个小立方块;主视图的第二列1个小正方形所在位置只能有1个.再根据用6个小立方块搭一个几何体即可求解.
【解答】解:这样的几何体不止一种,而有多种摆法.
最少需要2+1+1+1=5(个)小立方块,最多需要2×3+1=7(个)小立方块.
因为用6个小立方块搭一个几何体,
所以它的左视图不可能是.
故选:D.
19.一个几何体由大小相同的小立方块搭成,从上面看到的几何体形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看这个几何体得到的形状图是( )
A. B. C. D.
【分析】从正面看,注意“长对正,宽相等、高平齐”,根据所放置的小立方体的个数画出图形即可.
【解答】解:从正面看所得到的图形为:B
故选:B.
20.桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
A. B.
C. D.
【分析】俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得左视图有3列,从左到右分别是2,3,2个正方形.
【解答】解:由俯视图中的数字可得:左视图有3列,从左到右分别是2,3,2个正方形.
故选:D.
二.填空题(共3小题)
21.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是 (4,0) .
【分析】根据相似三角形的判定和性质即可得到结论.
【解答】解:∵BC∥DE,
∴△ABC∽△ADE,
∴,
∵BC=1.2,
∴DE=2,
∴E(4,0).
故答案为:(4,0).
22.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 500 cm2.
【分析】易得对应点到对应中心的比值,那么面积比为对应点到对应中心的比值的平方,据此求解可得.
【解答】解:∵OA:OA′=2:5,
可知OB:OB′=2:5,
∵∠AOB=∠A′OB′,
∴△AOB∽△A′OB′,
∴AB:A′B′=2:5,
∴矩形ABCD的面积:矩形A′B′C′D′的面积为4:25,
又矩形ABCD的面积为80cm2,则矩形A′B′C′D′的面积为500cm2.
故答案为:500cm2.
23.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数最多有 6 .
【分析】易得这个几何体共有2层,由俯视图可得第一层小正方体的个数,由主视图可得第二层小正方体的最多个数,相加即可.
【解答】解:由俯视图易得最底层有4个小正方体,第二层最多有2个小正方体,那么搭成这个几何体的小正方体最多为4+2=6个.
故答案为:6
三.解答题(共6小题)
24.如图,AB和DE是直立在地面上的两根立柱.AB=4m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
【分析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB:DE=BC:EF.计算可得DE=10(m).
【解答】解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴AB:DE=BC:EF,
∵AB=4m,BC=3m,EF=8
∴4:3=DE:8
∴DE=(m).
25.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
【分析】利用正切的定义分别在两个直角三角形中有AB表示出BD和BC,然后利用BC﹣BD=8列方程,再解关于AB的方程即可.
【解答】解:在Rt△ABD中,∵tan∠ADB=,
∴BD==,
在Rt△ACB中,∵tan∠ACB=,
∴BC===,
∵BC﹣BD=8,
∴﹣=8,
∴AB=4(m).
答:树高AB为4米.
26.李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.
【分析】过点D作DN⊥AB,可得四边形CDME、ACDN是矩形,即可证明△DFM∽△DBN,从而得出BN,进而求得AB的长.
【解答】解:过点D作DN⊥AB,垂足为N.交EF于M点,
∴四边形CDME、ACDN是矩形,
∴AN=ME=CD=1.2m,DN=AC=30m,DM=CE=0.6m,
∴MF=EF﹣ME=1.6﹣1.2=0.4m,
∴依题意知,EF∥AB,
∴△DFM∽△DBN,
=,
即:=,
BN=20,
AB=BN+AN=20+1.2=21.2
答:楼高为21.2米.
27.在一个阳光明媚的上午,数学陈老师组织学生测量小山坡的一棵大树CD的高度,山坡OM与地面ON的夹角为30°(∠MON=30°),站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米,此刻大树CD在斜坡的影长DQ为5米,求大树的高度.
【分析】根据题意过点Q作QE⊥DC于点E,由题意可得:△ABP∽△CEQ,进而得出EQ,DE,EC的长,即可得出答案.
【解答】解:过点Q作QE⊥DC于点E,
由题意可得:△ABP∽△CEQ,
则=,故=,
可得:EQ∥NO,
则∠1=∠2=30°,
∵QD=5m,
∴DE=m,EQ=m,
故==,
解得:EC=,
故CE+DE=+=(m),
答:大树的高度为m.
28.如图,是一个由小正方体所搭成的几何体,从上面看到的平面图形,从正方形中的数字表示该位置小正方体的个数,请你画出它从正面和从左面看到的平面图形.
【分析】根据三视图的定义画出图形即可.
【解答】解:从正面和从左面看到的平面图形如图所示:
29.一个几何体由几个大小相同的小立方块搭成,从上面看到的这个几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.
(1)请画出从正面和左面看到的这个几何体的形状图;
(2)如果保持从正面看到的和从左面看到的形状图不变.最多可以再添加 8 个小立方块.
【分析】(1)直接利用俯视图中所标数字进而得出主视图以及左视图;
(2)直接利用主视图以及左视图得出最多的排列方式.
【解答】解:(1)如图所示:
;
(2)从正面看到的和从左面看到的形状图不变,最多可以再添加8个小立方块.
故答案为:8.
