人教版九年级数学下册教学讲义,复习补习资料(含知识讲解,巩固练习):62【基础】《相似》全章复习与巩固含答案
文档属性
| 名称 | 人教版九年级数学下册教学讲义,复习补习资料(含知识讲解,巩固练习):62【基础】《相似》全章复习与巩固含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 351.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览



文档简介
《相似》全章复习与巩固--知识讲解(基础)
【学习目标】
1、了解比例的基本性质,线段的比、成比例线段; 2、通过具体实例认识图形的相似,探索相似图形的性质,理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方,探索并掌握相似三角形的判定方法,并能利用这些性质和判定方法解决生活中的一些实际问题; 3、了解图形的位似,能够利用位似将一个图形放大或缩小,在同一直角坐标系中,感受位似变换后点的坐标的变化; 4、结合相似图形性质和判定方法的探索和证明,进一步培养推理能力,发展逻辑思维能力和推理论证的表达能力,以及综合运用知识的能力,运用学过的知识解决问题的能力.
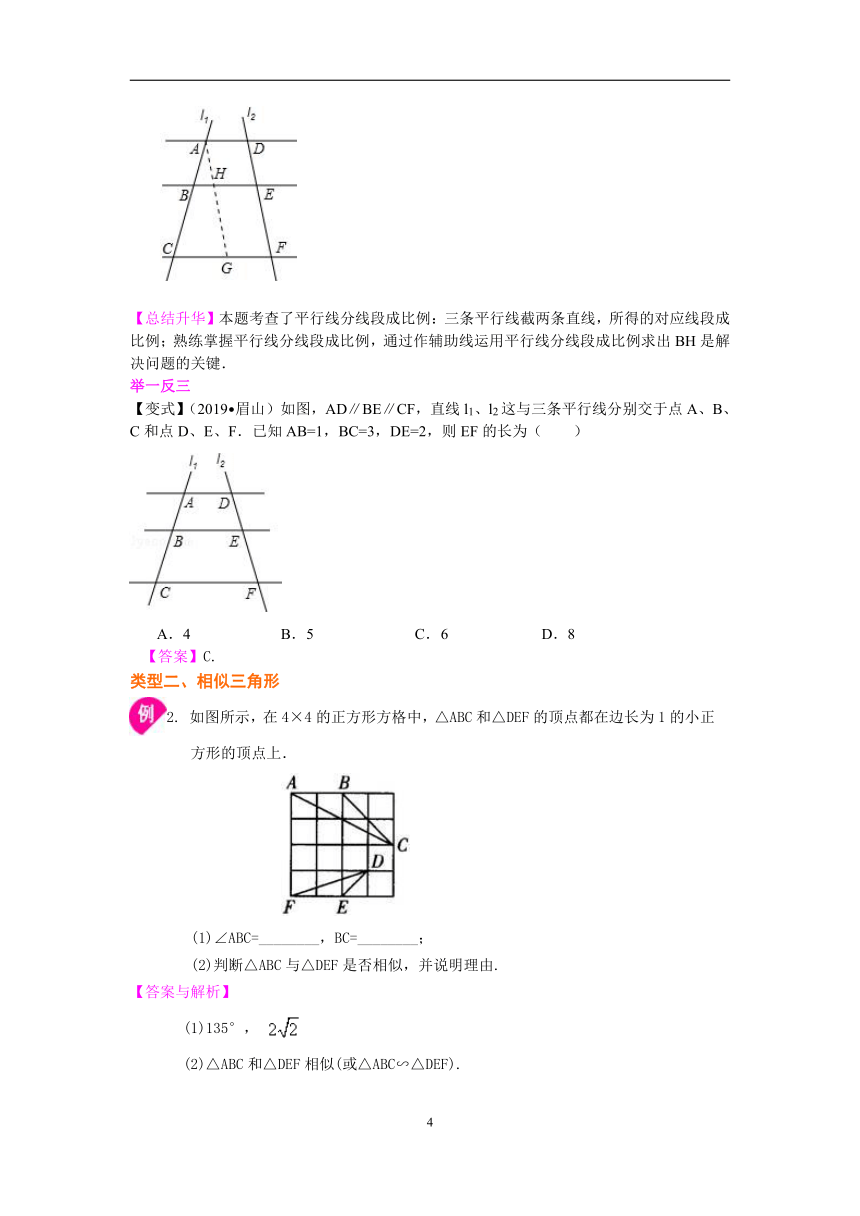
【知识网络】
【要点梳理】
要点一、相似图形及比例线段
1.相似图形:在数学上,我们把形状相同的图形称为相似图形(similar figures).
要点诠释: (1) 相似图形就是指形状相同,但大小不一定相同的图形; (2) “全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两 个图形全等;
2.相似多边形
如果两个多边形的对应角相等,对应边的比相等,我们就说它们是相似多边形.
要点诠释:
(1)相似多边形的定义既是判定方法,又是它的性质.
(2)相似多边形对应边的比称为相似比.
3. 比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.
要点诠释:
(1)若a:b=c:d ,则ad=bc;(d也叫第四比例项)
(2)若a:b=b:c ,则 =ac(b称为a、c的比例中项).
要点二、相似三角形
相似三角形的判定:
判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
要点诠释: 此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必须是两边的夹角,否则,判断的结果可能是错误的.
判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似. 要点诠释: 要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.
相似三角形的性质:
(1)相似三角形的对应角相等,对应边的比相等;
(2)相似三角形中的重要线段的比等于相似比;
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
(3) 相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方。
3.相似多边形的性质:
(1)相似多边形的对应角相等,对应边的比相等.
(2)相似多边形的周长比等于相似比.
(3)相似多边形的面积比等于相似比的平方.
要点三、位似
1.位似图形定义: 如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形的对应点和位似中心在同一条直线上; (2) 位似图形的对应点到位似中心的距离之比等于相似比; (3)位似图形中不经过位似中心的对应线段平行.
要点诠释:
(1)位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.
(2)位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
【典型例题】
类型一、相似图形及比例线段
1. (2019?崇明县一模)如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
【思路点拨】(1)由平行线分线段成比例定理和比例的性质得出,即可求出AB的长,得出BC的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,得出AD=HE=GF=7,由平行线分线段成比例定理得出比例式求出BH,即可得出结果.
【答案与解析】 解:(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,∴AB=4,
∴BC=14﹣4=10;
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
【总结升华】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键.
举一反三
【变式】(2019?眉山)如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B. 5 C. 6 D.8
【答案】C.
类型二、相似三角形
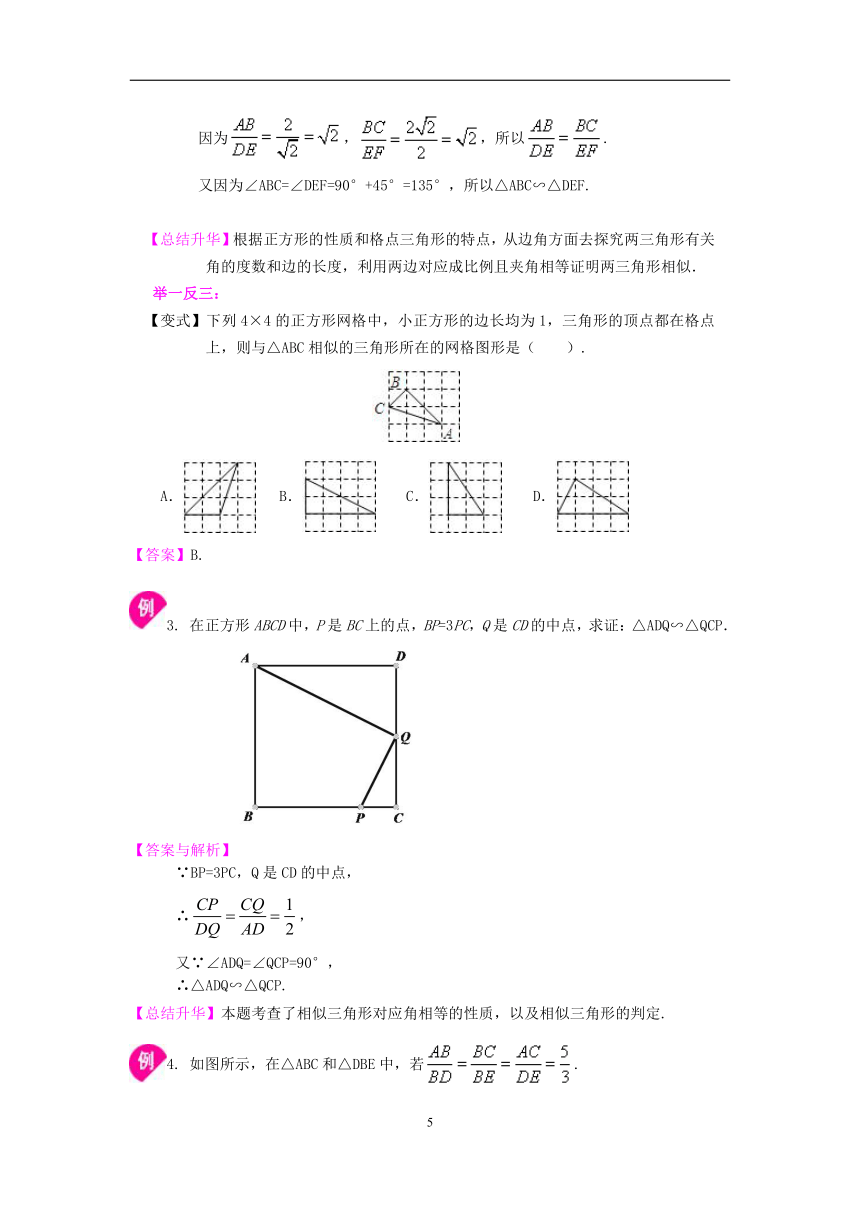
2. 如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上. (1)∠ABC=________,BC=________; (2)判断△ABC与△DEF是否相似,并说明理由.
【答案与解析】
(1)135°, (2)△ABC和△DEF相似(或△ABC∽△DEF). 因为,,所以. 又因为∠ABC=∠DEF=90°+45°=135°,所以△ABC∽△DEF.
【总结升华】根据正方形的性质和格点三角形的特点,从边角方面去探究两三角形有关角的度数和边的长度,利用两边对应成比例且夹角相等证明两三角形相似.
举一反三:
【变式】下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( ).
A. B. C. D.
【答案】B.
3. 在正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
【答案与解析】
∵BP=3PC,Q是CD的中点,
∴,
又∵∠ADQ=∠QCP=90°, ∴△ADQ∽△QCP.
【总结升华】本题考查了相似三角形对应角相等的性质,以及相似三角形的判定.
4. 如图所示,在△ABC和△DBE中,若. (1)△ABC与△DBE的周长差为10 cm,求△ABC的周长; (2)△ABC与△DBE的面积之和为170 cm2,求△DBE的面积.
【答案与解析】
(1)∵ , ∴ △ABC∽△DBE. ∴ ,设△ABC的周长为5k cm,△DBE的周长为3k cm, ∴ ,,, ∴ △ABC的周长为. (2)∵ △ABC∽△DBE,∴ . 设,. ∴ ,解得k=5, ∴ . 【总结升华】相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方.
举一反三 【变式】如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=( )
A.2:5:25 B.4:9:25 C.2:3:5 D.4:10:25
【答案】D.
5. 如图所示,已知在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=120°,设,. (1)求y与x的函数解析式; (2)当x为何值时,y有最大值?最大值是多少?
【答案与解析】
(1)在梯形ABCD中,AD∥BC, AB=DC=AD=6,∠ABC=60°,所以∠A=∠D=120°, 所以∠AEB+∠ABE=180°-120°=60°. 因为∠BEF=120°,所以∠AEB+∠DEF=180°-120°=60°, 所以∠ABE=∠DEF. 所以△ABE∽△DEF,所以. 因为,,所以, 所以y与x的函数解析式是. (2), 所以当时,y有最大值,最大值为.
【总结升华】本题考查了等腰梯形的性质,相似三角形的判定和性质,以及二次函数的最值问题.
举一反三 【变式】如图所示,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y. (1)求出y关于x的函数关系式,并写出自变量x的取值范围; (2)当x为何值时,△BDE的面积S有最大值,最大值为多少?
【答案】
(1)因为DE∥BC,所以△ADE∽△ABC, 所以. 又因为AB=8,AC=6,,, 所以,即, 自变量x的取值范围为. (2) . 所以当时,S有最大值,且最大值为6.
类型三、位似
6. 将下图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化. (1)沿y轴负方向平移1个单位; (2)关于x轴对称; (3)以C点为位似中心,放大到1.5倍.
【答案与解析】
变换后的图形如下图所示. (1)将△ABC沿y轴负方向平移1个单位后得到△A1B1C1, A1(-5,-1),B1(0,2),C1(0,-1). 即横坐标不变,纵坐标减小. (2)将△ABC关于x轴对称后,得△A2B2C2,A2(-5,0),B2(0,-3),C2(0,0). 即横坐标不变,纵坐标变为原来的相反数. (3)将△ABC以C点为位似中心,放大到1.5倍得△A3B3C3(有2个三角形), 显然,A3(-5×1.5,0),B3(0,3×1.5),C3(0,0), 即A3(-7.5,0),B3(0,4.5),C3(0,0),或A3(7.5,0)、B3(0,-4.5)、C3(0,0).
【总结升华】本题应先按图形变换的要求画出相应的图形,再求出变换后图形的点的坐标,
第(3)问可先求变换后图形的点的坐标,但注意此时的位似中心是原点.
《相似》全章复习与巩固--巩固练习(基础)
【巩固练习】
一、选择题
1.(2019?乐山)如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
2. (2019?奉贤区一模)用一个4倍放大镜照△ABC,下列说法错误的是( )
A.△ABC放大后,∠B是原来的4倍
B.△ABC放大后,边AB是原来的4倍
C.△ABC放大后,周长是原来的4倍
D.△ABC放大后,面积是原来的16倍
3.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是( )
4.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是,则点B的横坐标是( ) A. B. C. D.
5.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )
A.1个 B.2个 C.3个 D.4个
6. 如图,在正方形ABCD中,E是CD的中点,P是BC边上的点,下列条件中不能推出△ABP与以点E、C、P为顶点的三角形相似的是( ) A.∠APB=∠EPC B.∠APE=90° C.P是BC的中点 D.BP:BC=2:3 7. 如图,在△ABC中,EF∥BC,,,S四边形BCFE=8,则S△ABC=( )
A.9 B.10 C.12 D.13
8.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
A.∠E=2∠K B.BC=2HI
C.六边形ABCDEF的周长=六边形GHIJKL的周长 D.S六边形ABCDEF=2S六边形GHIJKL
二、填空题
9. (2019?衡阳)若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
10. 如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE与△ABC的面积之比为_______,△CFG与△BFD的面积之比为________.
11. 如图,梯形ABCD中,AD∥BC,AC、BD交于O点,S△AOD:S△COB=1:9,则S△DOC:S△BOC=_______.
12. 在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在
面上的影长为40米,则古塔高为________.
13. (2019?金华)如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是 .
14.如图,在△ABC中,MN∥BC,若∠C=68°,AM:MB=1:2,则∠MNA=_______度,AN:NC=_____________.
15.如图,点D,E分别在AB、AC上,且∠ABC=∠AED。若DE=4,AE=5,BC=8,则AB的长为_________.
第14题 第15题
16. -油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油面的高度为 .
三、解答题
17. 如图,等腰直角△ABC的斜边AB所在的直线上有点E、F,且∠E+∠F=45°,AE=3,设AB=x,BF=y,求y关于x的函数解析式.
18.(2019?岳阳)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
19. 如图,圆中两弦AB、CD相交于M,且AC=CM=MD,MB=AM=1,求此圆的直径的长.
20. 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6)那么: (1)当t为何值时,△QAP为等腰直角三角形? (2)对四边形QAPC的面积,提出一个与计算结果有关的结论; (3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
【答案与解析】
一.选择题
1.【答案】D. 【解析】∵l1∥l2∥l3,,
∴===,故选:D.
2.【答案】A.
【解析】∵放大前后的三角形相似,
∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍,
则A错误,符合题意.
3.【答案】A
【解析】考点:相似三角形的判定.
4.【答案】D.
5.【答案】B. 【解析】提示:①③.
6.【答案】C.
7.【答案】A.
【解析】 求出的值,推出△AEF∽△ABC,得出,把S四边形BCFE=8代入求出即可.
8.【答案】B.
【解析】根据相似多边形的性质对各选项进行逐一分析即可.
二.填空题
9.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,
∴△ABC与△DEF的相似比为5:4;
∴△ABC与△DEF的周长之比为5:4.
10.【答案】2,1:4,1:6.
11.【答案】1:3 .
【解析】∵S△AOD:S△COB=1:9,,∵△AOD与△DOC等高,∴S△AOD:S△DOC=1:3, ∴S△DOC:S△BOC=1:3.
12.【答案】30m.
13.【答案】5.
【解析】∵l3∥l6,
∴BC∥EF,
∴△ABC∽△AEF,
∴=,
∵BC=2,
∴EF=5.
14.【答案】68°,1:2.
【解析】首先,想到定理的含义,再结合图形分析(或进行比例变形)就可直接求出结果.
15.【答案】10.
【解析】∵∠ABC=∠AED,∠BAC=∠EAD∴△AED∽△ABC,∴,DE=10.
16.【答案】0.64m.
【解析】将实际问题转化为几何问题是解题的关键,即由题意可得Rt△ABC,其中AB=1m,AC=0.8m,BD=0.8m,DE//BC,将问题转化为求CE的长,由平行线分线段成比例定理计算即得.
三. 解答题
17.【解析】解:△ABC为等腰直角三角形,∠CAB=∠CBA=45°,∠E+∠F=45°, ∠E+∠ECA=∠CAB=45°,∠F+∠BCF=∠CBA=45°, 所以∠ECA=∠F,∠E=∠BCF, 所以△ECA∽△CFB,,3y=CA2=x2,即y=x2.
18.【解析】证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM==13,AD=12,
∵F是AM的中点,
∴AF=AM=6.5,
∵△ABM∽△EFA,
∴,
即,
∴AE=16.9,
∴DE=AE﹣AD=4.9.
19.【解析】连结BD,由∠CAM=∠BDM,∠AMC=∠DMB,△ACM∽△DBM,, 又DM=CM,CM2=AM·BM=2,CM=DM=,AC=. 又AC2+CM2=AM2,所以∠ACD=90°, 所以圆的直径为AD==.
20.【解析】(1)对于任何时刻t,AP=2t,DQ=t,QA=6-t, 当QA=AP时,△QAP是等腰直角三角形,即6-t=2t,t=2秒. (2) 四边形QAPC的面积=S△QAC+S△APC =(36-6t)+6t=36cm2, 在P、Q两点移动的过程中, 四边形QAPC的面积始终保持不变(或P、Q两点到对角线AC的距离之和保持不变) (3)分两种情况: ①当时△QAP∽△ABC,则,从而t=1.2, ②当时△PAQ∽△ABC,则,从而t=3.
【学习目标】
1、了解比例的基本性质,线段的比、成比例线段; 2、通过具体实例认识图形的相似,探索相似图形的性质,理解相似多边形对应角相等、对应边成比例、周长的比等于相似比、面积的比等于相似比的平方,探索并掌握相似三角形的判定方法,并能利用这些性质和判定方法解决生活中的一些实际问题; 3、了解图形的位似,能够利用位似将一个图形放大或缩小,在同一直角坐标系中,感受位似变换后点的坐标的变化; 4、结合相似图形性质和判定方法的探索和证明,进一步培养推理能力,发展逻辑思维能力和推理论证的表达能力,以及综合运用知识的能力,运用学过的知识解决问题的能力.
【知识网络】
【要点梳理】
要点一、相似图形及比例线段
1.相似图形:在数学上,我们把形状相同的图形称为相似图形(similar figures).
要点诠释: (1) 相似图形就是指形状相同,但大小不一定相同的图形; (2) “全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两 个图形全等;
2.相似多边形
如果两个多边形的对应角相等,对应边的比相等,我们就说它们是相似多边形.
要点诠释:
(1)相似多边形的定义既是判定方法,又是它的性质.
(2)相似多边形对应边的比称为相似比.
3. 比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.
要点诠释:
(1)若a:b=c:d ,则ad=bc;(d也叫第四比例项)
(2)若a:b=b:c ,则 =ac(b称为a、c的比例中项).
要点二、相似三角形
相似三角形的判定:
判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
要点诠释: 此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必须是两边的夹角,否则,判断的结果可能是错误的.
判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似. 要点诠释: 要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似.
相似三角形的性质:
(1)相似三角形的对应角相等,对应边的比相等;
(2)相似三角形中的重要线段的比等于相似比;
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
(3) 相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方。
3.相似多边形的性质:
(1)相似多边形的对应角相等,对应边的比相等.
(2)相似多边形的周长比等于相似比.
(3)相似多边形的面积比等于相似比的平方.
要点三、位似
1.位似图形定义: 如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
2.位似图形的性质:
(1)位似图形的对应点和位似中心在同一条直线上; (2) 位似图形的对应点到位似中心的距离之比等于相似比; (3)位似图形中不经过位似中心的对应线段平行.
要点诠释:
(1)位似图形与相似图形的区别:位似图形是一种特殊的相似图形,而相似图形未必能构成位似图形.
(2)位似变换中对应点的坐标变化规律:在平面直角坐标系中,如果位似变换是以原点
为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
【典型例题】
类型一、相似图形及比例线段
1. (2019?崇明县一模)如图,已知AD∥BE∥CF,它们依次交直线l1、l2于点A、B、C和点D、E、F,,AC=14;
(1)求AB、BC的长;
(2)如果AD=7,CF=14,求BE的长.
【思路点拨】(1)由平行线分线段成比例定理和比例的性质得出,即可求出AB的长,得出BC的长;
(2)过点A作AG∥DF交BE于点H,交CF于点G,得出AD=HE=GF=7,由平行线分线段成比例定理得出比例式求出BH,即可得出结果.
【答案与解析】 解:(1)∵AD∥BE∥CF,
∴,
∴,
∵AC=14,∴AB=4,
∴BC=14﹣4=10;
(2)过点A作AG∥DF交BE于点H,交CF于点G,如图所示:
又∵AD∥BE∥CF,AD=7,
∴AD=HE=GF=7,
∵CF=14,
∴CG=14﹣7=7,
∵BE∥CF,
∴,
∴BH=2,
∴BE=2+7=9.
【总结升华】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键.
举一反三
【变式】(2019?眉山)如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B. 5 C. 6 D.8
【答案】C.
类型二、相似三角形
2. 如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上. (1)∠ABC=________,BC=________; (2)判断△ABC与△DEF是否相似,并说明理由.
【答案与解析】
(1)135°, (2)△ABC和△DEF相似(或△ABC∽△DEF). 因为,,所以. 又因为∠ABC=∠DEF=90°+45°=135°,所以△ABC∽△DEF.
【总结升华】根据正方形的性质和格点三角形的特点,从边角方面去探究两三角形有关角的度数和边的长度,利用两边对应成比例且夹角相等证明两三角形相似.
举一反三:
【变式】下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( ).
A. B. C. D.
【答案】B.
3. 在正方形ABCD中,P是BC上的点,BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
【答案与解析】
∵BP=3PC,Q是CD的中点,
∴,
又∵∠ADQ=∠QCP=90°, ∴△ADQ∽△QCP.
【总结升华】本题考查了相似三角形对应角相等的性质,以及相似三角形的判定.
4. 如图所示,在△ABC和△DBE中,若. (1)△ABC与△DBE的周长差为10 cm,求△ABC的周长; (2)△ABC与△DBE的面积之和为170 cm2,求△DBE的面积.
【答案与解析】
(1)∵ , ∴ △ABC∽△DBE. ∴ ,设△ABC的周长为5k cm,△DBE的周长为3k cm, ∴ ,,, ∴ △ABC的周长为. (2)∵ △ABC∽△DBE,∴ . 设,. ∴ ,解得k=5, ∴ . 【总结升华】相似三角形的周长比等于相似比,相似三角形的面积比等于相似比的平方.
举一反三 【变式】如图,在平行四边形ABCD中,E是CD上的一点,DE:EC=2:3,连接AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF=( )
A.2:5:25 B.4:9:25 C.2:3:5 D.4:10:25
【答案】D.
5. 如图所示,已知在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=120°,设,. (1)求y与x的函数解析式; (2)当x为何值时,y有最大值?最大值是多少?
【答案与解析】
(1)在梯形ABCD中,AD∥BC, AB=DC=AD=6,∠ABC=60°,所以∠A=∠D=120°, 所以∠AEB+∠ABE=180°-120°=60°. 因为∠BEF=120°,所以∠AEB+∠DEF=180°-120°=60°, 所以∠ABE=∠DEF. 所以△ABE∽△DEF,所以. 因为,,所以, 所以y与x的函数解析式是. (2), 所以当时,y有最大值,最大值为.
【总结升华】本题考查了等腰梯形的性质,相似三角形的判定和性质,以及二次函数的最值问题.
举一反三 【变式】如图所示,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y. (1)求出y关于x的函数关系式,并写出自变量x的取值范围; (2)当x为何值时,△BDE的面积S有最大值,最大值为多少?
【答案】
(1)因为DE∥BC,所以△ADE∽△ABC, 所以. 又因为AB=8,AC=6,,, 所以,即, 自变量x的取值范围为. (2) . 所以当时,S有最大值,且最大值为6.
类型三、位似
6. 将下图中的△ABC作下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化. (1)沿y轴负方向平移1个单位; (2)关于x轴对称; (3)以C点为位似中心,放大到1.5倍.
【答案与解析】
变换后的图形如下图所示. (1)将△ABC沿y轴负方向平移1个单位后得到△A1B1C1, A1(-5,-1),B1(0,2),C1(0,-1). 即横坐标不变,纵坐标减小. (2)将△ABC关于x轴对称后,得△A2B2C2,A2(-5,0),B2(0,-3),C2(0,0). 即横坐标不变,纵坐标变为原来的相反数. (3)将△ABC以C点为位似中心,放大到1.5倍得△A3B3C3(有2个三角形), 显然,A3(-5×1.5,0),B3(0,3×1.5),C3(0,0), 即A3(-7.5,0),B3(0,4.5),C3(0,0),或A3(7.5,0)、B3(0,-4.5)、C3(0,0).
【总结升华】本题应先按图形变换的要求画出相应的图形,再求出变换后图形的点的坐标,
第(3)问可先求变换后图形的点的坐标,但注意此时的位似中心是原点.
《相似》全章复习与巩固--巩固练习(基础)
【巩固练习】
一、选择题
1.(2019?乐山)如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
2. (2019?奉贤区一模)用一个4倍放大镜照△ABC,下列说法错误的是( )
A.△ABC放大后,∠B是原来的4倍
B.△ABC放大后,边AB是原来的4倍
C.△ABC放大后,周长是原来的4倍
D.△ABC放大后,面积是原来的16倍
3.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是( )
4.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是,则点B的横坐标是( ) A. B. C. D.
5.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )
A.1个 B.2个 C.3个 D.4个
6. 如图,在正方形ABCD中,E是CD的中点,P是BC边上的点,下列条件中不能推出△ABP与以点E、C、P为顶点的三角形相似的是( ) A.∠APB=∠EPC B.∠APE=90° C.P是BC的中点 D.BP:BC=2:3 7. 如图,在△ABC中,EF∥BC,,,S四边形BCFE=8,则S△ABC=( )
A.9 B.10 C.12 D.13
8.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是( )
A.∠E=2∠K B.BC=2HI
C.六边形ABCDEF的周长=六边形GHIJKL的周长 D.S六边形ABCDEF=2S六边形GHIJKL
二、填空题
9. (2019?衡阳)若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
10. 如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE与△ABC的面积之比为_______,△CFG与△BFD的面积之比为________.
11. 如图,梯形ABCD中,AD∥BC,AC、BD交于O点,S△AOD:S△COB=1:9,则S△DOC:S△BOC=_______.
12. 在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在
面上的影长为40米,则古塔高为________.
13. (2019?金华)如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是 .
14.如图,在△ABC中,MN∥BC,若∠C=68°,AM:MB=1:2,则∠MNA=_______度,AN:NC=_____________.
15.如图,点D,E分别在AB、AC上,且∠ABC=∠AED。若DE=4,AE=5,BC=8,则AB的长为_________.
第14题 第15题
16. -油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油面的高度为 .
三、解答题
17. 如图,等腰直角△ABC的斜边AB所在的直线上有点E、F,且∠E+∠F=45°,AE=3,设AB=x,BF=y,求y关于x的函数解析式.
18.(2019?岳阳)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
19. 如图,圆中两弦AB、CD相交于M,且AC=CM=MD,MB=AM=1,求此圆的直径的长.
20. 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向A以1cm/s的速度移动.如果P、Q同时出发,用t秒表示移动的时间(0≤t≤6)那么: (1)当t为何值时,△QAP为等腰直角三角形? (2)对四边形QAPC的面积,提出一个与计算结果有关的结论; (3)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
【答案与解析】
一.选择题
1.【答案】D. 【解析】∵l1∥l2∥l3,,
∴===,故选:D.
2.【答案】A.
【解析】∵放大前后的三角形相似,
∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍,
则A错误,符合题意.
3.【答案】A
【解析】考点:相似三角形的判定.
4.【答案】D.
5.【答案】B. 【解析】提示:①③.
6.【答案】C.
7.【答案】A.
【解析】 求出的值,推出△AEF∽△ABC,得出,把S四边形BCFE=8代入求出即可.
8.【答案】B.
【解析】根据相似多边形的性质对各选项进行逐一分析即可.
二.填空题
9.【答案】5:4.
【解析】∵△ABC与△DEF相似且面积之比为25:16,
∴△ABC与△DEF的相似比为5:4;
∴△ABC与△DEF的周长之比为5:4.
10.【答案】2,1:4,1:6.
11.【答案】1:3 .
【解析】∵S△AOD:S△COB=1:9,,∵△AOD与△DOC等高,∴S△AOD:S△DOC=1:3, ∴S△DOC:S△BOC=1:3.
12.【答案】30m.
13.【答案】5.
【解析】∵l3∥l6,
∴BC∥EF,
∴△ABC∽△AEF,
∴=,
∵BC=2,
∴EF=5.
14.【答案】68°,1:2.
【解析】首先,想到定理的含义,再结合图形分析(或进行比例变形)就可直接求出结果.
15.【答案】10.
【解析】∵∠ABC=∠AED,∠BAC=∠EAD∴△AED∽△ABC,∴,DE=10.
16.【答案】0.64m.
【解析】将实际问题转化为几何问题是解题的关键,即由题意可得Rt△ABC,其中AB=1m,AC=0.8m,BD=0.8m,DE//BC,将问题转化为求CE的长,由平行线分线段成比例定理计算即得.
三. 解答题
17.【解析】解:△ABC为等腰直角三角形,∠CAB=∠CBA=45°,∠E+∠F=45°, ∠E+∠ECA=∠CAB=45°,∠F+∠BCF=∠CBA=45°, 所以∠ECA=∠F,∠E=∠BCF, 所以△ECA∽△CFB,,3y=CA2=x2,即y=x2.
18.【解析】证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,
∴AM==13,AD=12,
∵F是AM的中点,
∴AF=AM=6.5,
∵△ABM∽△EFA,
∴,
即,
∴AE=16.9,
∴DE=AE﹣AD=4.9.
19.【解析】连结BD,由∠CAM=∠BDM,∠AMC=∠DMB,△ACM∽△DBM,, 又DM=CM,CM2=AM·BM=2,CM=DM=,AC=. 又AC2+CM2=AM2,所以∠ACD=90°, 所以圆的直径为AD==.
20.【解析】(1)对于任何时刻t,AP=2t,DQ=t,QA=6-t, 当QA=AP时,△QAP是等腰直角三角形,即6-t=2t,t=2秒. (2) 四边形QAPC的面积=S△QAC+S△APC =(36-6t)+6t=36cm2, 在P、Q两点移动的过程中, 四边形QAPC的面积始终保持不变(或P、Q两点到对角线AC的距离之和保持不变) (3)分两种情况: ①当时△QAP∽△ABC,则,从而t=1.2, ②当时△PAQ∽△ABC,则,从而t=3.
