人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):57【基础】相似三角形的判定(附答案)
文档属性
| 名称 | 人教版九年级数学教学讲义,复习补习资料(含知识讲解,巩固练习):57【基础】相似三角形的判定(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 153.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 21:26:55 | ||
图片预览




文档简介
相似三角形的判定--知识讲解(基础)
【学习目标】
1、了解相似三角形的概念, 掌握相似三角形的表示方法及判定方法;
2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.
【要点梳理】
要点一、相似三角形
在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.
要点诠释: (1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;
(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.
要点二、相似三角形的判定定理
1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
要点诠释: 此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.
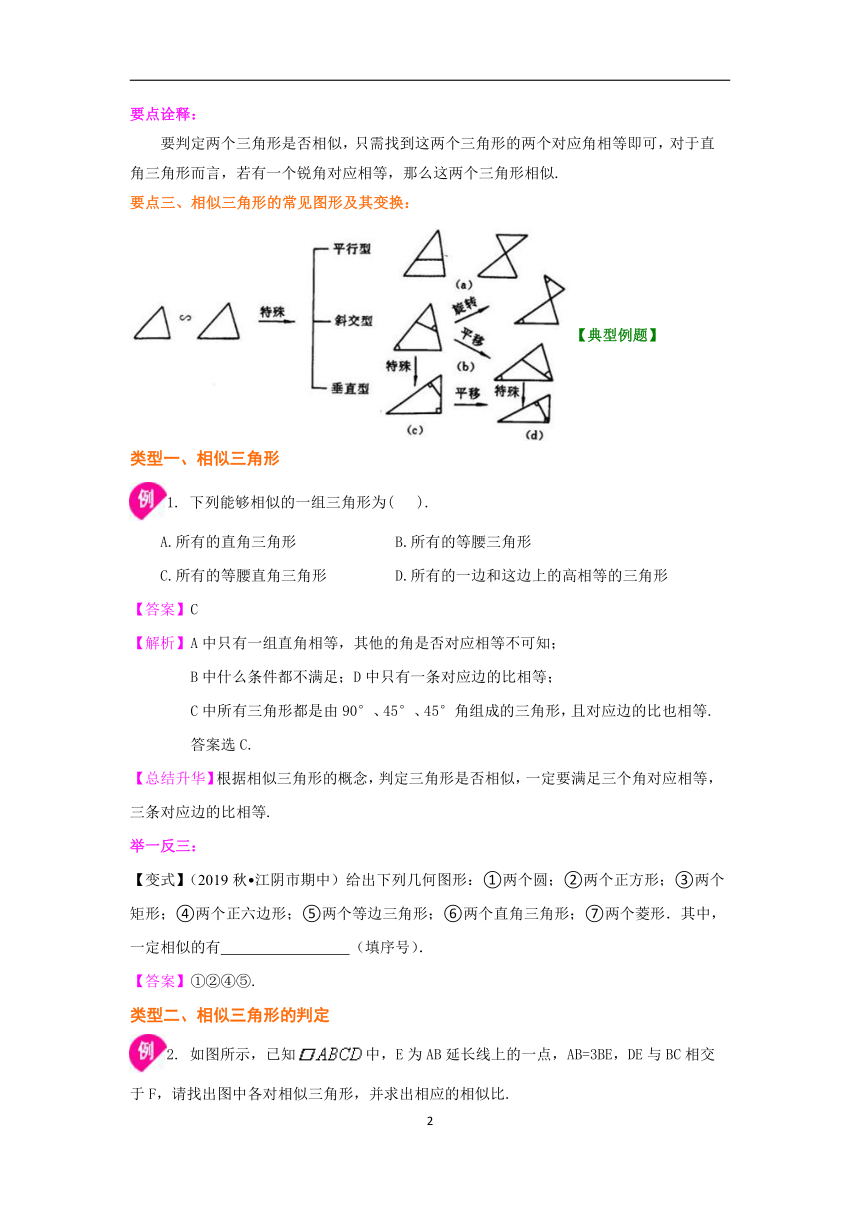
4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似. 要点诠释: 要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似. 要点三、相似三角形的常见图形及其变换:
【典型例题】
类型一、相似三角形
1. 下列能够相似的一组三角形为( ). A.所有的直角三角形 B.所有的等腰三角形 C.所有的等腰直角三角形 D.所有的一边和这边上的高相等的三角形
【答案】C
【解析】A中只有一组直角相等,其他的角是否对应相等不可知;
B中什么条件都不满足;D中只有一条对应边的比相等;
C中所有三角形都是由90°、45°、45°角组成的三角形,且对应边的比也相等.
答案选C.
【总结升华】根据相似三角形的概念,判定三角形是否相似,一定要满足三个角对应相等,三条对应边的比相等.
举一反三:
【变式】(2019秋?江阴市期中)给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有 (填序号).
【答案】①②④⑤. 类型二、相似三角形的判定
2. 如图所示,已知中,E为AB延长线上的一点,AB=3BE,DE与BC相交于F,请找出图中各对相似三角形,并求出相应的相似比. 【思路点拨】充分利用平行寻找等角,以确定相似三角形的个数.
【答案与解析】∵ 四边形ABCD是平行四边形, ∴ AB∥CD,AD∥BC, ∴ △BEF∽△CDF,△BEF∽△AED. ∴ △BEF∽△CDF∽△AED. ∴ 当△BEF∽△CDF时,相似比;
当△BEF∽△AED时,相似比; 当△CDF∽△AED时,相似比.
【总结升华】此题考查了相似三角形的判定(有两角对应相等的两三角形相似)与性质(相似三角形的对应边成比例).解题的关键是要仔细识图,灵活应用数形结合思想.
举一反三:
【变式】 如图,AD、CE是△ABC的高,AD和CE相交于点F,求证:AF·FD=CF·FE.
【答案】∵ AD、CE是△ABC的高,
∴∠AEF=∠CDF=90°,
又∵∠AFE=∠CFE,
∴△AEF∽△CDF.
∴, 即AF·FD=CF·FE.
3. (2019?福州)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求∠ABD的度数.
【思路点拨】
(1)先求得AD、CD的长,然后再计算出AD2与AC?CD的值,从而可得到AD2与AC?CD的关系;
(2)由(1)可得到BD2=AC?CD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.
【答案与解析】
解:(1)∵AD=BC=1,BC=,
∴AD=,DC=1﹣=.
∴AD2==,AC?CD=1×=.
∴AD2=AC?CD.
(2)∵AD=BC,AD2=AC?CD,
∴BC2=AC?CD,即.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.
4. 已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
【思路点拨】从求证可以判断是运用相似,再根据BP2=PE·PF,可以判定所给的线段不能组成相似三角形,这就需要考虑线段的等量转移了.
【答案与解析】连接, ,, 是的中垂线,, ,, . , . 又, ∽, , .
【总结升华】根据求证确定相似三角形,是解决此类题型的捷径.
举一反三: 【变式】如图,F是△ABC的AC边上一点,D为CB延长线一点,且AF=BD,连接DF, 交AB于E. 求证:.
【答案】过点F作FG∥BC,交AB于G.
则△DBE∽△FGE
△AGF∽△ABC
∵,
又∵AF=BD,
∴
∵△AGF∽△ABC
∴,
即.
相似三角形的判定--巩固练习(基础)
【巩固练习】
一、选择题 1. 下列判断中正确的是( ). A.全等三角形不一定是相似三角形 B.不全等的三角形一定不是相似三角形 C.不相似的三角形一定不全等 D.相似三角形一定不是全等三角形
2.已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ). A.? B.? C.?? D.?
3.(2019?大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A. ?B. ?C. D.
4. (2019?盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个
5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( ). A.ΔADE∽ΔAEF? B.ΔECF∽ΔAEF? ?C.ΔADE∽ΔECF? D.ΔAEF∽ΔABF
6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ). A.? B.8 C.10 D.16
二、填空题 7. (2019?娄底)如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.
9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).
10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.
11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.
12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.
三.解答题
13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.
14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.
15.(2019秋?射阳县校级月考)如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
(1)求证:AC2=CE?CF;
(2)若∠B=38°,求∠CFD的度数.
【答案与解析】
一.选择题
1.【答案】C.
2.【答案】A.
【解析】根据三边对应成比例,可以确定,所以第三边是
3.【答案】B.
【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.故选B.
4.【答案】C.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴△AEF∽△CBF,△AEF∽△DEC,
∴与△AEF相似的三角形有2个.
5.【答案】C.
【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°, 即∠1=∠3,∴△ADE∽△ECF.
6.【答案】C.
【解析】∵ EF∥AB,∴?, ∵?,∴?,, ∴ CD=10,故选C.
二. 填空题
7.【答案】AB∥DE.
【解析】∵∠A=∠D,
∴当∠B=∠DEF时,△ABC∽△DEF,
∵AB∥DE时,∠B=∠DEF,
∴添加AB∥DE时,使△ABC∽△DEF.
8.【答案】?3 .
【解析】∵ ∠C=∠E,∠CAB=∠EAD,∴ △ACB∽△AED, ∴?,BC=4, 在Rt△ABC中,.
9.【答案】;?.
10.【答案】4.
【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,
∴∠BCA=∠E,∴△ABC∽△CDE.
∵C是线段BD的中点,ED=1,BD=4
∴BC=CD=2
∴,即AB=4.
11.【答案】△OAB,△OCD.
12.【答案】3.
【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD
∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.
三 综合题
13.【解析】∵DE∥BC,∴△ADE∽△ABC, ∵,,∴,∴AC=,∴EC=AC-AE=.
14.【解析】∵AD∥BC,∴∠ADB=∠DBC, 又∵,∴△ABD∽△DCB, ∴∠A=∠BDC,
∵∠A=90°,∴∠BDC=90°,∴BD⊥CD?.
15.【解析】解:(1)∵AD⊥BC,
∴∠CFA=90°,
∵∠BAC=90°,
∴∠CFA=∠BAC,
∵∠ACF=∠FCA,
∴△CAF∽△CEA,
∴=,
∴CA2=CE?CF;
(2)∵∠CAB=∠CDA,∠ACD=∠BCA,
∴△CAD∽△CBA,
∴=,
∴CA2=CB×CD,
同理可得:CA2=CF×CE,
∴CD?BC=CF?CE,
∴=,
∵∠DCF=∠ECB,
∴△CDF∽△CEB,
∴∠CFD=∠B,
∵∠B=38°,
∴∠CFD=38°.
【学习目标】
1、了解相似三角形的概念, 掌握相似三角形的表示方法及判定方法;
2、进一步探索相似三角形的判定及其应用,提高运用“类比”思想的自觉性,提高推理能力.
【要点梳理】
要点一、相似三角形
在和中,如果我们就说与相似,记作∽.k就是它们的相似比,“∽”读作“相似于”.
要点诠释: (1)书写两个三角形相似时,要注意对应点的位置要一致,即∽,则说明点A的对应点是A′,点B的对应点是B′,点C的对应点是C′;
(2)对于相似比,要注意顺序和对应的问题,如果两个三角形相似,那么第一个三角形的一边和第二个三角形的对应边的比叫做第一个三角形和第二个三角形的相似比.当相似比为1时,两个三角形全等.
要点二、相似三角形的判定定理
1.判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
2.判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
3.判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
要点诠释: 此方法要求用三角形的两边及其夹角来判定两个三角形相似,应用时必须注意这个角必需是两边的夹角,否则,判断的结果可能是错误的.
4.判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似. 要点诠释: 要判定两个三角形是否相似,只需找到这两个三角形的两个对应角相等即可,对于直角三角形而言,若有一个锐角对应相等,那么这两个三角形相似. 要点三、相似三角形的常见图形及其变换:
【典型例题】
类型一、相似三角形
1. 下列能够相似的一组三角形为( ). A.所有的直角三角形 B.所有的等腰三角形 C.所有的等腰直角三角形 D.所有的一边和这边上的高相等的三角形
【答案】C
【解析】A中只有一组直角相等,其他的角是否对应相等不可知;
B中什么条件都不满足;D中只有一条对应边的比相等;
C中所有三角形都是由90°、45°、45°角组成的三角形,且对应边的比也相等.
答案选C.
【总结升华】根据相似三角形的概念,判定三角形是否相似,一定要满足三个角对应相等,三条对应边的比相等.
举一反三:
【变式】(2019秋?江阴市期中)给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有 (填序号).
【答案】①②④⑤. 类型二、相似三角形的判定
2. 如图所示,已知中,E为AB延长线上的一点,AB=3BE,DE与BC相交于F,请找出图中各对相似三角形,并求出相应的相似比. 【思路点拨】充分利用平行寻找等角,以确定相似三角形的个数.
【答案与解析】∵ 四边形ABCD是平行四边形, ∴ AB∥CD,AD∥BC, ∴ △BEF∽△CDF,△BEF∽△AED. ∴ △BEF∽△CDF∽△AED. ∴ 当△BEF∽△CDF时,相似比;
当△BEF∽△AED时,相似比; 当△CDF∽△AED时,相似比.
【总结升华】此题考查了相似三角形的判定(有两角对应相等的两三角形相似)与性质(相似三角形的对应边成比例).解题的关键是要仔细识图,灵活应用数形结合思想.
举一反三:
【变式】 如图,AD、CE是△ABC的高,AD和CE相交于点F,求证:AF·FD=CF·FE.
【答案】∵ AD、CE是△ABC的高,
∴∠AEF=∠CDF=90°,
又∵∠AFE=∠CFE,
∴△AEF∽△CDF.
∴, 即AF·FD=CF·FE.
3. (2019?福州)如图,在△ABC中,AB=AC=1,BC=,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与AC?CD的大小关系;
(2)求∠ABD的度数.
【思路点拨】
(1)先求得AD、CD的长,然后再计算出AD2与AC?CD的值,从而可得到AD2与AC?CD的关系;
(2)由(1)可得到BD2=AC?CD,然后依据对应边成比例且夹角相等的两三角形相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后结合等腰三角形的性质和三角形的内角和定理可求得∠ABD的度数.
【答案与解析】
解:(1)∵AD=BC=1,BC=,
∴AD=,DC=1﹣=.
∴AD2==,AC?CD=1×=.
∴AD2=AC?CD.
(2)∵AD=BC,AD2=AC?CD,
∴BC2=AC?CD,即.
又∵∠C=∠C,
∴△BCD∽△ACB.
∴,∠DBC=∠A.
∴DB=CB=AD.
∴∠A=∠ABD,∠C=∠BDC.
设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x.
∵∠A+∠ABC+∠C=180°,
∴x+2x+2x=180°.
解得:x=36°.
∴∠ABD=36°.
【总结升华】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角形内角和定理的应用,证得△BCD∽△ABC是解题的关键.
4. 已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F.求证:BP2=PE·PF.
【思路点拨】从求证可以判断是运用相似,再根据BP2=PE·PF,可以判定所给的线段不能组成相似三角形,这就需要考虑线段的等量转移了.
【答案与解析】连接, ,, 是的中垂线,, ,, . , . 又, ∽, , .
【总结升华】根据求证确定相似三角形,是解决此类题型的捷径.
举一反三: 【变式】如图,F是△ABC的AC边上一点,D为CB延长线一点,且AF=BD,连接DF, 交AB于E. 求证:.
【答案】过点F作FG∥BC,交AB于G.
则△DBE∽△FGE
△AGF∽△ABC
∵,
又∵AF=BD,
∴
∵△AGF∽△ABC
∴,
即.
相似三角形的判定--巩固练习(基础)
【巩固练习】
一、选择题 1. 下列判断中正确的是( ). A.全等三角形不一定是相似三角形 B.不全等的三角形一定不是相似三角形 C.不相似的三角形一定不全等 D.相似三角形一定不是全等三角形
2.已知△ABC的三边长分别为、、 2, △A′B′C′的两边长分别是1和, 如果△ABC与△A′B′C′ 相似, 那么△A′B′C′ 的第三边长应该是 ( ). A.? B.? C.?? D.?
3.(2019?大庆校级模拟)如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A. ?B. ?C. D.
4. (2019?盐城)如图,点F在平行四边形ABCD的边AB上,射线CF交DA的延长线于点E,在不添加辅助线的情况下,与△AEF相似的三角形有( )
A.0个 B.1个 C.2个 D.3个
5.在矩形ABCD中,E、F分别是CD、BC上的点,若∠AEF=90°,则一定有( ). A.ΔADE∽ΔAEF? B.ΔECF∽ΔAEF? ?C.ΔADE∽ΔECF? D.ΔAEF∽ΔABF
6. 如图所示在平行四边形ABCD中,EF∥AB,DE:EA=2:3,EF=4,则CD的长为( ). A.? B.8 C.10 D.16
二、填空题 7. (2019?娄底)如图,已知∠A=∠D,要使△ABC∽△DEF,还需添加一个条件,你添加的条件是 .(只需写一个条件,不添加辅助线和字母)
8如图所示,∠C=∠E=90°,AD=10,DE=8,AB=5,则AC=________.
9.如图所示,在直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与A不重合),当点C的坐标为________或________时,使得由点B、O、C组成的三角形与△AOB相似(至少找出两个满足条件的点的坐标).
10.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.
11.如图,CD∥AB,AC、BD相交于点O,点E、F分别在AC、BD上,且EF∥AB,则图中与△OEF相似的三角形为_________.
12.如图,点E是平行四边形ABCD的边BC延长线上一点,连接AE交CD于点F,则图中相似三角形共有_________对.
三.解答题
13. 如图,在△ABC中,DE∥BC,AD=3,AE=2,BD=4,求的值及AC、EC的长度.
14. 如图在梯形ABCD中,AD∥BC,∠A=90°,且,求证:BD⊥CD.
15.(2019秋?射阳县校级月考)如图,在△ABC中,已知∠BAC=90°,AD⊥BC于D,E是AB上一点,AF⊥CE于F,AD交CE于G点,
(1)求证:AC2=CE?CF;
(2)若∠B=38°,求∠CFD的度数.
【答案与解析】
一.选择题
1.【答案】C.
2.【答案】A.
【解析】根据三边对应成比例,可以确定,所以第三边是
3.【答案】B.
【解析】已知给出的三角形的各边AB、CB、AC分别为、2、、
只有选项B的各边为1、、与它的各边对应成比例.故选B.
4.【答案】C.
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥DC,
∴△AEF∽△CBF,△AEF∽△DEC,
∴与△AEF相似的三角形有2个.
5.【答案】C.
【解析】∵∠AEF=90°, ∴∠1+∠2=90°,又∵∠D=∠C=90°,∴∠3+∠2=90°, 即∠1=∠3,∴△ADE∽△ECF.
6.【答案】C.
【解析】∵ EF∥AB,∴?, ∵?,∴?,, ∴ CD=10,故选C.
二. 填空题
7.【答案】AB∥DE.
【解析】∵∠A=∠D,
∴当∠B=∠DEF时,△ABC∽△DEF,
∵AB∥DE时,∠B=∠DEF,
∴添加AB∥DE时,使△ABC∽△DEF.
8.【答案】?3 .
【解析】∵ ∠C=∠E,∠CAB=∠EAD,∴ △ACB∽△AED, ∴?,BC=4, 在Rt△ABC中,.
9.【答案】;?.
10.【答案】4.
【解析】∵AB⊥BD,ED⊥BD,∴∠B=∠D=90°,又∵AC⊥CE,∴∠BCA+∠DCE=90°,
∴∠BCA=∠E,∴△ABC∽△CDE.
∵C是线段BD的中点,ED=1,BD=4
∴BC=CD=2
∴,即AB=4.
11.【答案】△OAB,△OCD.
12.【答案】3.
【解析】∵平行四边形ABCD,∴AD∥BE.AB∥CD
∴△EFC∽△EAB; △EFC∽△AFD; △AFD∽△EAB.
三 综合题
13.【解析】∵DE∥BC,∴△ADE∽△ABC, ∵,,∴,∴AC=,∴EC=AC-AE=.
14.【解析】∵AD∥BC,∴∠ADB=∠DBC, 又∵,∴△ABD∽△DCB, ∴∠A=∠BDC,
∵∠A=90°,∴∠BDC=90°,∴BD⊥CD?.
15.【解析】解:(1)∵AD⊥BC,
∴∠CFA=90°,
∵∠BAC=90°,
∴∠CFA=∠BAC,
∵∠ACF=∠FCA,
∴△CAF∽△CEA,
∴=,
∴CA2=CE?CF;
(2)∵∠CAB=∠CDA,∠ACD=∠BCA,
∴△CAD∽△CBA,
∴=,
∴CA2=CB×CD,
同理可得:CA2=CF×CE,
∴CD?BC=CF?CE,
∴=,
∵∠DCF=∠ECB,
∴△CDF∽△CEB,
∴∠CFD=∠B,
∵∠B=38°,
∴∠CFD=38°.
