人教版九年级数学下册教学讲义,复习补习资料(含知识讲解,巩固练习):56【基础】图形的相似与比例线段含答案
文档属性
| 名称 | 人教版九年级数学下册教学讲义,复习补习资料(含知识讲解,巩固练习):56【基础】图形的相似与比例线段含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 92.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览


文档简介
图形的相似和比例线段--知识讲解(基础)
【学习目标】
1、能通过生活中的实例认识图形的相似,能通过观察直观地判断两个图形是否相似;
2、了解比例线段的概念及有关性质,探索相似图形的性质,知道两相似多边形的主要特征:对应角相等,对应边的比相等.明确相似比的含义;
3、知道两个相似的平面图形之间的关系,会根据相似多边形的特征识别两个多边形是否相似,并会运用性质进行相关的计算,提高推理能力.
【要点梳理】
要点一、比例线段
1.线段的比:
如果选用同一长度单位量得两条线段a、b长度分别是m、n,那么就说这两条线段的比是a:b=m:n ,或写成.
2.成比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.
3.比例的基本性质:
(1)若a:b=c:d ,则ad=bc;
(2)若a:b=b:c ,则 =ac(b称为a、c的比例中项).
要点二、相似图形
在数学上,我们把形状相同的图形称为相似图形(similar figures).
要点诠释: (1) 相似图形就是指形状相同,但大小不一定相同的图形; (2) “全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两个图形是全等;
要点三、相似多边形
相似多边形的概念:如果两个多边形的对应角相等,对应边的比相等,我们就说它们是相似多边形.
要点诠释:
(1)相似多边形的定义既是判定方法,又是它的性质.
(2)相似多边形对应边的比称为相似比.
【典型例题】
类型一、比例线段
1.(2019?甘肃模拟)若==(abc≠0),求的值.
【答案与解析】解:设===k,
则a=2k,b=3k,c=5k,
所以===.
【总结升华】本题考查了比例的性质.解题的关键是先假设===k,得出a=2k,b=3k,c=5k,降低计算难度.
举一反三:
【变式】(2019?兰州一模)若3a=2b,则的值为( )
A. B. C. D.
【答案】A
【解析】解:∵3a=2b,
∴=,
设a=2k,则b=3k,
则==﹣.
故选A.
类型二、相似图形
2.(2019?江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】解:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;
(2)等腰直角三角形都相似,正确;
(3)正方形都相似,正确;
(4)矩形对应边比值不一定相等,不矩形不一定都相似;
(5)正六边形都相似,正确,
故符合题意的有3个.故选:C.
【总结升华】此题主要考查了相似图形,应注意:
①相似图形的形状必须完全相同;
②相似图形的大小不一定相同;
③两个物体形状相同、大小相同时它们是全等的,全等是相似的一种特殊情况.
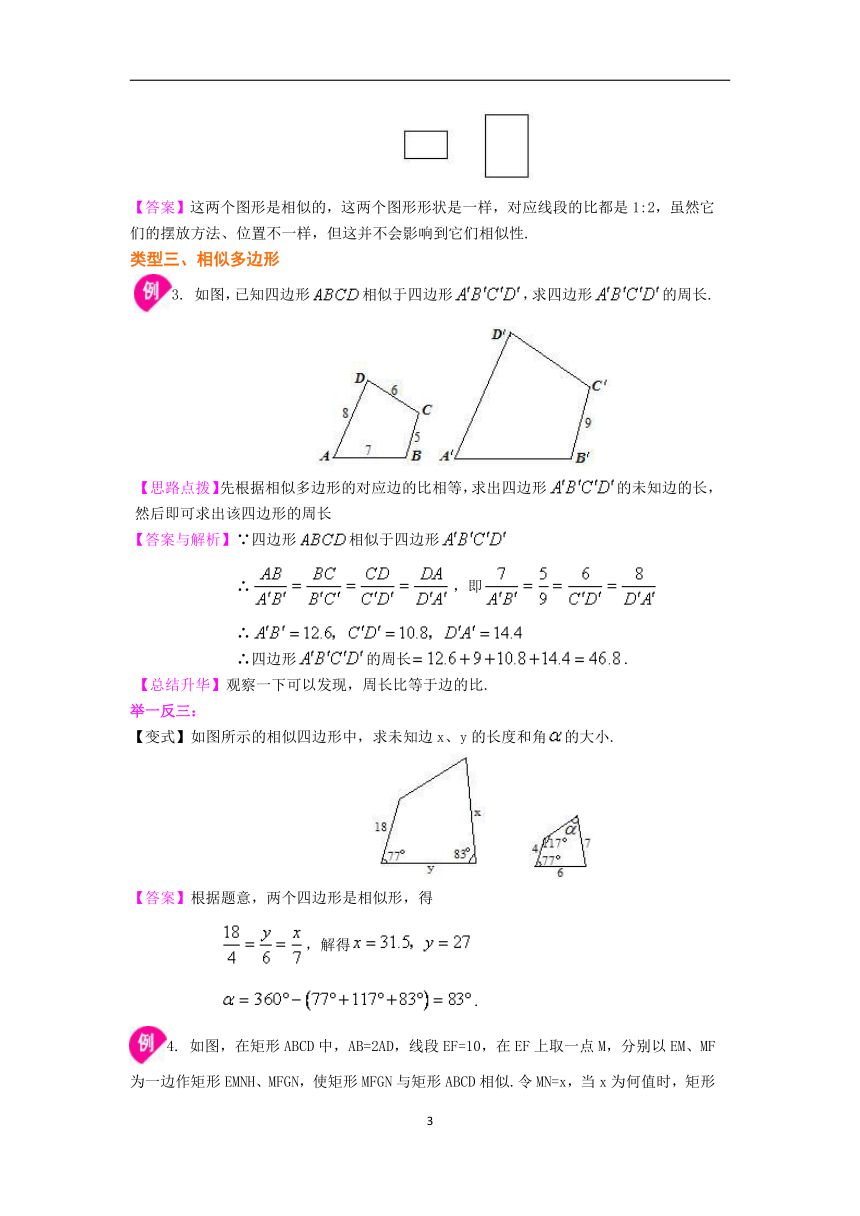
举一反三: 【变式】如图,左边是一个横放的长方形,右边的图形是把左边的长方形各边放大两倍,并竖立起来以后得到的,这两个图形是相似的吗? ?
【答案】这两个图形是相似的,这两个图形形状是一样,对应线段的比都是1:2,虽然它们的摆放方法、位置不一样,但这并不会影响到它们相似性.
类型三、相似多边形
3. 如图,已知四边形相似于四边形,求四边形的周长. 【思路点拨】先根据相似多边形的对应边的比相等,求出四边形的未知边的长,然后即可求出该四边形的周长
【答案与解析】∵四边形相似于四边形 ∴,即 ∴ ∴四边形的周长.
【总结升华】观察一下可以发现,周长比等于边的比.
举一反三: 【变式】如图所示的相似四边形中,求未知边x、y的长度和角的大小.
【答案】根据题意,两个四边形是相似形,得 ?,解得 ?.
4. 如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以EM、MF为一边作矩形EMNH、MFGN,使矩形MFGN与矩形ABCD相似.令MN=x,当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?
【答案与解析】 解:∵矩形MFGN与矩形ABCD相似 当时,S有最大值,最大值为.
【总结升华】借助相似,把最值问题转移到函数问题上,是解决这类题型最好方法之一.
图形的相似和比例线段--巩固练习(基础)
【巩固练习】
一.选择题
1.(2019秋?慈溪市期末)如图,用放大镜将图形放大,这种图形的改变是( )
A.相似 B.平移 C.轴对称 D.旋转
2. 下列四条线段中,不能成比例的是 ( ) A. =2,=4,=3,=6 B. =,=,=1,=
C. =6,=4,=10,=5 D. =,=2,=,=2
3. 下列命题正确的是( ) A.所有的等腰三角形都相似 B.所有的菱形都相似 C.所有的矩形都相似 D.所有的等腰直角三角形都相似
4. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是相似图形,如图所示,则小鱼上的点(a,b)对应大鱼上的点( ) A.(-2a,-2b) B.(-a,-2b) C.(-2b,-2a) D.(-2a,-b)
5. 一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则此三角形其它两边的和是( )A.19 B.17 C.24 D.21
6. .△ABC与△A1B1C1相似且相似比为,△A1B1C1与△A2B2C2相似且相似比为,则△ABC与△A2B2C2的相似比为 ( ) A. B. C.或 D.
二. 填空题
7. 两地实际距离为1 500 m,图上距离为5 cm,这张图的比例尺为_______.
8. 若,则________
9.判定两个多边形相似的方法是:当两个多边形的对应边_______,对应角_______时,两个多边形相似.
10.已知则
11.两个三角形相似,其中一个三角形两个内角分别是40°,60°,则另一个三角形的最大角为______,最小角为____________.
12.(2019春·庆阳校级月考) 要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一条最短边长为2,则另外一个三角形的周长为 .
三 综合题
13. (2019春?徐州校级月考)(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长;
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项,求线段c的长.
14. 如图,依次连接一个正方形各边的中点所形成的四边形与正方形相似吗?若相似,求出相似比;若不相似,说明理由.
15. 市场上供应的某种纸有如下特征:每次对折后,所得的长方形均和原长方形相似,则纸张(矩形)的长与宽应满足什么条件?
【答案与解析】
一、选择题 1.【答案】A
【解析】根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选A.
2.【答案】C.
【解析】求出最大与最小的两数的积,以及余下两数的积,看所得积是否相等来鉴别它们是否成比例.
3.【答案】 D
4.【答案】 A
【解析】 由图可知,小鱼和大鱼的相似比为1:2,若将小鱼放大1倍,则小鱼和大鱼关于原点对称.
5.【答案】C
【解析】相似三角形对应边的比相等
6.【答案】A
【解析】 相似比AB︰A1B1=,A1B1︰A2B2=,计算出AB︰A2B2.
二、填空题 7.【答案】.1:30 000
【解析】比例尺=图上距离︰实际距离.
8.【答案】?
【解析】由可得,故填.
9.【答案】成比例;相等.
10.【答案】
【解析】提示:设
11.【答案】80°,40°.
12.【答案】 7.5.
【解析】设另一个三角形周长是x.
∵一个三角形的三边长是4,5,6,
∴这个三角形的周长为:4+5+6=15.
∵与它相似的另一个三角形最短的一边长是2,
∴,
解得:x=7.5.
∴另一个三角形的周长是7.5.
三、解答题
13.【解析】解:(1)∵a、b、c、d是成比例线段,
∴a:b=c:d,
∵a=3cm,b=2cm,c=6cm,
∴d=4cm;
(2)∵线段c是线段a和b的比例中项,a=4cm,b=9cm.
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
14.【解析】要探究正方形是否与四边形相似,需知道四边形是否是正方形,若是正方形,则两正方形一定相似,若不是正方形,则不相似,因为所有的正方形都是相似的. 设正方形的边长为,由题意可知, 同理 由,可得 同理45°, ,四边形是正方形 ∴正方形?与正方形相似, 即两正方形的相似比是.
15.【解析】如图,为了方便分析可先画出草图,根据题意知两个矩形的长边之比应等于短边之比.
设矩形的长为,宽为,由相似多边形的特征得 ,即纸张的长与宽之比为.
【学习目标】
1、能通过生活中的实例认识图形的相似,能通过观察直观地判断两个图形是否相似;
2、了解比例线段的概念及有关性质,探索相似图形的性质,知道两相似多边形的主要特征:对应角相等,对应边的比相等.明确相似比的含义;
3、知道两个相似的平面图形之间的关系,会根据相似多边形的特征识别两个多边形是否相似,并会运用性质进行相关的计算,提高推理能力.
【要点梳理】
要点一、比例线段
1.线段的比:
如果选用同一长度单位量得两条线段a、b长度分别是m、n,那么就说这两条线段的比是a:b=m:n ,或写成.
2.成比例线段:对于四条线段a、b、c、d,如果其中两条线段的比与另两条线段的比相等,如a:b=c:d,我们就说这四条线段是成比例线段,简称比例线段.
3.比例的基本性质:
(1)若a:b=c:d ,则ad=bc;
(2)若a:b=b:c ,则 =ac(b称为a、c的比例中项).
要点二、相似图形
在数学上,我们把形状相同的图形称为相似图形(similar figures).
要点诠释: (1) 相似图形就是指形状相同,但大小不一定相同的图形; (2) “全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两个图形是全等;
要点三、相似多边形
相似多边形的概念:如果两个多边形的对应角相等,对应边的比相等,我们就说它们是相似多边形.
要点诠释:
(1)相似多边形的定义既是判定方法,又是它的性质.
(2)相似多边形对应边的比称为相似比.
【典型例题】
类型一、比例线段
1.(2019?甘肃模拟)若==(abc≠0),求的值.
【答案与解析】解:设===k,
则a=2k,b=3k,c=5k,
所以===.
【总结升华】本题考查了比例的性质.解题的关键是先假设===k,得出a=2k,b=3k,c=5k,降低计算难度.
举一反三:
【变式】(2019?兰州一模)若3a=2b,则的值为( )
A. B. C. D.
【答案】A
【解析】解:∵3a=2b,
∴=,
设a=2k,则b=3k,
则==﹣.
故选A.
类型二、相似图形
2.(2019?江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】解:(1)所有菱形的对应角不一定相等,故菱形不一定都相似;
(2)等腰直角三角形都相似,正确;
(3)正方形都相似,正确;
(4)矩形对应边比值不一定相等,不矩形不一定都相似;
(5)正六边形都相似,正确,
故符合题意的有3个.故选:C.
【总结升华】此题主要考查了相似图形,应注意:
①相似图形的形状必须完全相同;
②相似图形的大小不一定相同;
③两个物体形状相同、大小相同时它们是全等的,全等是相似的一种特殊情况.
举一反三: 【变式】如图,左边是一个横放的长方形,右边的图形是把左边的长方形各边放大两倍,并竖立起来以后得到的,这两个图形是相似的吗? ?
【答案】这两个图形是相似的,这两个图形形状是一样,对应线段的比都是1:2,虽然它们的摆放方法、位置不一样,但这并不会影响到它们相似性.
类型三、相似多边形
3. 如图,已知四边形相似于四边形,求四边形的周长. 【思路点拨】先根据相似多边形的对应边的比相等,求出四边形的未知边的长,然后即可求出该四边形的周长
【答案与解析】∵四边形相似于四边形 ∴,即 ∴ ∴四边形的周长.
【总结升华】观察一下可以发现,周长比等于边的比.
举一反三: 【变式】如图所示的相似四边形中,求未知边x、y的长度和角的大小.
【答案】根据题意,两个四边形是相似形,得 ?,解得 ?.
4. 如图,在矩形ABCD中,AB=2AD,线段EF=10,在EF上取一点M,分别以EM、MF为一边作矩形EMNH、MFGN,使矩形MFGN与矩形ABCD相似.令MN=x,当x为何值时,矩形EMNH的面积S有最大值?最大值是多少?
【答案与解析】 解:∵矩形MFGN与矩形ABCD相似 当时,S有最大值,最大值为.
【总结升华】借助相似,把最值问题转移到函数问题上,是解决这类题型最好方法之一.
图形的相似和比例线段--巩固练习(基础)
【巩固练习】
一.选择题
1.(2019秋?慈溪市期末)如图,用放大镜将图形放大,这种图形的改变是( )
A.相似 B.平移 C.轴对称 D.旋转
2. 下列四条线段中,不能成比例的是 ( ) A. =2,=4,=3,=6 B. =,=,=1,=
C. =6,=4,=10,=5 D. =,=2,=,=2
3. 下列命题正确的是( ) A.所有的等腰三角形都相似 B.所有的菱形都相似 C.所有的矩形都相似 D.所有的等腰直角三角形都相似
4. 某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是相似图形,如图所示,则小鱼上的点(a,b)对应大鱼上的点( ) A.(-2a,-2b) B.(-a,-2b) C.(-2b,-2a) D.(-2a,-b)
5. 一个三角形三边的长分别为3,5,7,另一个与它相似的三角形的最长边是21,则此三角形其它两边的和是( )A.19 B.17 C.24 D.21
6. .△ABC与△A1B1C1相似且相似比为,△A1B1C1与△A2B2C2相似且相似比为,则△ABC与△A2B2C2的相似比为 ( ) A. B. C.或 D.
二. 填空题
7. 两地实际距离为1 500 m,图上距离为5 cm,这张图的比例尺为_______.
8. 若,则________
9.判定两个多边形相似的方法是:当两个多边形的对应边_______,对应角_______时,两个多边形相似.
10.已知则
11.两个三角形相似,其中一个三角形两个内角分别是40°,60°,则另一个三角形的最大角为______,最小角为____________.
12.(2019春·庆阳校级月考) 要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为4、5、6,另一个三角形框架的一条最短边长为2,则另外一个三角形的周长为 .
三 综合题
13. (2019春?徐州校级月考)(1)已知a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,求线段d的长;
(2)已知线段a、b、c,a=4cm,b=9cm,线段c是线段a和b的比例中项,求线段c的长.
14. 如图,依次连接一个正方形各边的中点所形成的四边形与正方形相似吗?若相似,求出相似比;若不相似,说明理由.
15. 市场上供应的某种纸有如下特征:每次对折后,所得的长方形均和原长方形相似,则纸张(矩形)的长与宽应满足什么条件?
【答案与解析】
一、选择题 1.【答案】A
【解析】根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选A.
2.【答案】C.
【解析】求出最大与最小的两数的积,以及余下两数的积,看所得积是否相等来鉴别它们是否成比例.
3.【答案】 D
4.【答案】 A
【解析】 由图可知,小鱼和大鱼的相似比为1:2,若将小鱼放大1倍,则小鱼和大鱼关于原点对称.
5.【答案】C
【解析】相似三角形对应边的比相等
6.【答案】A
【解析】 相似比AB︰A1B1=,A1B1︰A2B2=,计算出AB︰A2B2.
二、填空题 7.【答案】.1:30 000
【解析】比例尺=图上距离︰实际距离.
8.【答案】?
【解析】由可得,故填.
9.【答案】成比例;相等.
10.【答案】
【解析】提示:设
11.【答案】80°,40°.
12.【答案】 7.5.
【解析】设另一个三角形周长是x.
∵一个三角形的三边长是4,5,6,
∴这个三角形的周长为:4+5+6=15.
∵与它相似的另一个三角形最短的一边长是2,
∴,
解得:x=7.5.
∴另一个三角形的周长是7.5.
三、解答题
13.【解析】解:(1)∵a、b、c、d是成比例线段,
∴a:b=c:d,
∵a=3cm,b=2cm,c=6cm,
∴d=4cm;
(2)∵线段c是线段a和b的比例中项,a=4cm,b=9cm.
∴c2=ab=36,
解得:c=±6,
又∵线段是正数,
∴c=6cm.
14.【解析】要探究正方形是否与四边形相似,需知道四边形是否是正方形,若是正方形,则两正方形一定相似,若不是正方形,则不相似,因为所有的正方形都是相似的. 设正方形的边长为,由题意可知, 同理 由,可得 同理45°, ,四边形是正方形 ∴正方形?与正方形相似, 即两正方形的相似比是.
15.【解析】如图,为了方便分析可先画出草图,根据题意知两个矩形的长边之比应等于短边之比.
设矩形的长为,宽为,由相似多边形的特征得 ,即纸张的长与宽之比为.
