人教版九年级上册数学21.2.4 一元二次方程根与系数的关系 复习课课件 (共23张PPT)
文档属性
| 名称 | 人教版九年级上册数学21.2.4 一元二次方程根与系数的关系 复习课课件 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1006.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-21 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
21.2.4 一元二次方程根与系数的关系
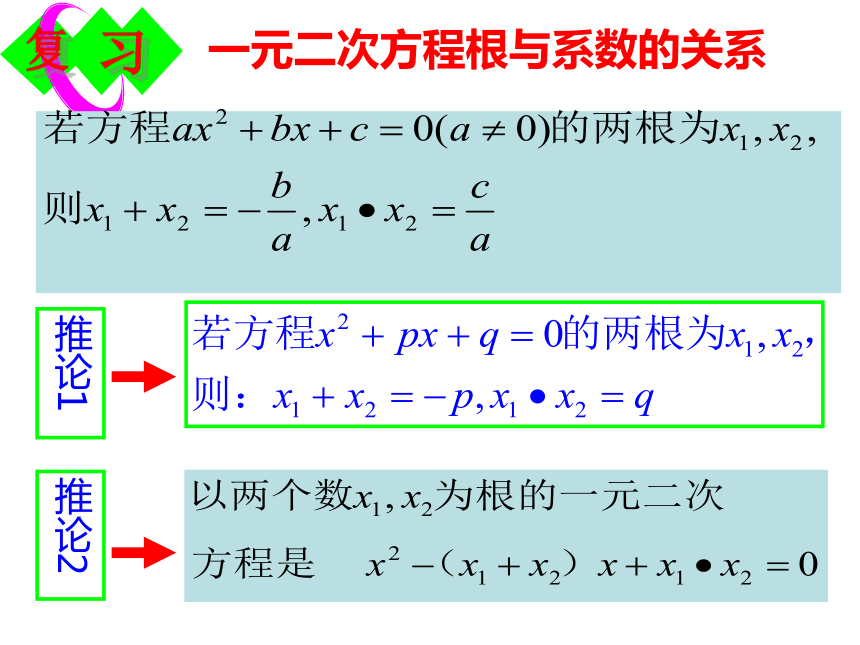
一元二次方程根与系数的关系
推论1
推论2
说出下列各方程的两根之和与两根之积:
(1) x2 - 2x - 1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
在使用韦达定理时,应注意:
⑴、不是一般式的要先化成一般式;
⑵、在使用X1+X2=- 时,注意“- ”不要漏写。
(3) 前提是方程有实数根即Δ≥0
几种常见的求代数式的值
引申:1、若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,
(2)若两根互为倒数,
(3)若一根为0,
(4)若一根为1,
(5)若一根为?1,
(6)若a、c异号,
补充规律:
则b?0;
则a?c;
则c?0 ;
则a?b?c?0 ;
则a?b?c?0;
方程一定有两个实数根.
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法一:
设方程的另一个根为x1.
由韦达定理,得
x1 +2= k+1
x1 ●2= 3k
解这方程组,得
x1 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2。
作用1:已知方程一根,求另一根及未知数。
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法二:
设方程的另一个根为x1.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由韦达定理,得x1●2=3k
即2 x1 =-6
∴ x1 =-3
答:方程的另一个根是-3 , k的值是-2。
作用1:已知方程一根,求另一根及未知数。
解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即
所以:
得:
例2.方程 的两根互为倒数,求k的值。
例3.方程3x2+x+k=0的两根之积为-3,求k的值。
解:设方程的两根分别为x1和x2,
则:x1·x2=
∴ k=-9
例1.已知两个数的和是1,积是-2,求这两 个数。
解法一:设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法二:设两数分别为一个一元二次方程
的两根则:
求得
∴这两个数为2和-1
作用2:已知两个数的和与积,求两数
例2.已知两数之和为14,乘积为-51,求这两数.
设这两数为 m, n,
解:
m, n可以看作是方程 x2-14x-51=0的两个根
∴这两数为17,-3
作用2:已知两个数的和与积,求两数
作用3:求代数式的值
例1、已知2x2-x-2=0的两根是x1 , x2 。求下列代数式的值。
(1) x12+x22 (2) (3) (x1-x2)2
解:⑴∵x1+x2= , x1 · x2=-1
∴x12+x22 =(x1+x2)2 -2x1x2
(2)∵x1+x2= , x1 · x2=-1
(3)∵x1+x2= , x1 · x2=-1
∴(x1-x2)2=x12+x22-2x1x2
=(x1+x2)2-4x1x2
例2.已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
x1+x2=-k, x1·x2=k+2
又 x12+ x2 2 = 4
即(x1+ x2)2 -2x1x2=4
K2 -2(k+2)=4
K2 -2k-8=0
解得:k=4 或k=-2
∵ △= K2-4k-8
当k=4时, △=-8<0
∴k=4(舍去)
当k=-2时,△=4>0
∴ k=-2
1.已知a、b是一元二次方程x2+3x-7=0的两个实数根,求代数式a2+4a+b的值
解:∵a、b是一元二次方程x2+3x-7=0的两个实数根
∴a2+3a-7=0,a+b=-3,
则a2+4a+b=a2+3a+a+b=7-3=4.
课堂练习
作业:已知m、n是方程x2-3x+1=0的两根,求2m2+4n2-6n+2014的值。
2.已知x1、x2是方程x2+(m-2)x+2=0的两个实数根,求(2+mx1+x12)(2+mx2+x22)的值。
解:∵x12+(m-2)x1+2=0 , x22+(m-2)x2+2=0
∴x12+2=2x1-mx1 , x22+2=2x2-mx2
又∵x1x2=2
原式=(2x1-mx1+mx1)(2x2-mx2+mx2)
=2x1·2x2
=4x1x2
=4×2
=8
3.已知:x1、x2是方程x2-x+a=0的两个实数根,
且 ,求a的值.
解:据题意得x1+x2=1;x1·x2=a
∴a=1/3舍去,∴a= -1.
*4. (孝感中考)已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x-x=0时,求m的值.
5.已知关于 x 的方程 x2+2(m-2)x+m2+4=0
有两个实数根,并且这两个根的平方和比
两根的积大21。求m的值。
解∵△=4(m-2)2-4(m2+4) =-16m≥0
∴m≤0
设方程两个根为x1、x2,则由题意:
x1+x2 = -2(m-2) , x1x2 = m?+4
x12+x22 - x1x2=21
(x1+x2)2 - 3x1x2 = 21
4(m-2)2 - 3(m2+4) = 21
m2 - 16m - 17 = 0
∴m1 = -1 ,m2=17(不符合m≤0,舍去)
∴m = -1
6.当m为何值时,2x2-3mx+2m+3=0的一个根是另一个根的两倍.
解:设两根分别为
则由韦达定理得:
①
②
∴①2÷ ②得
7.已知一元二次方程2x2-mx-2m+1=0的两根的平方和是 ,求的m值 。
解:设方程两根为x1,x2. 则
解得:m1=-11, m2=3
当m=-11时,方程为2x2+11x+23=0, ⊿=112-4×2×23<0,方程无实数根,∴m=-11不合题意,舍去
当m=3时,方程为2x2-3x-5=0, ⊿=(-3)2-4×2×(-5) >0,方程有两个不相等的实数根.
∴m的值为3
解:① ⊿=42-4k·(-3) >0 且k≠0
∴k> 且k≠0
∴存在满足条件的k值,且k=4
例1:已知方程 x2-2(k-1)x+k2-2=0
解:
(1)设方程的两个根为x1,x2,
则x1 < 0 ,x2 < 0
作用5:研究方程根的情况
(1)k 为何值时,方程有两个负数根?
例1:已知方程 x2-2(k-1)x+k2-2=0
(2)k 为何值时,方程有一正根和负根?
解:
(2)设方程的两个根为x1,x2,
则x1 < 0 ,x2 > 0
作用5:研究方程根的情况
补充规律:
一正根,一负根
{
△>0
x1x2<0
两个正根
{
△≥0
x1x2>0
x1+x2>0
两个负根
{
△≥0
x1x2>0
x1+x2<0
<
>0
>0
例2:方程
有一个正根,一个负根,求m的取值范围。
∴
△=
{
即
{
m>0
m-1<0
∴0解:设方程的两个根为x1,x2,
则x1 < 0 ,x2 > 0
21.2.4 一元二次方程根与系数的关系
一元二次方程根与系数的关系
推论1
推论2
说出下列各方程的两根之和与两根之积:
(1) x2 - 2x - 1=0
(3) 2x2 - 6x =0
(4) 3x2 = 4
x1+x2=2
x1x2=-1
x1+x2=
x1+x2=3
x1+x2=0
x1x2=
x1x2=0
x1x2= -
在使用韦达定理时,应注意:
⑴、不是一般式的要先化成一般式;
⑵、在使用X1+X2=- 时,注意“- ”不要漏写。
(3) 前提是方程有实数根即Δ≥0
几种常见的求代数式的值
引申:1、若ax2?bx?c?0 (a?0 ??0)
(1)若两根互为相反数,
(2)若两根互为倒数,
(3)若一根为0,
(4)若一根为1,
(5)若一根为?1,
(6)若a、c异号,
补充规律:
则b?0;
则a?c;
则c?0 ;
则a?b?c?0 ;
则a?b?c?0;
方程一定有两个实数根.
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法一:
设方程的另一个根为x1.
由韦达定理,得
x1 +2= k+1
x1 ●2= 3k
解这方程组,得
x1 =-3
k =-2
答:方程的另一个根是-3 , k的值是-2。
作用1:已知方程一根,求另一根及未知数。
例1、已知方程x2-(k+1)x+3k=0的一个根是2 ,
求它的另一个根及k的值。
解法二:
设方程的另一个根为x1.
把x=2代入方程,得 4-2(k+1)+3k=0
解这方程,得 k= - 2
由韦达定理,得x1●2=3k
即2 x1 =-6
∴ x1 =-3
答:方程的另一个根是-3 , k的值是-2。
作用1:已知方程一根,求另一根及未知数。
解:设方程的两根分别为 和 ,
则:
而方程的两根互为倒数
即
所以:
得:
例2.方程 的两根互为倒数,求k的值。
例3.方程3x2+x+k=0的两根之积为-3,求k的值。
解:设方程的两根分别为x1和x2,
则:x1·x2=
∴ k=-9
例1.已知两个数的和是1,积是-2,求这两 个数。
解法一:设两数分别为x,y则:
{
解得:
x=2
y=-1
{
或
x=-1
y=2
{
解法二:设两数分别为一个一元二次方程
的两根则:
求得
∴这两个数为2和-1
作用2:已知两个数的和与积,求两数
例2.已知两数之和为14,乘积为-51,求这两数.
设这两数为 m, n,
解:
m, n可以看作是方程 x2-14x-51=0的两个根
∴这两数为17,-3
作用2:已知两个数的和与积,求两数
作用3:求代数式的值
例1、已知2x2-x-2=0的两根是x1 , x2 。求下列代数式的值。
(1) x12+x22 (2) (3) (x1-x2)2
解:⑴∵x1+x2= , x1 · x2=-1
∴x12+x22 =(x1+x2)2 -2x1x2
(2)∵x1+x2= , x1 · x2=-1
(3)∵x1+x2= , x1 · x2=-1
∴(x1-x2)2=x12+x22-2x1x2
=(x1+x2)2-4x1x2
例2.已知方程 的两个实数根
是 且 求k的值。
解:由根与系数的关系得
x1+x2=-k, x1·x2=k+2
又 x12+ x2 2 = 4
即(x1+ x2)2 -2x1x2=4
K2 -2(k+2)=4
K2 -2k-8=0
解得:k=4 或k=-2
∵ △= K2-4k-8
当k=4时, △=-8<0
∴k=4(舍去)
当k=-2时,△=4>0
∴ k=-2
1.已知a、b是一元二次方程x2+3x-7=0的两个实数根,求代数式a2+4a+b的值
解:∵a、b是一元二次方程x2+3x-7=0的两个实数根
∴a2+3a-7=0,a+b=-3,
则a2+4a+b=a2+3a+a+b=7-3=4.
课堂练习
作业:已知m、n是方程x2-3x+1=0的两根,求2m2+4n2-6n+2014的值。
2.已知x1、x2是方程x2+(m-2)x+2=0的两个实数根,求(2+mx1+x12)(2+mx2+x22)的值。
解:∵x12+(m-2)x1+2=0 , x22+(m-2)x2+2=0
∴x12+2=2x1-mx1 , x22+2=2x2-mx2
又∵x1x2=2
原式=(2x1-mx1+mx1)(2x2-mx2+mx2)
=2x1·2x2
=4x1x2
=4×2
=8
3.已知:x1、x2是方程x2-x+a=0的两个实数根,
且 ,求a的值.
解:据题意得x1+x2=1;x1·x2=a
∴a=1/3舍去,∴a= -1.
*4. (孝感中考)已知关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.
(1)求实数m的取值范围;
(2)当x-x=0时,求m的值.
5.已知关于 x 的方程 x2+2(m-2)x+m2+4=0
有两个实数根,并且这两个根的平方和比
两根的积大21。求m的值。
解∵△=4(m-2)2-4(m2+4) =-16m≥0
∴m≤0
设方程两个根为x1、x2,则由题意:
x1+x2 = -2(m-2) , x1x2 = m?+4
x12+x22 - x1x2=21
(x1+x2)2 - 3x1x2 = 21
4(m-2)2 - 3(m2+4) = 21
m2 - 16m - 17 = 0
∴m1 = -1 ,m2=17(不符合m≤0,舍去)
∴m = -1
6.当m为何值时,2x2-3mx+2m+3=0的一个根是另一个根的两倍.
解:设两根分别为
则由韦达定理得:
①
②
∴①2÷ ②得
7.已知一元二次方程2x2-mx-2m+1=0的两根的平方和是 ,求的m值 。
解:设方程两根为x1,x2. 则
解得:m1=-11, m2=3
当m=-11时,方程为2x2+11x+23=0, ⊿=112-4×2×23<0,方程无实数根,∴m=-11不合题意,舍去
当m=3时,方程为2x2-3x-5=0, ⊿=(-3)2-4×2×(-5) >0,方程有两个不相等的实数根.
∴m的值为3
解:① ⊿=42-4k·(-3) >0 且k≠0
∴k> 且k≠0
∴存在满足条件的k值,且k=4
例1:已知方程 x2-2(k-1)x+k2-2=0
解:
(1)设方程的两个根为x1,x2,
则x1 < 0 ,x2 < 0
作用5:研究方程根的情况
(1)k 为何值时,方程有两个负数根?
例1:已知方程 x2-2(k-1)x+k2-2=0
(2)k 为何值时,方程有一正根和负根?
解:
(2)设方程的两个根为x1,x2,
则x1 < 0 ,x2 > 0
作用5:研究方程根的情况
补充规律:
一正根,一负根
{
△>0
x1x2<0
两个正根
{
△≥0
x1x2>0
x1+x2>0
两个负根
{
△≥0
x1x2>0
x1+x2<0
<
>0
>0
例2:方程
有一个正根,一个负根,求m的取值范围。
∴
△=
{
即
{
m>0
m-1<0
∴0
则x1 < 0 ,x2 > 0
同课章节目录
