北师大版 六年级下册总复习 数与代数 4正比例与反比例 第13课时课件(23张PPT)
文档属性
| 名称 | 北师大版 六年级下册总复习 数与代数 4正比例与反比例 第13课时课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 412.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 21:17:36 | ||
图片预览








文档简介
课件23张PPT。第13课时 正比例与反比例 北师大版 数学 六年级 下册总复习 数与代数 1.使学生进一步理解比的意义和基本性质以及比、分数与除法的关系;理解比的基本性质与分数的基本性质、商不变的规律内在一致性;理解比例的意义和基本性质。
2.能运用比和比例的知识解决一些简单实际问题,丰富解决问题策略,积累解决问题的经验。
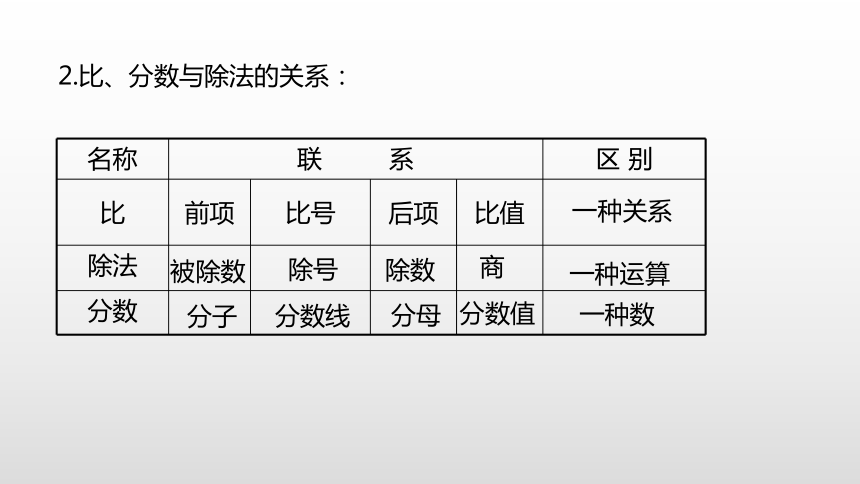
3.通过一题多变、一题多解等形式,由浅入深,由易到难,培养学生思维的灵活性。 【重点】能运用比和比例的知识解决一些简单实际问题。【难点】解决一题多变、一题多解等形式的实际问题。 1.比和比例的意义与性质 两个数相除又叫作两个数的比。表示两个比相等的式子叫作比例。比的前项和后项同时乘或除以相同的数(0除外),比值不变。在比例里,两个外项的积等于两个内项的积。前项 比号 后项 比值 6 : 4 = 1.5 6 : 4 = 3 : 2 外项 内项 内项 外项 各部分名称2.比、分数与除法的关系:a∶b= =( )÷( )(b≠0)ab338240.375想:3:8的前项加上15,要使比值不变,后项应加上( )。40ab被除数分子除号分数线除数分母一种数一种运算一种关系商分数值2.比、分数与除法的关系:3.求比值和化简比:求比值结果是一个数 (2)化简比:
根据比的基本性质,把比的前项和后项都乘或除以相同的数(零除外),结果是一个比,它的前项和后项是互质数。(两个互质数都是正整数)
12:14=6:7
500千克:1吨=500千克:1000千克=1:2化简比结果是一个比=3∶2=2∶120∶2045∶30=15∶10(1)量出每幅照片的长和宽,并分别写出它们的比。(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。45∶3030∶1515∶10=1∶1=3∶2图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离 = 比例尺4.比例尺分类
数值比例尺 如:1:10000000
线段比例尺 如:注意:
(1)比例尺与一般的尺不同,它是一个比,且仅是长度比,不应带有计量单位。
(2)求比例尺时,前、后项的单位长度一定要化成同级单位。
(3)为了计算简便,比例尺的前项或后项,一般应化简成“1”。
(4)比例尺中的前项和后项不能颠倒。
(5)题中没有给出说明时,图上距离一般用厘米作单位。5.正比例和反比例的区别与联系: 两种相关联的量,一种量变化,另一种也随着变化。一种量扩大(缩小),另一种量也随着扩大(缩小)两种量的比值一定一种量扩大(缩小),另一种量反而缩小(扩大)两种量的积一定在一个等腰三角形中,其中一个角的度数为40°,你知道顶角和底角的比是( )或( )。4 ∶ 75 ∶ 2下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?1.正方形的周长与边长。( )成正比例2.小丽步行上学的平均速度与所花时间。( ) 成反比例不成比例4.全班人数一定,出勤人数和缺勤人数。( )不成比例5.全班人数一定,出勤人数和出勤率。 ( )成正比例3.每年体检你们班级视力正常的人数与近视的人数。( ) 深色:淡色=20:40=1:2深色:15÷3×1=5(平方米)一个房间的地面由两种颜色的地砖铺成。(1)写出两种地砖铺地面积的比,并化简。(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?淡色:15÷3×2=10(平方米)在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米/时?两地实距:5×60=300(千米)速度和:300÷3=100(千米)甲速度:100÷5×2
=20×2
=40(千米/时)在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米/时?乙速度:100÷5×3
=20×3
=60(千米/时)检验:40:60=2:3 (40+60)×3=300(千米)
5厘米:300千米=5:30000000=1:6000000答:甲速度是40千米/时,乙速度是60千米/时。(1) 两个正方形的边长比是 1∶ 3 , 周长比是( ) , 面积比是( ) 。
(2) 9 元可以买 2 kg 鸡蛋, 总价与数量的比是( ) , 比值是( ) 。
(3) 汽车 3 时行 150 km, 路程与时间的比是( ) , 比值是( ) 。1:31:99:24.5150:3501填空。1(4)订阅《学习报》的份数和钱数成( )比例。 (5)如果每千克梨6元,那么梨的数量与总价成( )比例。 (6)如果一个长方形的面积是30平方分米,那么长与宽成( )比例。
(7)一种微型零件的长5毫米,画在图纸上长20厘米,这幅图的比例尺是( )。正正反40:1填空。1、圆的面积和圆的半径的平方成正比例。( )
2、正方形的面积和边长成正比例。( )
3、长方形的周长一定时,长和宽成反比例。 ( )
4、三角形的面积一定时,底和高成反比例。( )
5、梯形的面积一定时,上底和下底的和与高成反比例。 ( )
6、圆的周长和圆的半径成正比例。( )√ⅹ×√√√ 判断。2?=1:4=6:1=5:12=30:13化简。=1:15 =5:32=1:2=4:3 解方程。 ?解: 0.5χ=4
0.5χ÷0.5=4÷0.5
χ=8?解:2χ=2.5ⅹ2.8
2χ=7
2χ÷2=7÷2
χ=3.5 45(1)求这幅图的比例尺。图上距离∶实际距离 = 比例尺在一幅地图上,测得甲、乙两地的图上距离是12厘米,已知甲乙两地的实际距离是480千米。答:这幅图的比例尺是1:4000000。 480千米=48000000厘米
12cm∶480km= 12∶48000000=1∶400000051:4000000表示图上1厘米实际40千米
4×40=160(千米)答:A、B两地的实际距离是160千米。(2)在这幅地图上量得A、B两城的图上距离是4厘米,求A、B两城的实际距离。在一幅地图上,测得甲、乙两地的图上距离是12厘米,已知甲乙两地的实际距离是480千米。
2.能运用比和比例的知识解决一些简单实际问题,丰富解决问题策略,积累解决问题的经验。
3.通过一题多变、一题多解等形式,由浅入深,由易到难,培养学生思维的灵活性。 【重点】能运用比和比例的知识解决一些简单实际问题。【难点】解决一题多变、一题多解等形式的实际问题。 1.比和比例的意义与性质 两个数相除又叫作两个数的比。表示两个比相等的式子叫作比例。比的前项和后项同时乘或除以相同的数(0除外),比值不变。在比例里,两个外项的积等于两个内项的积。前项 比号 后项 比值 6 : 4 = 1.5 6 : 4 = 3 : 2 外项 内项 内项 外项 各部分名称2.比、分数与除法的关系:a∶b= =( )÷( )(b≠0)ab338240.375想:3:8的前项加上15,要使比值不变,后项应加上( )。40ab被除数分子除号分数线除数分母一种数一种运算一种关系商分数值2.比、分数与除法的关系:3.求比值和化简比:求比值结果是一个数 (2)化简比:
根据比的基本性质,把比的前项和后项都乘或除以相同的数(零除外),结果是一个比,它的前项和后项是互质数。(两个互质数都是正整数)
12:14=6:7
500千克:1吨=500千克:1000千克=1:2化简比结果是一个比=3∶2=2∶120∶2045∶30=15∶10(1)量出每幅照片的长和宽,并分别写出它们的比。(2)先估计哪两个比能组成比例,再算一算,看估计得对不对。45∶3030∶1515∶10=1∶1=3∶2图上距离和实际距离的比,叫作这幅图的比例尺。
图上距离∶实际距离 = 比例尺4.比例尺分类
数值比例尺 如:1:10000000
线段比例尺 如:注意:
(1)比例尺与一般的尺不同,它是一个比,且仅是长度比,不应带有计量单位。
(2)求比例尺时,前、后项的单位长度一定要化成同级单位。
(3)为了计算简便,比例尺的前项或后项,一般应化简成“1”。
(4)比例尺中的前项和后项不能颠倒。
(5)题中没有给出说明时,图上距离一般用厘米作单位。5.正比例和反比例的区别与联系: 两种相关联的量,一种量变化,另一种也随着变化。一种量扩大(缩小),另一种量也随着扩大(缩小)两种量的比值一定一种量扩大(缩小),另一种量反而缩小(扩大)两种量的积一定在一个等腰三角形中,其中一个角的度数为40°,你知道顶角和底角的比是( )或( )。4 ∶ 75 ∶ 2下面各题中的两个量,哪些成正比例,哪些成反比例,哪些既不成正比例也不成反比例?1.正方形的周长与边长。( )成正比例2.小丽步行上学的平均速度与所花时间。( ) 成反比例不成比例4.全班人数一定,出勤人数和缺勤人数。( )不成比例5.全班人数一定,出勤人数和出勤率。 ( )成正比例3.每年体检你们班级视力正常的人数与近视的人数。( ) 深色:淡色=20:40=1:2深色:15÷3×1=5(平方米)一个房间的地面由两种颜色的地砖铺成。(1)写出两种地砖铺地面积的比,并化简。(2)如果这个房间的面积是15平方米,两种地砖的铺地面积分别是多少平方米?淡色:15÷3×2=10(平方米)在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米/时?两地实距:5×60=300(千米)速度和:300÷3=100(千米)甲速度:100÷5×2
=20×2
=40(千米/时)在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米/时?乙速度:100÷5×3
=20×3
=60(千米/时)检验:40:60=2:3 (40+60)×3=300(千米)
5厘米:300千米=5:30000000=1:6000000答:甲速度是40千米/时,乙速度是60千米/时。(1) 两个正方形的边长比是 1∶ 3 , 周长比是( ) , 面积比是( ) 。
(2) 9 元可以买 2 kg 鸡蛋, 总价与数量的比是( ) , 比值是( ) 。
(3) 汽车 3 时行 150 km, 路程与时间的比是( ) , 比值是( ) 。1:31:99:24.5150:3501填空。1(4)订阅《学习报》的份数和钱数成( )比例。 (5)如果每千克梨6元,那么梨的数量与总价成( )比例。 (6)如果一个长方形的面积是30平方分米,那么长与宽成( )比例。
(7)一种微型零件的长5毫米,画在图纸上长20厘米,这幅图的比例尺是( )。正正反40:1填空。1、圆的面积和圆的半径的平方成正比例。( )
2、正方形的面积和边长成正比例。( )
3、长方形的周长一定时,长和宽成反比例。 ( )
4、三角形的面积一定时,底和高成反比例。( )
5、梯形的面积一定时,上底和下底的和与高成反比例。 ( )
6、圆的周长和圆的半径成正比例。( )√ⅹ×√√√ 判断。2?=1:4=6:1=5:12=30:13化简。=1:15 =5:32=1:2=4:3 解方程。 ?解: 0.5χ=4
0.5χ÷0.5=4÷0.5
χ=8?解:2χ=2.5ⅹ2.8
2χ=7
2χ÷2=7÷2
χ=3.5 45(1)求这幅图的比例尺。图上距离∶实际距离 = 比例尺在一幅地图上,测得甲、乙两地的图上距离是12厘米,已知甲乙两地的实际距离是480千米。答:这幅图的比例尺是1:4000000。 480千米=48000000厘米
12cm∶480km= 12∶48000000=1∶400000051:4000000表示图上1厘米实际40千米
4×40=160(千米)答:A、B两地的实际距离是160千米。(2)在这幅地图上量得A、B两城的图上距离是4厘米,求A、B两城的实际距离。在一幅地图上,测得甲、乙两地的图上距离是12厘米,已知甲乙两地的实际距离是480千米。
