第三单元长方体与正方体第12课时课件(20张PPT)
文档属性
| 名称 | 第三单元长方体与正方体第12课时课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 181.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 12:20:49 | ||
图片预览




文档简介
课件20张PPT。长方体与正方体第12课时 整理与复习人教版 数学 五年级 下册探索规律并进行归纳总结。1.进一步认识和理解正方体的特征。
2.通过观察、列表、想象等活动,经历发现正方体涂色和位置的规律
的全过程,获得化繁为简的解决问题的经验,培养空间想象力。
3.体会分类、数形结合、归纳、推理等数学思想,积累数学思维活动的经验。学会从简单的情况入手寻找规律,把复杂问题化繁为简的思想
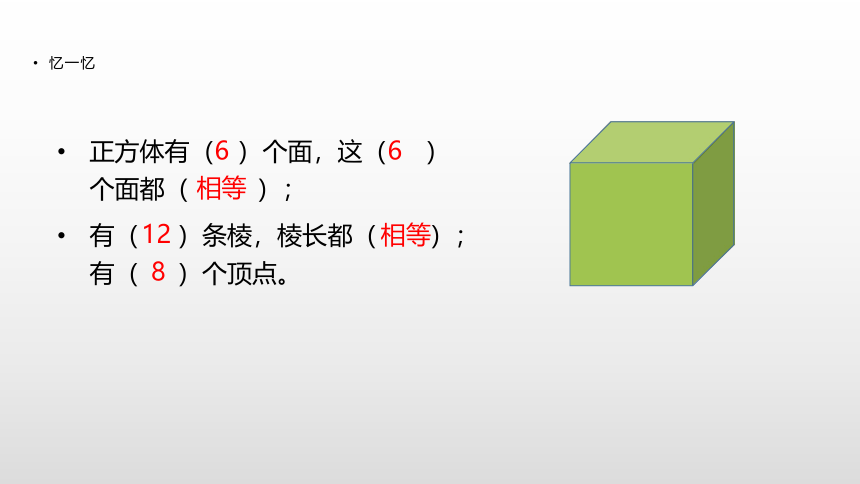
方法。忆一忆正方体有( )个面,这( )个面都( );
有( )条棱,棱长都( );有( )个顶点。
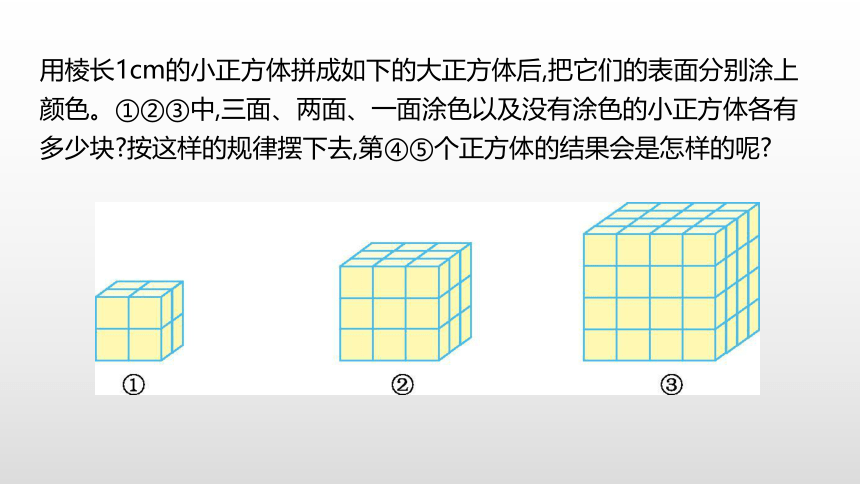
66相等12相等8用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①②③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第④⑤个正方体的结果会是怎样的呢?1.用棱长1 cm的小正方体拼成棱长为2 cm的大正方体。(1)用棱长1 cm的小正方体拼成棱长为2 cm的大正方体后,
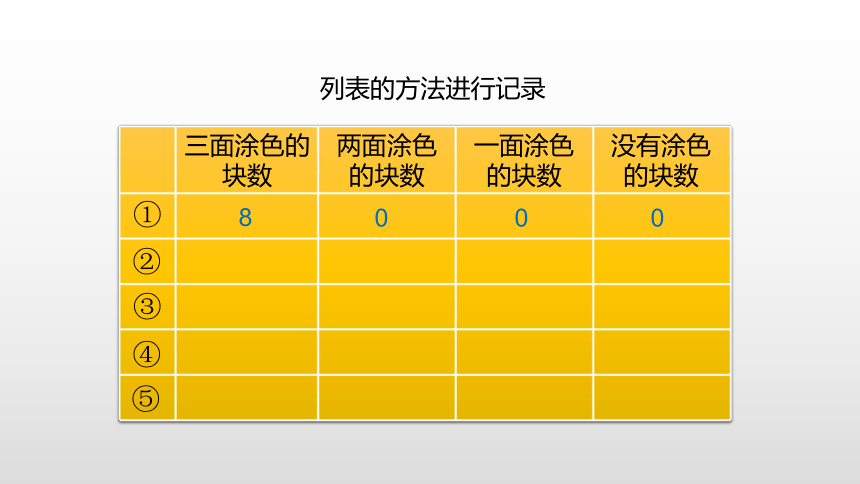
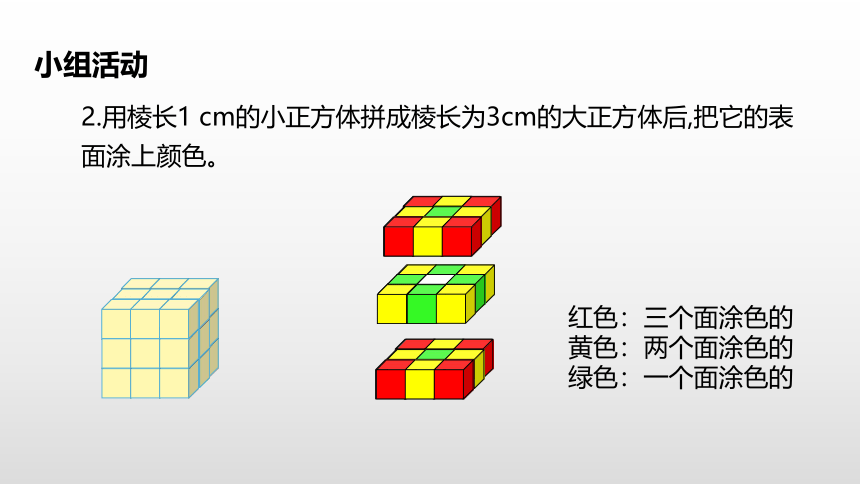
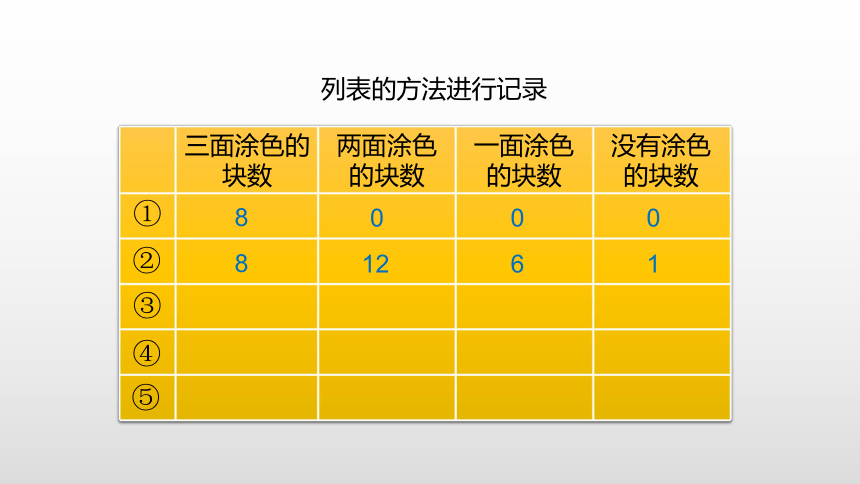
把它的表面涂上颜色。小组活动1.用棱长1 cm的小正方体拼成棱长为2 cm的大正方体。(2)议一议:需要多少个小正方体?你觉得这些小正方体涂色的面有什么特点? 小组活动在大正方体8个顶点的位置。需要8个小正方体, 8个小正方体都有三面涂上了颜色。三面都涂色的小正方体在大正方体的什么位置?列表的方法进行记录8000①②③④⑤2.用棱长1 cm的小正方体拼成棱长为3cm的大正方体后,把它的表面涂上颜色。小组活动红色:三个面涂色的
黄色:两个面涂色的
绿色:一个面涂色的列表的方法进行记录8000①②③④⑤812613.用棱长1 cm的小正方体拼成棱长为4cm的大正方体后,把它的表面涂上颜色。小组活动列表的方法进行记录8000①②③④⑤81261824248836542784896648000①②③④⑤81×12=121×1×6=61×1×1=182×12=242×2×6=242×2×2=883×12=363×3×6=543×3×3=2784×12=484×4×6=964×4×4=64观察上表,你能发现什么?在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。没有涂色的块数与面有关,即(n-2)2,或用总块数-三面涂色的块数-两面涂色的块数-一面涂色的块数。或343-8-60-150=125(个)棱长是7厘米的正方体中三面涂色的有几块?两面涂色的有几块?一面涂色的有几块?没有涂色的有几块?三面涂色8个两面涂色:(7-2)×12=60(个)一面涂色:(7-2)2×6=150(个)没有涂色的:(7-2)3=125(个)你还能继续写出第⑥、⑦、⑧个大正方体中4类正方体的块数吗?1把棱长为1厘米的小正方体拼成棱长为n的大正方体后涂色,涂色面的规律:
(1)三面涂色的小正方体个数=正方体的顶点个数=8。
(2)两面涂色的小正方体个数=12×(n-2)。
(3)一面涂色的小正方体个数=6×(n-2)2。
(4)没有涂色的小正方体个数=(n-2)3。这节课你有什么收获?如果摆成下面的几何体你会数吗?第1个图形中小正方体的个数:1+(1+2)=4;第2个图形中小正方体的个数:1+(1+2)+(1+2+3)=10;第3个图形中小正方体的个数:
1+(1+2)+(1+2+3)+(1+2+3+4)=20。1
2.通过观察、列表、想象等活动,经历发现正方体涂色和位置的规律
的全过程,获得化繁为简的解决问题的经验,培养空间想象力。
3.体会分类、数形结合、归纳、推理等数学思想,积累数学思维活动的经验。学会从简单的情况入手寻找规律,把复杂问题化繁为简的思想
方法。忆一忆正方体有( )个面,这( )个面都( );
有( )条棱,棱长都( );有( )个顶点。
66相等12相等8用棱长1cm的小正方体拼成如下的大正方体后,把它们的表面分别涂上颜色。①②③中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?按这样的规律摆下去,第④⑤个正方体的结果会是怎样的呢?1.用棱长1 cm的小正方体拼成棱长为2 cm的大正方体。(1)用棱长1 cm的小正方体拼成棱长为2 cm的大正方体后,
把它的表面涂上颜色。小组活动1.用棱长1 cm的小正方体拼成棱长为2 cm的大正方体。(2)议一议:需要多少个小正方体?你觉得这些小正方体涂色的面有什么特点? 小组活动在大正方体8个顶点的位置。需要8个小正方体, 8个小正方体都有三面涂上了颜色。三面都涂色的小正方体在大正方体的什么位置?列表的方法进行记录8000①②③④⑤2.用棱长1 cm的小正方体拼成棱长为3cm的大正方体后,把它的表面涂上颜色。小组活动红色:三个面涂色的
黄色:两个面涂色的
绿色:一个面涂色的列表的方法进行记录8000①②③④⑤812613.用棱长1 cm的小正方体拼成棱长为4cm的大正方体后,把它的表面涂上颜色。小组活动列表的方法进行记录8000①②③④⑤81261824248836542784896648000①②③④⑤81×12=121×1×6=61×1×1=182×12=242×2×6=242×2×2=883×12=363×3×6=543×3×3=2784×12=484×4×6=964×4×4=64观察上表,你能发现什么?在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。没有涂色的块数与面有关,即(n-2)2,或用总块数-三面涂色的块数-两面涂色的块数-一面涂色的块数。或343-8-60-150=125(个)棱长是7厘米的正方体中三面涂色的有几块?两面涂色的有几块?一面涂色的有几块?没有涂色的有几块?三面涂色8个两面涂色:(7-2)×12=60(个)一面涂色:(7-2)2×6=150(个)没有涂色的:(7-2)3=125(个)你还能继续写出第⑥、⑦、⑧个大正方体中4类正方体的块数吗?1把棱长为1厘米的小正方体拼成棱长为n的大正方体后涂色,涂色面的规律:
(1)三面涂色的小正方体个数=正方体的顶点个数=8。
(2)两面涂色的小正方体个数=12×(n-2)。
(3)一面涂色的小正方体个数=6×(n-2)2。
(4)没有涂色的小正方体个数=(n-2)3。这节课你有什么收获?如果摆成下面的几何体你会数吗?第1个图形中小正方体的个数:1+(1+2)=4;第2个图形中小正方体的个数:1+(1+2)+(1+2+3)=10;第3个图形中小正方体的个数:
1+(1+2)+(1+2+3)+(1+2+3+4)=20。1
