五年级上册数学试题-一课一练-6.4组合图形的面积 冀教版(含答案)
文档属性
| 名称 | 五年级上册数学试题-一课一练-6.4组合图形的面积 冀教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 95.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览


文档简介
五年级上册数学一课一练-6.4组合图形的面积
一、单选题
1.如图所示
则图中阴影部分的面积为(?? )
A.?50π?????????????????????????????????????B.?75π?????????????????????????????????????C.?90π?????????????????????????????????????D.?85π
2.两个面积相等的正方形拼成一个长方形,拼接前后的面积(??? )。
A.?增大??????????????????????????????????B.?减少??????????????????????????????????C.?不变??????????????????????????????????D.?无法确定
3.如图中的阴影部分面积是(? )平方厘米
A.?144?????????????????????????????????????B.?72?????????????????????????????????????C.?18?????????????????????????????????????D.?无法确定
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(??? )
6.任何两个三角形都可以拼成一个四边形。
三、填空题
7.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.
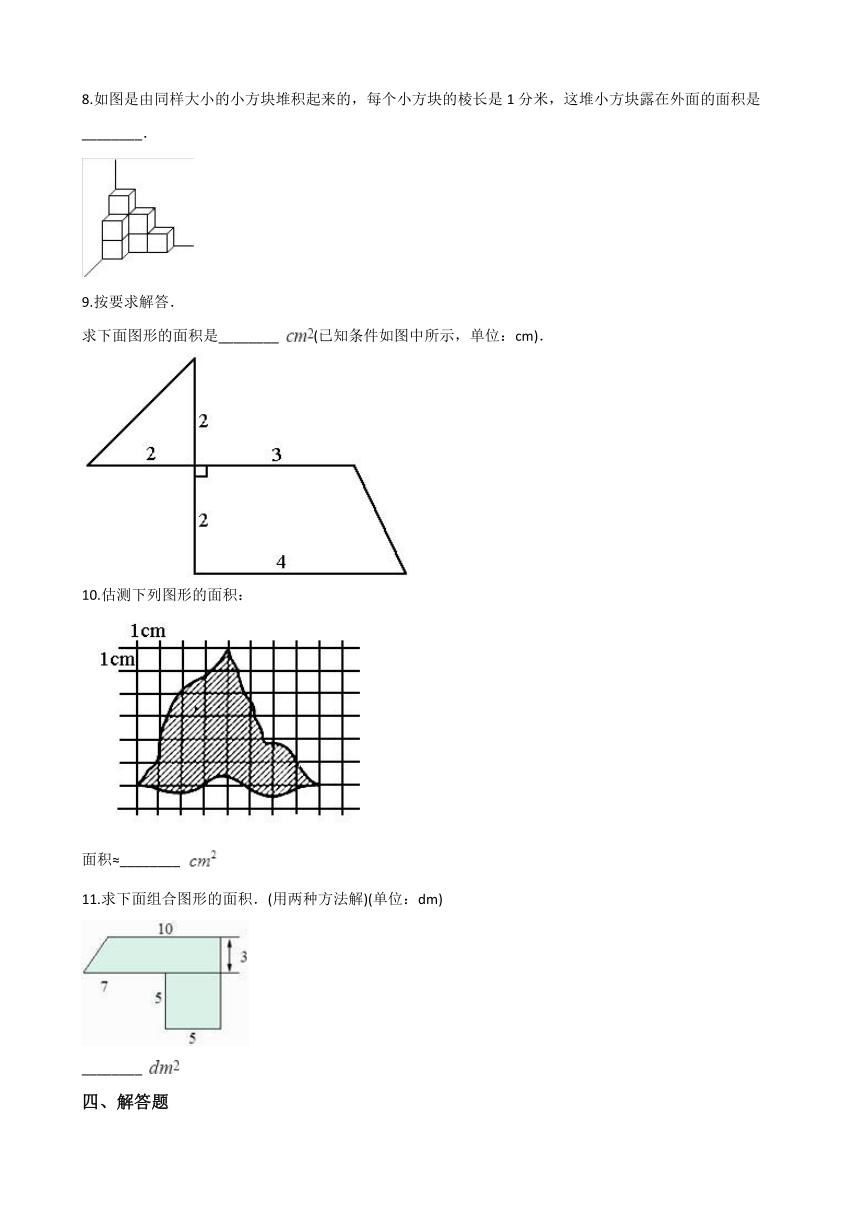
8.如图是由同样大小的小方块堆积起来的,每个小方块的棱长是1分米,这堆小方块露在外面的面积是________.
9.按要求解答. 求下面图形的面积是________ (已知条件如图中所示,单位:cm).
10.估测下列图形的面积:
面积≈________
11.求下面组合图形的面积.(用两种方法解)(单位:dm) ________
四、解答题
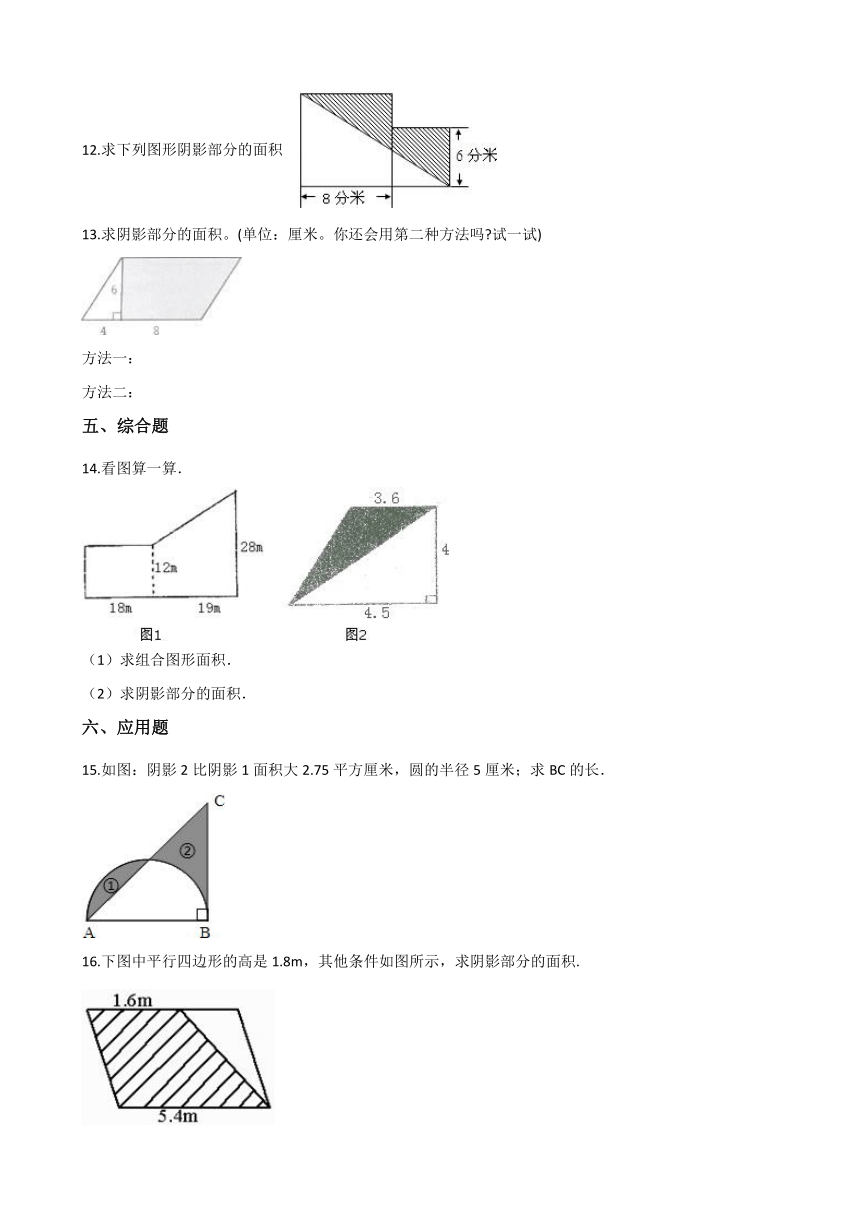
12.求下列图形阴影部分的面积
13.求阴影部分的面积。(单位:厘米。你还会用第二种方法吗?试一试) 方法一: 方法二:
五、综合题
14.看图算一算.
(1)求组合图形面积.
(2)求阴影部分的面积.
六、应用题
15.如图:阴影2比阴影1面积大2.75平方厘米,圆的半径5厘米;求BC的长.
16.下图中平行四边形的高是1.8m,其他条件如图所示,求阴影部分的面积.
参考答案
一、单选题
1.【答案】B
【解析】【解答】解:π×102-π×(10÷2)2
=100π-25π =75π(cm2) 故答案为:B 【分析】阴影部分的面积是大圆的面积减去小圆的面积,圆面积公式:S=πr2 , 根据圆面积公式计算即可.
2.【答案】 C
【解析】【解答】解:两个面积相等的正方形拼成一个长方形,拼接前后的面积不变。 故答案为:C。 【分析】两个面积相等的正方形拼成一个长方形后,这个长方形的面积就是这两个正方形面积。
3.【答案】 B
【解析】【解答】解:24×6÷2
=24×3
=72(平方厘米)
答:图中的阴影部分面积是72平方厘米.
故选:B.
【分析】阴影部分几个三角形的底的和正好等于长方形的长,高等于长方形的宽,所以阴影部分的面积是长方形面积的一半,根据长方形的面积公式S=ab解答即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。 故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】 正确
【解析】【解答】解:用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。 故答案为:正确。 【分析】用8个大小一样的正方形无论拼成什么图形,都是这8个正方形的面积,所以它们的面积都相等。
6.【答案】错误
【解析】【解答】如图所示, 上面的两个边长不等的等腰三角形只能组成五边形,不能组成一个四边形. 故答案为:错误。 【分析】三条边都不等,角不互补的三角形是不可能组成一个四边形的,据此判断。
三、填空题
7.【答案】30
【解析】【解答】解法一:5×5+5×2÷2 =25+10÷2 =25+5 解法二:(5+2+5)×(5÷2)÷2×2 =12×2.5 答:它的面积是 . 【分析】1.求组合图形的面积可以不写公式直接计算.2.计算组合图形的面积,要根据已知条件对图形进行分解,转化成会计算的简单图形的面积,分别计算出它们的面积,再求和.
8.【答案】15平方分米
【解析】【解答】解:根据题干分析可得: (4+6+5)×1×1=15(平方分米), 答:这堆小方块露在外面的面积是15平方分米. 故答案为:15平方分米. 【分析】从上面看,露出的小正方体的面有4个;从正面看,露出的小正方体的面有6个;从侧面看,露出的小正方体的面有5个;其它的三个面都被墙面和地面遮挡,由此即可求得这堆小正方形露在外面的面积.此题要注意是求露出来的表面积,所以这里的表面积是指只有三个面观察到的正方体的面的面积之和.
9.【答案】9
【解析】【解答】解:2×2÷2+(3+4)×2÷2 =2+7 =9(cm2) 故答案为:9 【分析】这个图形的面积是一个直角三角形面积加上一个直角梯形的面积,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2.
10.【答案】 24
【解析】【解答】解:面积≈24m2。 故答案为:24。
【分析】图中比半格小的忽略不计,比半格多,但不够整格的记作整格,2个半格是一个整格,据此作答即可。
11.【答案】58
【解析】【解答】(10+7十5)x3÷2+5x5=58平方分米。
【分析】梯形面积+正方形面积=组合图形面积
四、解答题
12.【答案】解:8×8+6×6﹣(8+6)×8÷2 =64+36﹣14×8÷2 =64+36﹣56 =44(平方分米) 答:阴影部分的面积是44平方分米
【解析】【分析】阴影部分的面积=大正方形的面积+小正方形的面积﹣空白三角形的面积,据此进行解答.
13.【答案】解:方法一: (4+8)×6-4×6÷2 =12×6-24÷2 =72-12 =60(平方厘米) 方法二: (8+4+8)×6÷2 =20×6÷2 =60(平方厘米) 答:阴影部分的面积是60平方厘米.
【解析】【分析】方法一:用平行四边形的面积减去空白部分三角形的面积就是阴影部分的面积;方法二:直接根据梯形的面积来计算阴影部分的面积即可.
五、综合题
14.【答案】 (1)解:18×12+(12+28)×19÷2
=216+380
=596(平方米)
答:组合图形的面积是596平方米
(2)解:3.6×4÷2
=3.6×2
=7.2
答:阴影部分的面积是7.2
【解析】【分析】(1)用长方形的面积加上梯形的面积就是组合图形的面积,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2.(2)阴影部分的面积直接用三角形的面积公式计算即可解答,三角形的面积=底×高÷2.此题主要考查的是梯形的面积公式(上底+下底)×高÷2、三角形的面积公式底×高÷2和长方形的面积公式的应用.
六、应用题
15.【答案】解:半圆面积为3.14×52× =39.25(平方厘米), 三角形ABC的面积为39.25+2.75=42(平方厘米), 所以BC=42×2÷(5×2), =84÷10, =8.4(厘米); 答:BC的长度是8.4厘米
【解析】【分析】从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知阴影2的面积比阴影1的面积大2.75平方厘米,故三角形ABC的面积比半圆面积大2.75平方厘米.半圆面积为3.14×52× =39.25(平方厘米),三角形ABC的面积为39.25+2.75=42(平方厘米),由此利用三角形的面积公式,即可求出BC的长度.此题考查了学生三角形以及圆的面积公式及其应用,同时考查了学生观察图形的能力.
16.【答案】解:(1.6+5.4)×1.8÷2=6.3
【解析】
一、单选题
1.如图所示
则图中阴影部分的面积为(?? )
A.?50π?????????????????????????????????????B.?75π?????????????????????????????????????C.?90π?????????????????????????????????????D.?85π
2.两个面积相等的正方形拼成一个长方形,拼接前后的面积(??? )。
A.?增大??????????????????????????????????B.?减少??????????????????????????????????C.?不变??????????????????????????????????D.?无法确定
3.如图中的阴影部分面积是(? )平方厘米
A.?144?????????????????????????????????????B.?72?????????????????????????????????????C.?18?????????????????????????????????????D.?无法确定
二、判断题
4.计算组合图形的面积也要用到基本图形的面积公式。
5.用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(??? )
6.任何两个三角形都可以拼成一个四边形。
三、填空题
7.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.
8.如图是由同样大小的小方块堆积起来的,每个小方块的棱长是1分米,这堆小方块露在外面的面积是________.
9.按要求解答. 求下面图形的面积是________ (已知条件如图中所示,单位:cm).
10.估测下列图形的面积:
面积≈________
11.求下面组合图形的面积.(用两种方法解)(单位:dm) ________
四、解答题
12.求下列图形阴影部分的面积
13.求阴影部分的面积。(单位:厘米。你还会用第二种方法吗?试一试) 方法一: 方法二:
五、综合题
14.看图算一算.
(1)求组合图形面积.
(2)求阴影部分的面积.
六、应用题
15.如图:阴影2比阴影1面积大2.75平方厘米,圆的半径5厘米;求BC的长.
16.下图中平行四边形的高是1.8m,其他条件如图所示,求阴影部分的面积.
参考答案
一、单选题
1.【答案】B
【解析】【解答】解:π×102-π×(10÷2)2
=100π-25π =75π(cm2) 故答案为:B 【分析】阴影部分的面积是大圆的面积减去小圆的面积,圆面积公式:S=πr2 , 根据圆面积公式计算即可.
2.【答案】 C
【解析】【解答】解:两个面积相等的正方形拼成一个长方形,拼接前后的面积不变。 故答案为:C。 【分析】两个面积相等的正方形拼成一个长方形后,这个长方形的面积就是这两个正方形面积。
3.【答案】 B
【解析】【解答】解:24×6÷2
=24×3
=72(平方厘米)
答:图中的阴影部分面积是72平方厘米.
故选:B.
【分析】阴影部分几个三角形的底的和正好等于长方形的长,高等于长方形的宽,所以阴影部分的面积是长方形面积的一半,根据长方形的面积公式S=ab解答即可.
二、判断题
4.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。 故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
5.【答案】 正确
【解析】【解答】解:用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。 故答案为:正确。 【分析】用8个大小一样的正方形无论拼成什么图形,都是这8个正方形的面积,所以它们的面积都相等。
6.【答案】错误
【解析】【解答】如图所示, 上面的两个边长不等的等腰三角形只能组成五边形,不能组成一个四边形. 故答案为:错误。 【分析】三条边都不等,角不互补的三角形是不可能组成一个四边形的,据此判断。
三、填空题
7.【答案】30
【解析】【解答】解法一:5×5+5×2÷2 =25+10÷2 =25+5 解法二:(5+2+5)×(5÷2)÷2×2 =12×2.5 答:它的面积是 . 【分析】1.求组合图形的面积可以不写公式直接计算.2.计算组合图形的面积,要根据已知条件对图形进行分解,转化成会计算的简单图形的面积,分别计算出它们的面积,再求和.
8.【答案】15平方分米
【解析】【解答】解:根据题干分析可得: (4+6+5)×1×1=15(平方分米), 答:这堆小方块露在外面的面积是15平方分米. 故答案为:15平方分米. 【分析】从上面看,露出的小正方体的面有4个;从正面看,露出的小正方体的面有6个;从侧面看,露出的小正方体的面有5个;其它的三个面都被墙面和地面遮挡,由此即可求得这堆小正方形露在外面的面积.此题要注意是求露出来的表面积,所以这里的表面积是指只有三个面观察到的正方体的面的面积之和.
9.【答案】9
【解析】【解答】解:2×2÷2+(3+4)×2÷2 =2+7 =9(cm2) 故答案为:9 【分析】这个图形的面积是一个直角三角形面积加上一个直角梯形的面积,三角形面积=底×高÷2,梯形面积=(上底+下底)×高÷2.
10.【答案】 24
【解析】【解答】解:面积≈24m2。 故答案为:24。
【分析】图中比半格小的忽略不计,比半格多,但不够整格的记作整格,2个半格是一个整格,据此作答即可。
11.【答案】58
【解析】【解答】(10+7十5)x3÷2+5x5=58平方分米。
【分析】梯形面积+正方形面积=组合图形面积
四、解答题
12.【答案】解:8×8+6×6﹣(8+6)×8÷2 =64+36﹣14×8÷2 =64+36﹣56 =44(平方分米) 答:阴影部分的面积是44平方分米
【解析】【分析】阴影部分的面积=大正方形的面积+小正方形的面积﹣空白三角形的面积,据此进行解答.
13.【答案】解:方法一: (4+8)×6-4×6÷2 =12×6-24÷2 =72-12 =60(平方厘米) 方法二: (8+4+8)×6÷2 =20×6÷2 =60(平方厘米) 答:阴影部分的面积是60平方厘米.
【解析】【分析】方法一:用平行四边形的面积减去空白部分三角形的面积就是阴影部分的面积;方法二:直接根据梯形的面积来计算阴影部分的面积即可.
五、综合题
14.【答案】 (1)解:18×12+(12+28)×19÷2
=216+380
=596(平方米)
答:组合图形的面积是596平方米
(2)解:3.6×4÷2
=3.6×2
=7.2
答:阴影部分的面积是7.2
【解析】【分析】(1)用长方形的面积加上梯形的面积就是组合图形的面积,长方形的面积=长×宽,梯形的面积=(上底+下底)×高÷2.(2)阴影部分的面积直接用三角形的面积公式计算即可解答,三角形的面积=底×高÷2.此题主要考查的是梯形的面积公式(上底+下底)×高÷2、三角形的面积公式底×高÷2和长方形的面积公式的应用.
六、应用题
15.【答案】解:半圆面积为3.14×52× =39.25(平方厘米), 三角形ABC的面积为39.25+2.75=42(平方厘米), 所以BC=42×2÷(5×2), =84÷10, =8.4(厘米); 答:BC的长度是8.4厘米
【解析】【分析】从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC的面积.又已知阴影2的面积比阴影1的面积大2.75平方厘米,故三角形ABC的面积比半圆面积大2.75平方厘米.半圆面积为3.14×52× =39.25(平方厘米),三角形ABC的面积为39.25+2.75=42(平方厘米),由此利用三角形的面积公式,即可求出BC的长度.此题考查了学生三角形以及圆的面积公式及其应用,同时考查了学生观察图形的能力.
16.【答案】解:(1.6+5.4)×1.8÷2=6.3
【解析】
