高中数学人教版必修5课件:2.4.1等比数列(共21张PPT)
文档属性
| 名称 | 高中数学人教版必修5课件:2.4.1等比数列(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
2.4.1 等比数列
Yesterday?once?more
1、定义:如果一个数列_____,每一项与它的前一项的差等于_____,这个数列就叫做等差数列。这个常数叫做等差数列的__,公差通常用字母_表示。
2、公差=___-___,即:____。
3、等差数列的通项公式:______。
从第2项起
同一个常数
公差
d
后项
前项
an-an-1=d
an=a1+(n-1)d
学习目标
1、掌握等比数列的定义,理解等比中项的概念;
2、掌握等比数列的通项公式及推导过程;
3、能利用等比数列的定义及通项公式解决问题。
重点:(1)等比数列概念的理解;
(2)等比数列通项公式的应用。
难点:等比数列通项公式的应用。
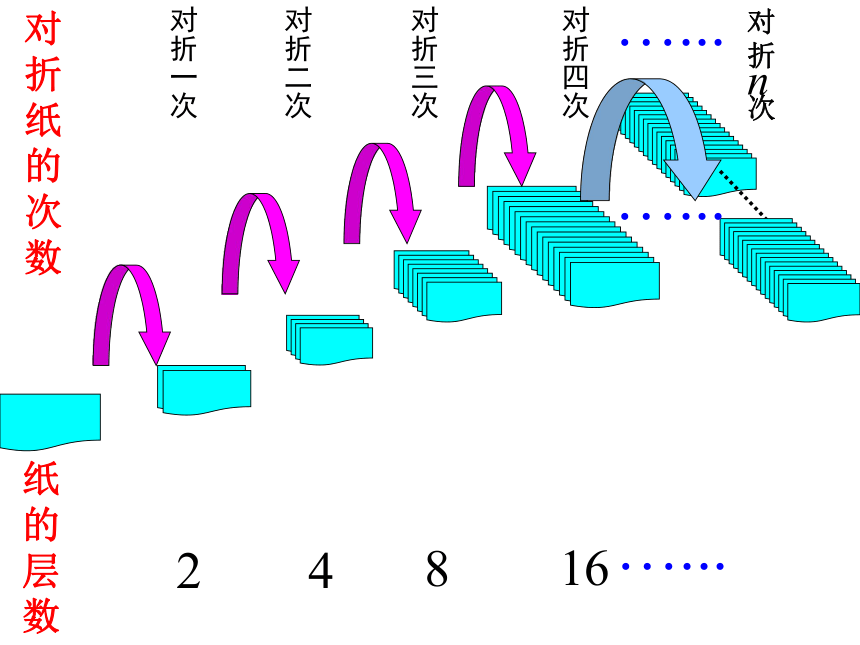
如果能将一张厚度为0.05mm的报纸对折,再对折,再对折‥‥‥依次对折50次,你相信这时报纸的厚度可以在地球和月球之间建一座桥?
情境一:折纸
对折一次
对折二次
对折三次
对折四次
…...
对折
次
对折纸的
次数
纸的层数
…...
…...
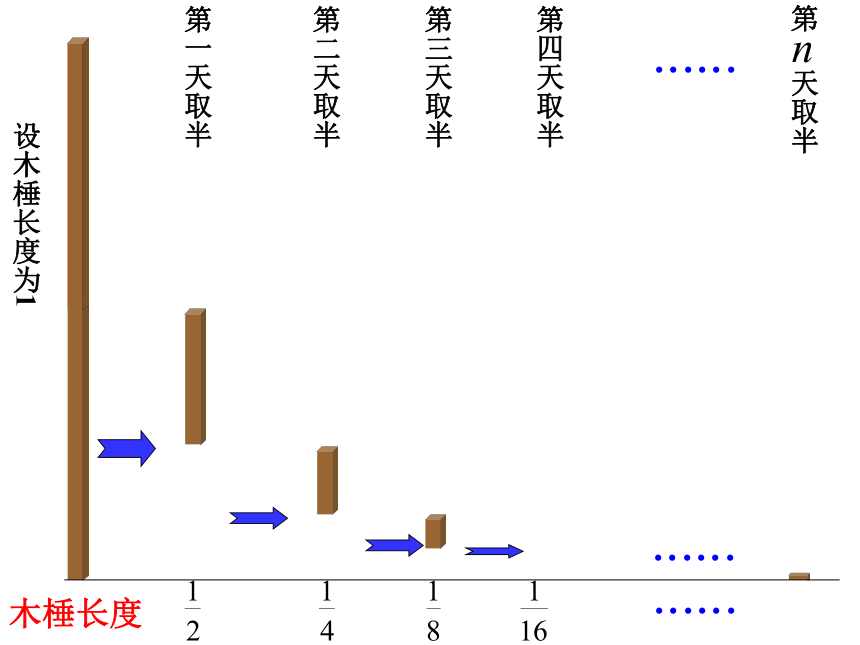
情境二:《庄子·天下篇》中写到:
“一尺之棰,日取其半,万世不竭”。
设木棰长度为1
木棰长度
第一天取半
第二天取半
第三天取半
第四天取半
......
......
......
第 天取半
观察这2个数列,看有何共同特点?
2, 4, 8, 16, …;
①②
共同特点:从第二项起,每一项与前一项
的比都等于同一个常数.
1、等比数列的定义:
一般地,如果一个数列从第2项起, 每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,
这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0)。
即: 或
(1)2,8,32,128,…
(2)-1,-0.5,-0.25,-0.125,…
(3)2,2,2,2,…
(4)1,-3,9,-27,…
(5)1,2,4,16,64,…
(6)1, 0, 1, 0, 1
q=4
q=1
q=-3
q=0.5
1、判断下列数列是否为等比数列,若是,请说出公比q。
√
×
√
√
√
概念辨析
×
1.等比数列要求从第2项起,后一项与前一项的比;
2.比值要求是同一个常数(q≠0);
3.等比数列每一项不可能是0.
抢答1:公比q的取值范围是什么呢?
抢答2:当公比q=1时的等比数列是什么样的数列?
抢答3:常数列一定是等差数列吗?一定是等比数列吗?为什么?
抢答4:既是等差数列,又是等比数列的数列存在吗?举例说明。
正数、负数,但是不能为零。
常数列
常数列都是等差数列,但却不一定都是等比数列。如数列0,0,0,0,…是等差不是等比数列。
先抢为快
2、等比数列中项:
与等差中项类似,如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
G=___。
自主学习(2min)
仿照“等差数列通项公式的推导”,完成任务:已知数列{an}是首项为a1,公比为q的等比数列,你能写出这个等比数列的第n项吗?
a1=a1
a2=a1 q
a3=a2 q=a1q2
a4=a3q=a1q3
…
an= .
不完全归纳法
3、等比数列的通项公式:
一般地,如果等比数列{an}的首项为a1,公比为q,则有:
an=a1qn-1
1.求等比数列1, 2,4,8,… 的通项公式.
求通项公式
2.在数列{an}中,a1=5,an=-5an+1,求通项公式.
3.求等比数列16, 8, 4,… 第8项
求指定项
5.在等比数列{an}中,已知a4=2,a7=16,求a1与q
求首项a1和公比q
4.在等比数列{an}中,已知a1=3,a3=27,求q
6.已知{an}为等比数列,若a1=
q= , an= , 则n=_ ;
求项数n
4
例已知数列{an}满足an=103n+5,证明数列{an}是等比数列。
注:要证明一个数列是等比数列,必须证明对任意的 都成立。
例题精讲
知识盘点
1、等比数列的定义:
2、等比中项:
3、等比数列的通项公式:
4、学习的思想方法:
an= a1qn-1
类比思想方法
课后作业
1.P53 A组第1(1)~(3)题
2.4.1 等比数列
Yesterday?once?more
1、定义:如果一个数列_____,每一项与它的前一项的差等于_____,这个数列就叫做等差数列。这个常数叫做等差数列的__,公差通常用字母_表示。
2、公差=___-___,即:____。
3、等差数列的通项公式:______。
从第2项起
同一个常数
公差
d
后项
前项
an-an-1=d
an=a1+(n-1)d
学习目标
1、掌握等比数列的定义,理解等比中项的概念;
2、掌握等比数列的通项公式及推导过程;
3、能利用等比数列的定义及通项公式解决问题。
重点:(1)等比数列概念的理解;
(2)等比数列通项公式的应用。
难点:等比数列通项公式的应用。
如果能将一张厚度为0.05mm的报纸对折,再对折,再对折‥‥‥依次对折50次,你相信这时报纸的厚度可以在地球和月球之间建一座桥?
情境一:折纸
对折一次
对折二次
对折三次
对折四次
…...
对折
次
对折纸的
次数
纸的层数
…...
…...
情境二:《庄子·天下篇》中写到:
“一尺之棰,日取其半,万世不竭”。
设木棰长度为1
木棰长度
第一天取半
第二天取半
第三天取半
第四天取半
......
......
......
第 天取半
观察这2个数列,看有何共同特点?
2, 4, 8, 16, …;
①②
共同特点:从第二项起,每一项与前一项
的比都等于同一个常数.
1、等比数列的定义:
一般地,如果一个数列从第2项起, 每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列,
这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0)。
即: 或
(1)2,8,32,128,…
(2)-1,-0.5,-0.25,-0.125,…
(3)2,2,2,2,…
(4)1,-3,9,-27,…
(5)1,2,4,16,64,…
(6)1, 0, 1, 0, 1
q=4
q=1
q=-3
q=0.5
1、判断下列数列是否为等比数列,若是,请说出公比q。
√
×
√
√
√
概念辨析
×
1.等比数列要求从第2项起,后一项与前一项的比;
2.比值要求是同一个常数(q≠0);
3.等比数列每一项不可能是0.
抢答1:公比q的取值范围是什么呢?
抢答2:当公比q=1时的等比数列是什么样的数列?
抢答3:常数列一定是等差数列吗?一定是等比数列吗?为什么?
抢答4:既是等差数列,又是等比数列的数列存在吗?举例说明。
正数、负数,但是不能为零。
常数列
常数列都是等差数列,但却不一定都是等比数列。如数列0,0,0,0,…是等差不是等比数列。
先抢为快
2、等比数列中项:
与等差中项类似,如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项。
G=___。
自主学习(2min)
仿照“等差数列通项公式的推导”,完成任务:已知数列{an}是首项为a1,公比为q的等比数列,你能写出这个等比数列的第n项吗?
a1=a1
a2=a1 q
a3=a2 q=a1q2
a4=a3q=a1q3
…
an= .
不完全归纳法
3、等比数列的通项公式:
一般地,如果等比数列{an}的首项为a1,公比为q,则有:
an=a1qn-1
1.求等比数列1, 2,4,8,… 的通项公式.
求通项公式
2.在数列{an}中,a1=5,an=-5an+1,求通项公式.
3.求等比数列16, 8, 4,… 第8项
求指定项
5.在等比数列{an}中,已知a4=2,a7=16,求a1与q
求首项a1和公比q
4.在等比数列{an}中,已知a1=3,a3=27,求q
6.已知{an}为等比数列,若a1=
q= , an= , 则n=_ ;
求项数n
4
例已知数列{an}满足an=103n+5,证明数列{an}是等比数列。
注:要证明一个数列是等比数列,必须证明对任意的 都成立。
例题精讲
知识盘点
1、等比数列的定义:
2、等比中项:
3、等比数列的通项公式:
4、学习的思想方法:
an= a1qn-1
类比思想方法
课后作业
1.P53 A组第1(1)~(3)题
