人教版高中数学必修4课件:2.1平面向量的实际背景及基本概念(共31张PPT)
文档属性
| 名称 | 人教版高中数学必修4课件:2.1平面向量的实际背景及基本概念(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 22:25:57 | ||
图片预览







文档简介
(共31张PPT)
向量最初被应用于物理学,被称为矢量.很多物理量,如力、速度、位移、电场强度、磁场强度等都是向量.
大约公元前350年,古希腊著名学者亚里士多德就知道了力可以表示为向量.向量一词来自力学、解析几何中的
有向线段.
最先使用有向线段表示向量的是
英国大科学家牛顿.
课前小知识
向量及向量符号的由来
三维目标
1.通过实例,利用平面向量的物理背景以及研究平面向量的必要性,理解平面向量的概念以及确定平面向量的两个要素,分清数量与向量的区别。
2.理解自由向量、平行向量、相等向量、相反向量等概念,并能判断它们之间的关系,并会辨认图形中的相等向量或作出与某一向量相等的向量。
3.在教学过程中,应充分根据平面向量的两个要素加以研究向量的关系,揭示向量可以平移这一特性。培养学生数形结合的思想。
重点难点
教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量;理解向量的大小及方向的表示及意义。
教学难点:向量、平行(共线)向量的概念。
课时安排:1课时
教学方法:类比归纳法、演示讨论法
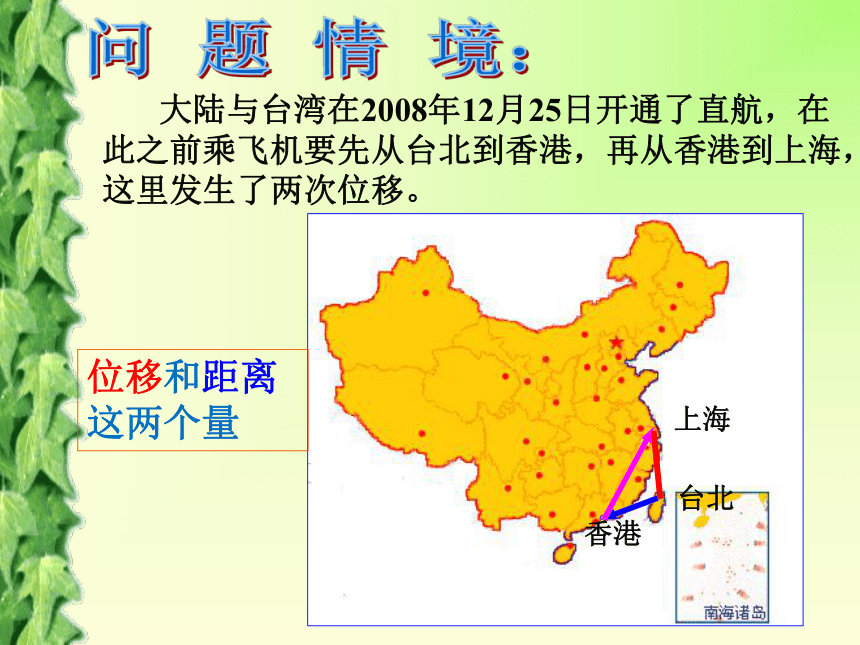
大陆与台湾在2008年12月25日开通了直航,在此之前乘飞机要先从台北到香港,再从香港到上海,这里发生了两次位移。
台北
香港
上海
位移和距离这两个量
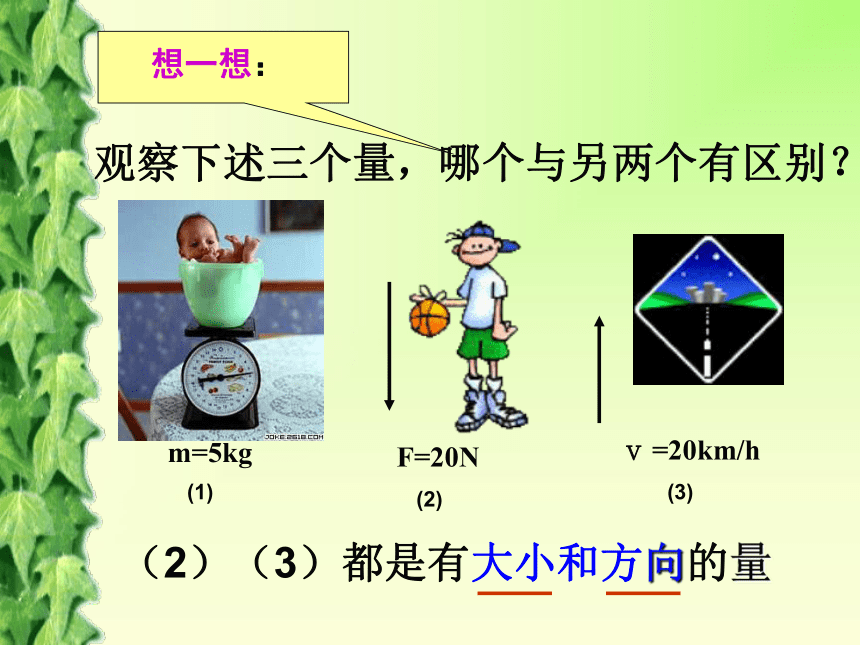
F=20N
v =20km/h
(2)(3)都是有大小和方向的量
m=5kg
(1)
(2)
(3)
观察下述三个量,哪个与另两个有区别?
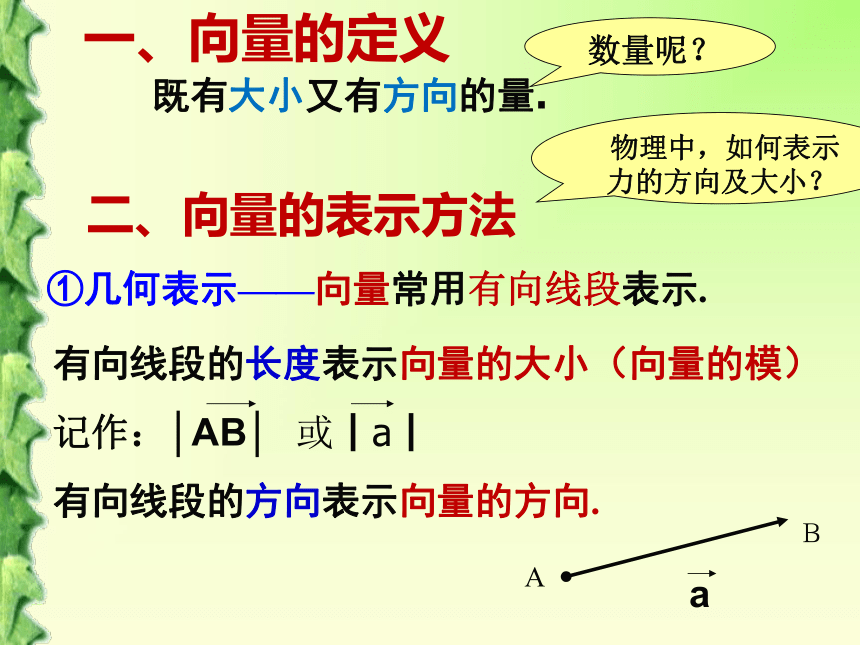
一、向量的定义
既有大小又有方向的量.
二、向量的表示方法
①几何表示——向量常用有向线段表示.
有向线段的长度表示向量的大小(向量的模)
记作:│AB│
有向线段的方向表示向量的方向.
物理中,如何表示力的方向及大小?
数量呢?
或以A为起点、B为终点的向量记为:AB.
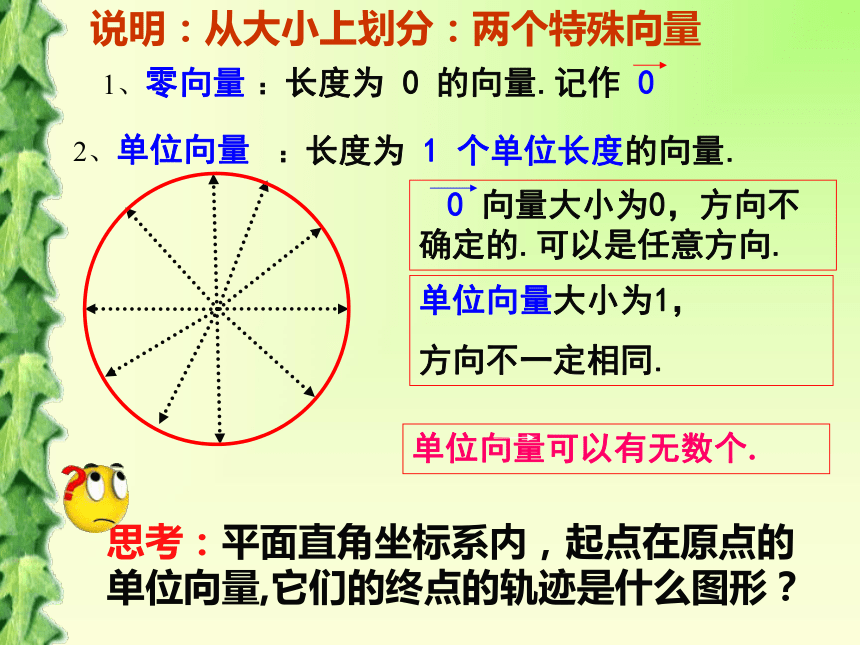
单位向量大小为1,
方向不一定相同.
:长度为 1 个单位长度的向量.
说明:从大小上划分:两个特殊向量
思考:平面直角坐标系内,起点在原点的
单位向量,它们的终点的轨迹是什么图形?
感悟:在物体运动教学中物理老师经常
比较拉力F与摩擦力f来分析物体的运动
状态,应该怎样理解?
注意:向量不能比较大小
三:向量之间的关系
1.平行向量的定义:
方向相同或相反的非零向量叫做平行向量.
我们规定零向量与任一向量平行.
两向量的平行与平面几何里两线段的平行
有什么区别?
也叫做共线向量
两向量的共线与平面几何里两线段的共线
是否一样?
(方向与大小)
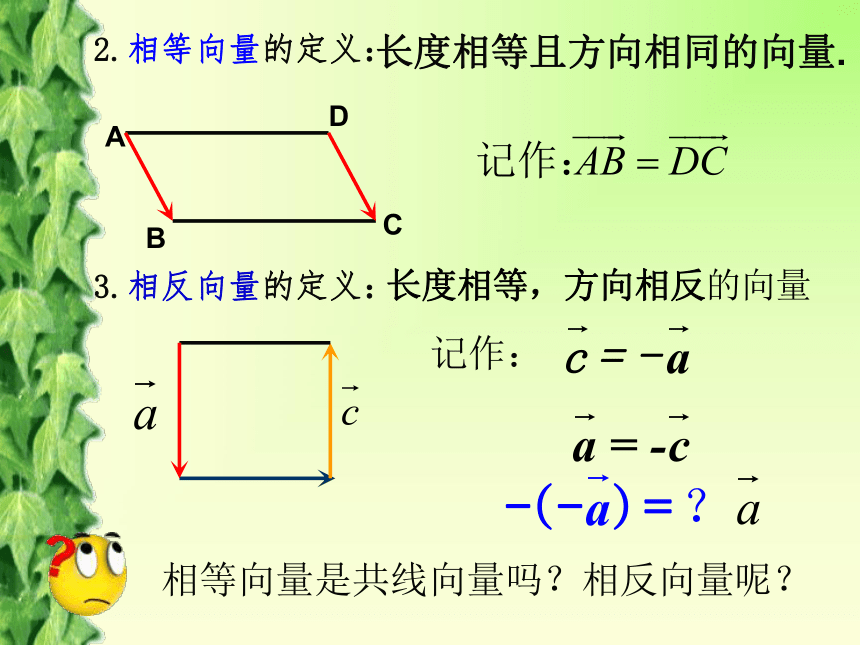
2.相等向量的定义:
长度相等且方向相同的向量.
3.相反向量的定义:
记作:
相等向量是共线向量吗?相反向量呢?
例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:
解:
热热身
分别以图中的格点为起点和终点作向量,
合作探究:
共有2种不同的模
共有8种不同的向量
★题:
★★★题:
1
2
3
4
5
6
7
8
9
10
11
★★题:
智勇大冲关
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
BACK
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
BACK
BACK
练习
1、与零向量相等的向量一定是什么向量?
2、与任意向量都平行的向量是什么向量?
BACK
练习
1、若两个向量在同一直线上,则这两个
向量是什么向量?
2、共线向量一定在一条直线上吗?
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等.
练习:
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
A
B
C
O
BACK
练习:
命题:“│a│=│b│”成立,则“ a = b ”一定成
立
BACK
练习:
1.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____
BACK
练习:
1.与非零向量 a (非单位向量)平行的向量中,不相等的单位向量有_____ 个.
2
练习:如图,EF是△ABC的中位线,AD是BC 边上的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。
A
B
C
D
E
F
BACK
7
5
2
如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
A
B
C
D
F
E
M
BACK
(1) 3个
(2) 9个
课堂小结
南辕北辙的故事
战国时,有个北方人要到南方的楚国去.
他从太行山脚下出发,乘着马车一直往
北走去.有人提醒他:“到楚国应该朝南走,
你怎能往北呢?”他却说:“不要紧,我有一
匹好马……”
结果: 原因:
板书设计:
2.1平面向量的实际背景
及基本概念
一、向量的定义 例题
二、向量的表示方法
三:向量之间的关系
教学反思:
向量最初被应用于物理学,被称为矢量.很多物理量,如力、速度、位移、电场强度、磁场强度等都是向量.
大约公元前350年,古希腊著名学者亚里士多德就知道了力可以表示为向量.向量一词来自力学、解析几何中的
有向线段.
最先使用有向线段表示向量的是
英国大科学家牛顿.
课前小知识
向量及向量符号的由来
三维目标
1.通过实例,利用平面向量的物理背景以及研究平面向量的必要性,理解平面向量的概念以及确定平面向量的两个要素,分清数量与向量的区别。
2.理解自由向量、平行向量、相等向量、相反向量等概念,并能判断它们之间的关系,并会辨认图形中的相等向量或作出与某一向量相等的向量。
3.在教学过程中,应充分根据平面向量的两个要素加以研究向量的关系,揭示向量可以平移这一特性。培养学生数形结合的思想。
重点难点
教学重点:理解并掌握向量、零向量、单位向量、相等向量、共线向量的概念,会表示向量;理解向量的大小及方向的表示及意义。
教学难点:向量、平行(共线)向量的概念。
课时安排:1课时
教学方法:类比归纳法、演示讨论法
大陆与台湾在2008年12月25日开通了直航,在此之前乘飞机要先从台北到香港,再从香港到上海,这里发生了两次位移。
台北
香港
上海
位移和距离这两个量
F=20N
v =20km/h
(2)(3)都是有大小和方向的量
m=5kg
(1)
(2)
(3)
观察下述三个量,哪个与另两个有区别?
一、向量的定义
既有大小又有方向的量.
二、向量的表示方法
①几何表示——向量常用有向线段表示.
有向线段的长度表示向量的大小(向量的模)
记作:│AB│
有向线段的方向表示向量的方向.
物理中,如何表示力的方向及大小?
数量呢?
或以A为起点、B为终点的向量记为:AB.
单位向量大小为1,
方向不一定相同.
:长度为 1 个单位长度的向量.
说明:从大小上划分:两个特殊向量
思考:平面直角坐标系内,起点在原点的
单位向量,它们的终点的轨迹是什么图形?
感悟:在物体运动教学中物理老师经常
比较拉力F与摩擦力f来分析物体的运动
状态,应该怎样理解?
注意:向量不能比较大小
三:向量之间的关系
1.平行向量的定义:
方向相同或相反的非零向量叫做平行向量.
我们规定零向量与任一向量平行.
两向量的平行与平面几何里两线段的平行
有什么区别?
也叫做共线向量
两向量的共线与平面几何里两线段的共线
是否一样?
(方向与大小)
2.相等向量的定义:
长度相等且方向相同的向量.
3.相反向量的定义:
记作:
相等向量是共线向量吗?相反向量呢?
例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:
解:
热热身
分别以图中的格点为起点和终点作向量,
合作探究:
共有2种不同的模
共有8种不同的向量
★题:
★★★题:
1
2
3
4
5
6
7
8
9
10
11
★★题:
智勇大冲关
练习:
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?
BACK
练习:
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?
BACK
BACK
练习
1、与零向量相等的向量一定是什么向量?
2、与任意向量都平行的向量是什么向量?
BACK
练习
1、若两个向量在同一直线上,则这两个
向量是什么向量?
2、共线向量一定在一条直线上吗?
在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等.
练习:
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
A
B
C
O
BACK
练习:
命题:“│a│=│b│”成立,则“ a = b ”一定成
立
BACK
练习:
1.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____
BACK
练习:
1.与非零向量 a (非单位向量)平行的向量中,不相等的单位向量有_____ 个.
2
练习:如图,EF是△ABC的中位线,AD是BC 边上的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。
A
B
C
D
E
F
BACK
7
5
2
如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
A
B
C
D
F
E
M
BACK
(1) 3个
(2) 9个
课堂小结
南辕北辙的故事
战国时,有个北方人要到南方的楚国去.
他从太行山脚下出发,乘着马车一直往
北走去.有人提醒他:“到楚国应该朝南走,
你怎能往北呢?”他却说:“不要紧,我有一
匹好马……”
结果: 原因:
板书设计:
2.1平面向量的实际背景
及基本概念
一、向量的定义 例题
二、向量的表示方法
三:向量之间的关系
教学反思:
