湘教版数学八年级上册第二章2.6用尺规作三角形同步练习题(含答案)
文档属性
| 名称 | 湘教版数学八年级上册第二章2.6用尺规作三角形同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-22 15:59:41 | ||
图片预览

文档简介
第二章2.6用尺规作全等三角形同步练习题(含答案)
姓名:__________ 班级:__________考号:__________
一、单选题(共10题;共30分)
1.用尺规作图,不能作出唯一直角三角形的是(? )
A.?已知两条直角边??????????????????????????????????????????????????B.?已知两个锐角
C.?已知一直角边和直角边所对的一锐角??????????????????D.?已知斜边和一直角边
2.下列四种基本尺规作图分别表示:①作一个角等于已知角;②作一个角的平分线;③作一条线段的垂直平分线;④过直线外一点P作已知直线的垂线。则对应作法错误的是(??? )
A.?? ①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
3.用直尺和圆规作一个角等于已知角,其依据是(?? )
A.?SSS?????????????????????????????????????B.?SAS?????????????????????????????????????C.?ASA?????????????????????????????????????D.?AAS
4.如图,点C在∠AOB的OB边上,用尺规作出了CN∥OA,作图痕迹中, 是(??? )
A.?以点C为圆心,OD为半径的弧???????????????B.?以点C为圆心,DM为半径的弧
C.?以点E为圆心,OD为半径的弧????????????????D.?以点E为圆心,DM为半径的弧
5.如图,已知线段AB,分别以点A、点B为圆心,以大于AB的长为半径画弧,
两弧交于点C和点D,作直线CD,在CD上取两点P、M,连接PA、PB、MA、MB,
则下列结论一定正确的是( )
A.?PA=MA B.?MA=PE C.?PE=BE D.?PA=PB
6.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求。连结AC,BC,
AD,BD,根据她的作图方法可知,四边形ADBC定是(??? )
A.?矩形???????????????????B.?正方形??????????????????C.?菱形?????????????????D.?平行四边形
7.已知两角及夹边作三角形,所用的基本作图方法是( )
A.?作已知角的平分线??????????????????????????????????????????????B.?作已知线段的垂直平分线
C.?过一点作已知直线的高???????????????????????????????????????D.?作一个角等于已知角和作一条线段等于已知线段
8.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为( )
A.?20 B.?22 C.?14 D.?16
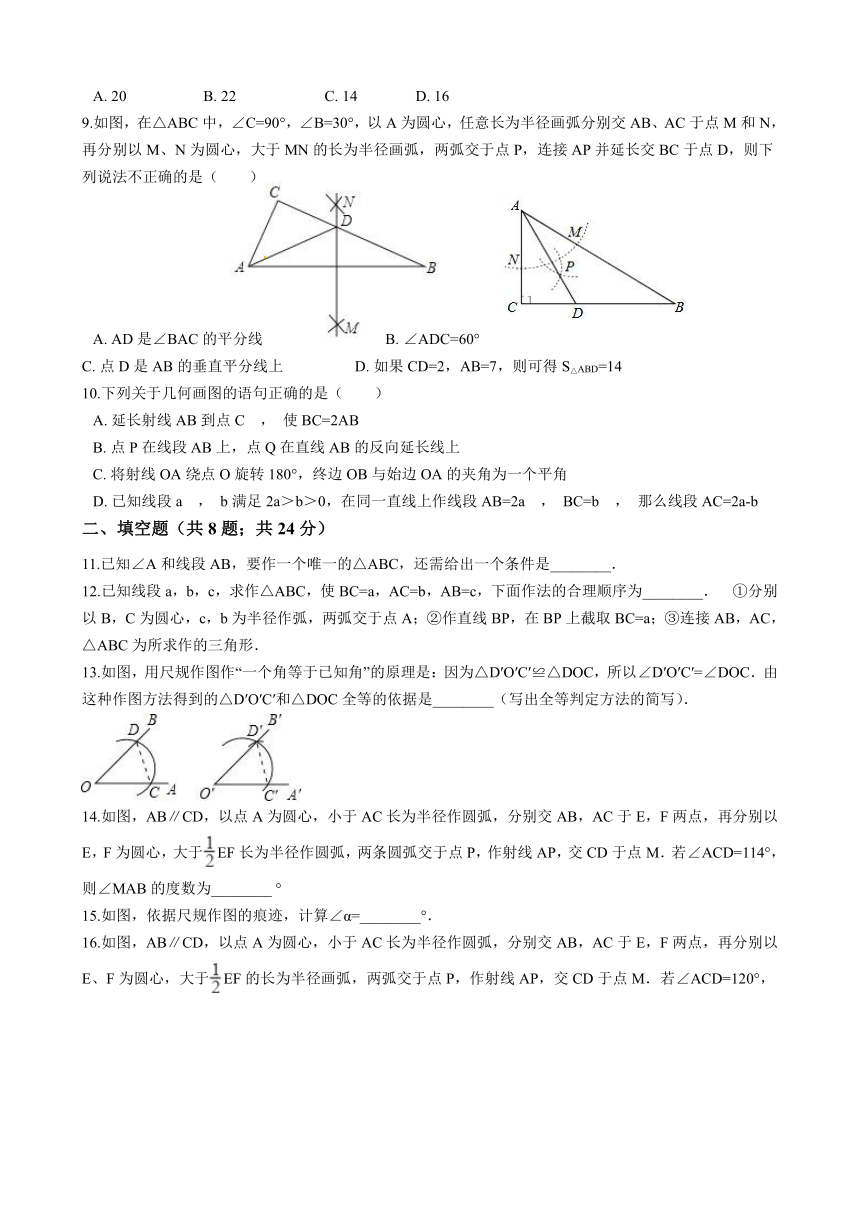
9.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法不正确的是( )
A.?AD是∠BAC的平分线 B.?∠ADC=60°
C.?点D是AB的垂直平分线上 D.?如果CD=2,AB=7,则可得S△ABD=14
10.下列关于几何画图的语句正确的是( )
A.?延长射线AB到点C , 使BC=2AB
B.?点P在线段AB上,点Q在直线AB的反向延长线上
C.?将射线OA绕点O旋转180°,终边OB与始边OA的夹角为一个平角
D.?已知线段a , b满足2a>b>0,在同一直线上作线段AB=2a , BC=b , 那么线段AC=2a-b
二、填空题(共8题;共24分)
11.已知∠A和线段AB,要作一个唯一的△ABC,还需给出一个条件是________.
12.已知线段a,b,c,求作△ABC,使BC=a,AC=b,AB=c,下面作法的合理顺序为________. ①分别以B,C为圆心,c,b为半径作弧,两弧交于点A;②作直线BP,在BP上截取BC=a;③连接AB,AC,△ABC为所求作的三角形.
13.如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′=∠DOC.由这种作图方法得到的△D′O′C′和△DOC全等的依据是________(写出全等判定方法的简写).
14.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.若∠ACD=114°,则∠MAB的度数为________?°
15.如图,依据尺规作图的痕迹,计算∠α=________°.
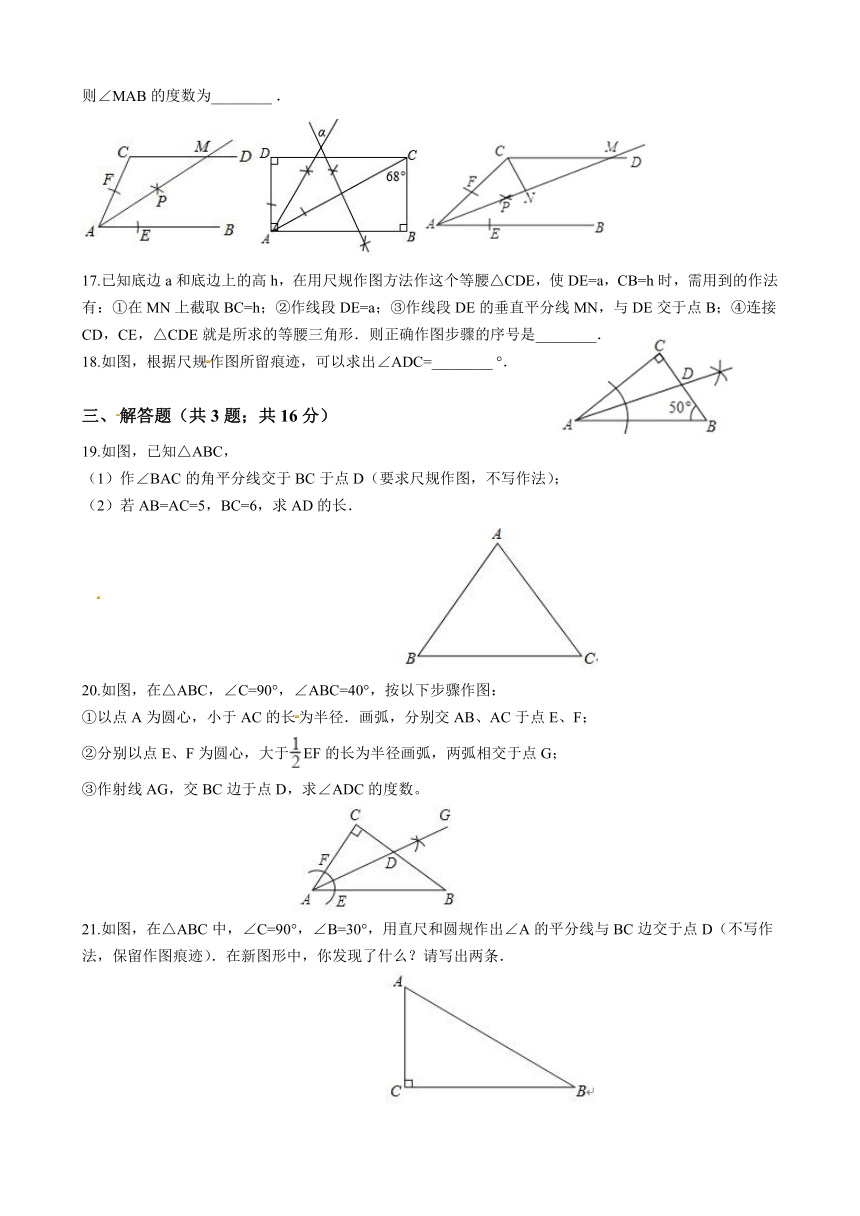
16.如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E、F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP,交CD于点M.若∠ACD=120°,则∠MAB的度数为________?.
17.已知底边a和底边上的高h,在用尺规作图方法作这个等腰△CDE,使DE=a,CB=h时,需用到的作法有:①在MN上截取BC=h;②作线段DE=a;③作线段DE的垂直平分线MN,与DE交于点B;④连接CD,CE,△CDE就是所求的等腰三角形.则正确作图步骤的序号是________.
18.如图,根据尺规作图所留痕迹,可以求出∠ADC=________?°.
三、解答题(共3题;共16分)
19.如图,已知△ABC,
(1)作∠BAC的角平分线交于BC于点D(要求尺规作图,不写作法);
(2)若AB=AC=5,BC=6,求AD的长.
20.如图,在△ABC,∠C=90°,∠ABC=40°,按以下步骤作图:
①以点A为圆心,小于AC的长为半径.画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于EF的长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D,求∠ADC的度数。
21.如图,在△ABC中,∠C=90°,∠B=30°,用直尺和圆规作出∠A的平分线与BC边交于点D(不写作法,保留作图痕迹).在新图形中,你发现了什么?请写出两条.
四、综合题(共6题;共50分)
22.如图,已知△ABC;(1)利用尺规作图:①在边AC下方作∠CAE=∠ACB;
②在射线AE上截取AD=BC;③连结CD,记CD交AB于点G.(尺规作图要求保留作图痕迹.不写作法)
(2)请写出按要求作图后所有全等的三角形:________.
23.正方形通过剪切可以拼成三角形,方法如下:
仿上用图示的方法,解答下列问题,操作设计
(1)对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的矩形;
(2)对任意三角形,设计一种方案,将它分若干块,再拼成一个与原三角形等面积的矩形.
24.如图所示,已知四点A、B、C、D. (1)画线段AB,射线AD,直线AC;(2)连接BD,BD与直线AC交于点E;(3)连接BC并延长线段BC与射线AD交于点F.
25.如图,已知 .
(1)用尺规作BC边的垂直平分线MN;
(2)在 的条件下,设MN与BC交于点D,与AC交于点E,连结BE,若 ,求 的度数
26.如图,在7×7的正方形网格中,每个小正方形的边长都为1个单位长度,△ABC的顶点都在正方形网格的格点上.①画出△ABC的AC边上的中线BD.②画出△ABC的BC边上的高线h.
③试在图中画出格点P,使得△PBC的面积与△ABC的面积相等,且△PBC为直角三角形.
27.综合题:(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.
(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)
(3)若AB=10,CD=3,求△ABD的面积.
答案
一、单选题
1.B 2.C 3.A 4.D 5.D 6.C 7.D 8.C 9.D 10.C
二、填空题
11.已知AC(或∠B) 12.②①③ 13.SSS 14.33 15.56 16.30° 17.②③①④ 18.70
三、解答题
19.解:(1)如图所示:AD即为所求;
(2)∵AB=AC=5,AD平分∠BAC,
∴AD⊥BC,且BD=DC=BC=3,
∴AD==4.
20.解:解法一:连接EF.
∵点E、F是以点A为圆心,小于AC的长为半径画弧,分别与AB、AC的交点,
∴AF=AE;
∴△AEF是等腰三角形;
又∵分别以点E、F为圆心,大于EF的长为半径画弧,两弧相交于点G;
∴AG是线段EF的垂直平分线,∴AG平分∠CAB,
∵∠ABC=40°∴∠CAB=50°,∴∠CAD=25°;
在△ADC中,∠C=90°,∠CAD=25°,
∴∠ADC=65°(直角三角形中的两个锐角互余);
解法二:根据已知条件中的作图步骤知,AG是∠CAB的平分线,
∵∠CAB=50°,∴∠CAD=25°;
在△ADC中,∠C=90°,∠CAD=25°,
∴∠ADC=65°(直角三角形中的两个锐角互余);
21.解:如图所示.
发现:∠CAB=60°,点D在AB的中垂线上.
∵∠C=90°,∠B=30°,
∴∠CAB=180°﹣90°﹣30°=60°,
∵AD平分∠CAB,∴∠DAB=?∠CAB=30°,
∴AD=BD,∴点D在AB的中垂线上.
四、综合题
22.(1)解:如图所示:
(2)△ACD≌△CAB、△ADG≌△CBG
23.(1)解:如图: (2)解:如图
24.(1)解:如图所示: (2)解:如图所示: (3)解:如图所示:
25.(1)解:如图所示:MN即为所求;
(2)解: 垂直平分BC,
,
,
,
26.解:①中线BD,即为所求:
②高线h,即为所求:
③点P1 , P2即为所求:
27.(1)证明:∵∠ACB=90?∴∠ACD+∠BCE=90?
∵ AD⊥l ∴∠ACD+∠CAD=90? ∴∠CAD=∠BCE
∵BE⊥l,AD⊥l
∴∠ADC=∠BEC=90?
∵AC=BC
∴△ACD≌△CBE
∴AD=CE,CD=BE
∵DE= CD+ CE
∴DE=AD+BE.
(2)
(3)解:过点D作DE⊥AB于E
∵DC⊥AC,DE⊥AB
∴DE=DC=3
∴
同课章节目录
