高中数学人教版必修1课件:2.2.1对数与对数运算(2)运算性质(共17张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:2.2.1对数与对数运算(2)运算性质(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 211.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 22:23:27 | ||
图片预览




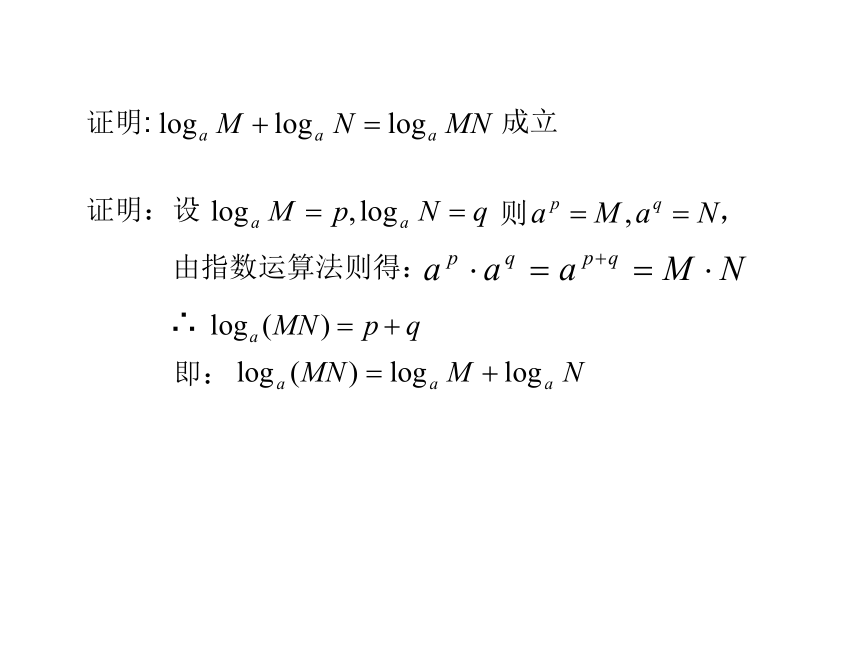
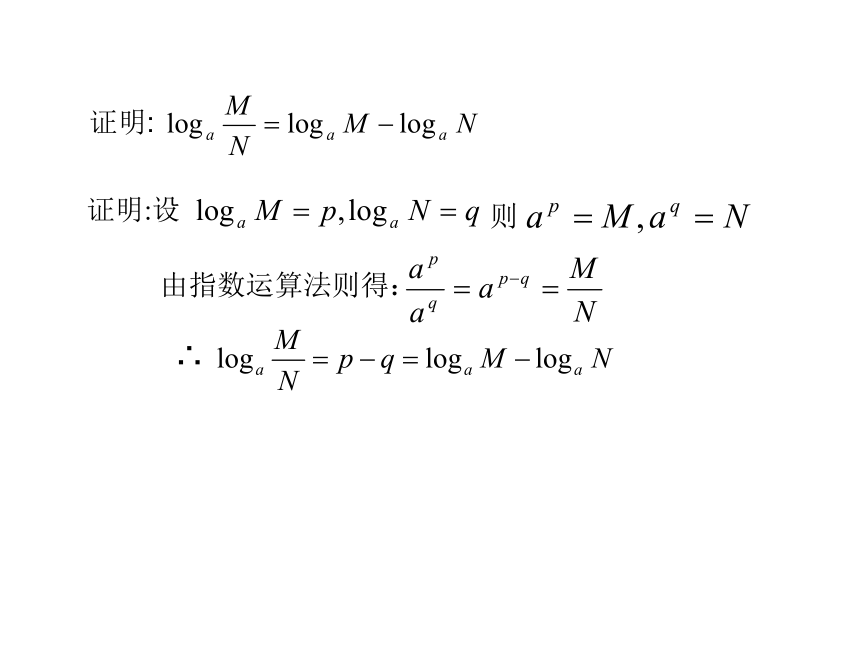

文档简介
(共17张PPT)
1.定义:一般地,如果
那么数 x叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
复习回顾
2.对数的基本性质:
① 零和负数没有对数.
② loga1=
③ logaa =
3.对数恒等式:
N
0
1
2.2.1对数与对数运算(2)
对数运算
学习目标:
1.掌握对数的运算性质。
2.能熟练运用运算性质解题。
重、难点:
对数的运算性质的理解与应用。
(1)
(2)
(3)
如果a>0,且a≠1,M>0,N>0 ,那么:
对数运算性质:
(自主学习P64~65,记忆对数运算性质)
两数积的对数,等于对数的和;
两数商的对数,等于对数的差;
幂的对数等于幂指数乘以底数的对数.
成立
证明:
由指数运算法则得:
证明:设
则
∴
即:
由指数运算法则得:
证明:设
则
∴
证明:
证明:
设
则
证明:
例1 用logax,logay,logaz表示下列各式:
; (2) .
例2 求下列各式的值:
(1)log2(47×25); (2) lg ;
公式逆用
例3 求下列各式的值:
仔细辨析啊!
你会做吗?
难度提升!
练习:
1.第68页,1,2,3.
小结:
(1)
(2)
(3)
如果a>0,且a≠1,M>0,N>0 ,那么:
对数运算性质:
作业:
1.P74习题2.2A组:3,4,5
2.系统作业.
计算(1)
答案(1)1;
(2)12;
(3) .
(2)已知 求 的值;
(3)已知 ,求 的值.
作业:
1.定义:一般地,如果
那么数 x叫做
以a为底 N的对数,记作
a叫做对数的底数,N叫做真数。
复习回顾
2.对数的基本性质:
① 零和负数没有对数.
② loga1=
③ logaa =
3.对数恒等式:
N
0
1
2.2.1对数与对数运算(2)
对数运算
学习目标:
1.掌握对数的运算性质。
2.能熟练运用运算性质解题。
重、难点:
对数的运算性质的理解与应用。
(1)
(2)
(3)
如果a>0,且a≠1,M>0,N>0 ,那么:
对数运算性质:
(自主学习P64~65,记忆对数运算性质)
两数积的对数,等于对数的和;
两数商的对数,等于对数的差;
幂的对数等于幂指数乘以底数的对数.
成立
证明:
由指数运算法则得:
证明:设
则
∴
即:
由指数运算法则得:
证明:设
则
∴
证明:
证明:
设
则
证明:
例1 用logax,logay,logaz表示下列各式:
; (2) .
例2 求下列各式的值:
(1)log2(47×25); (2) lg ;
公式逆用
例3 求下列各式的值:
仔细辨析啊!
你会做吗?
难度提升!
练习:
1.第68页,1,2,3.
小结:
(1)
(2)
(3)
如果a>0,且a≠1,M>0,N>0 ,那么:
对数运算性质:
作业:
1.P74习题2.2A组:3,4,5
2.系统作业.
计算(1)
答案(1)1;
(2)12;
(3) .
(2)已知 求 的值;
(3)已知 ,求 的值.
作业:
