高中数学人教版必修1课件:2.3幂函数(共16张PPT)
文档属性
| 名称 | 高中数学人教版必修1课件:2.3幂函数(共16张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 898.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
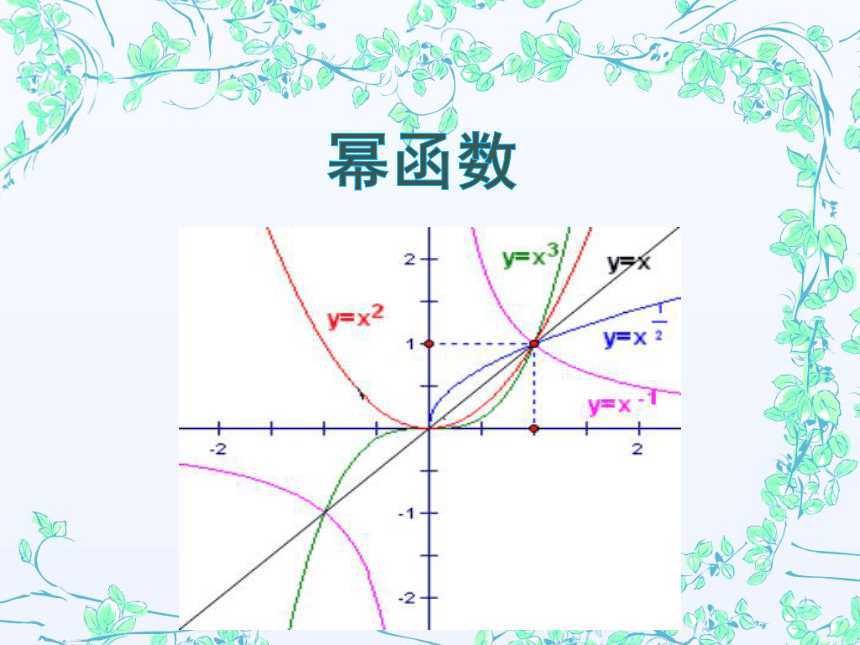
幂函数
1.通过实例了解幂函数的概念.
2.结合几个常见幂函数的图象发现幂函数的性质.
学习目标:
难点和重点:
学会数形结合的思想概括出幂函数的性质.
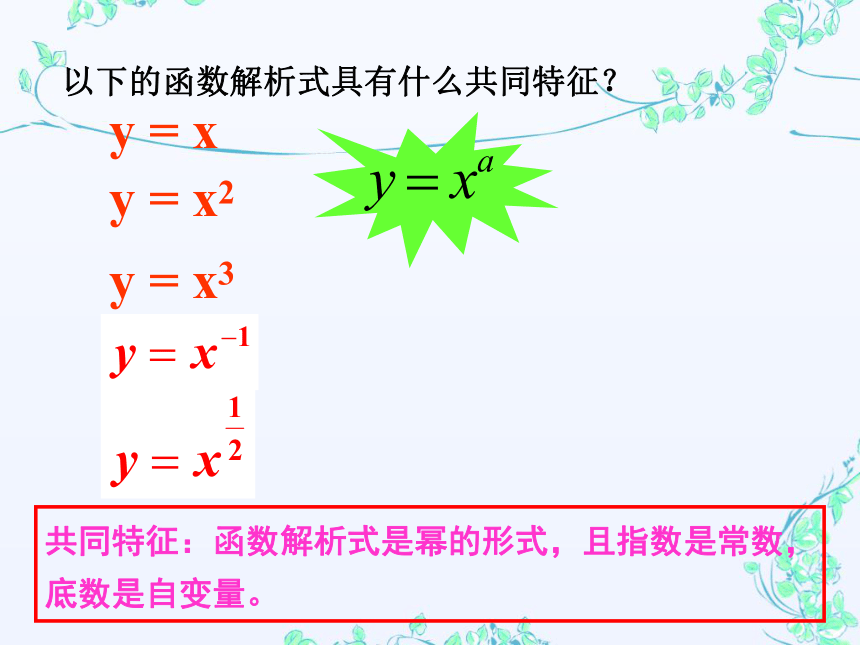
以下的函数解析式具有什么共同特征?
y = x3
y = x
y = x2
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。
一般地,函数 叫做幂函数,其中x为自变量,α为常数。
一、幂函数的概念
例:如果函数f (x) = (m2-m-1) 是幂函数,求实数m的值。
m= -1 或 m= 2
探究1:你能举几个学过的幂函数的例子吗?
探究2:幂函数与指数函数有什么区别?
1、下面几个函数中,哪几个函数是幂函数?
(1)y =
(2)y=2x2
(3)y=x2 + x
(4)
(5)y = 2x
概念辨析:
2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。
待定系数法
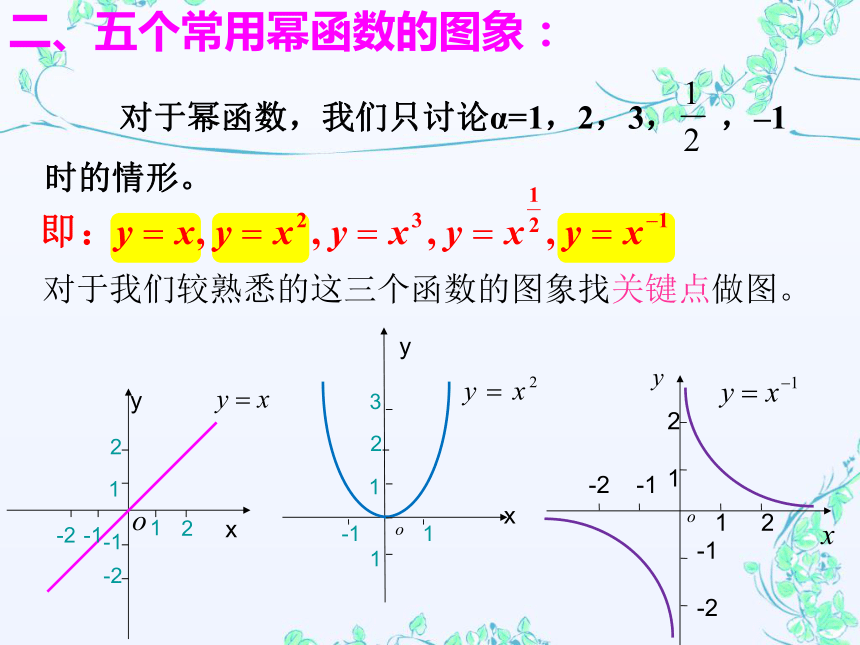
对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。
二、五个常用幂函数的图象:
1
2
-1
-2
1
2
-1
-2
1
1
2
3
1
-1
x
y
x
y
1 2
-2 -1
-1
-2
2
1
对于我们较熟悉的这三个函数的图象找关键点做图。
x … -2 -1 0 1 2 3 4 …
y=x3 … …
… …
-8
-1
0
1
8
27
0
1
0
x
y
1
2
3
4
-1
-2
-3
2
4
6
8
-2
-4
-6
-8
y=x3
/
/
64
y=
x
2
结合课本77页图2.3.1幂函数图象,将你发现的结论填在课本78页的表格内:
三、幂函数的性质:
y = x3
定义域
值 域
单调性
公共点
y = x
R
R
R
[0,+∞)
R
[0,+∞)
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非偶
奇函数
R上是增函数
在(-∞,0)上是减函数,
在(0, +∞)上是增函数
R上是增函数
在(0,+∞)上是增函数
在( -∞,0)和(0, +∞)上是减函数
(1,1)
奇偶性
y = x2
幂函数的性质:(定义域、奇偶性、单调性,因函数式中α的不同而各异)
1. 所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
3. 当α >0时,幂函数在区间(0,+∞)上是增函数;
当α<0时,幂函数在区间(0,+∞)上是减函数.
2. 当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数.
α<0
α>1
0<α<1
例1 利用单调性判断下列各值的大小。
(1)5.20.8 与 5.30.8
(2)0.2-0.3 与 0.3-0.3
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3
∴ 5.20.8 < 5.30.8
(2)y=x-0.3在(0,+∞)内是减函数
∵0.2<0.3
∴ 0.2-0.3>0.3-0.3
练习1.
(1)
(2)
(3)
(4)
<
<
>
>
2.若 ,则求m的取值范围.
3.幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系是( )
(A)a>b>c>d
(B)d>b>c>a
(C)d>c>b>a
(D)b>c>d>a
D
小结
1、幂函数的定义及图象特征?
2、幂函数的性质
(1)幂函数图象过定点(1,1)
(2)当α为奇数时,幂函数为奇函数;
当α为偶数时,幂函数为偶函数.
(3)当α>0时,在(0,+∞)上为增函数;
当α<0时,在(0,+∞)上为减函数。
幂函数
1.通过实例了解幂函数的概念.
2.结合几个常见幂函数的图象发现幂函数的性质.
学习目标:
难点和重点:
学会数形结合的思想概括出幂函数的性质.
以下的函数解析式具有什么共同特征?
y = x3
y = x
y = x2
共同特征:函数解析式是幂的形式,且指数是常数,底数是自变量。
一般地,函数 叫做幂函数,其中x为自变量,α为常数。
一、幂函数的概念
例:如果函数f (x) = (m2-m-1) 是幂函数,求实数m的值。
m= -1 或 m= 2
探究1:你能举几个学过的幂函数的例子吗?
探究2:幂函数与指数函数有什么区别?
1、下面几个函数中,哪几个函数是幂函数?
(1)y =
(2)y=2x2
(3)y=x2 + x
(4)
(5)y = 2x
概念辨析:
2、已知幂函数y = f (x)的图象经过点(3 , ),求这个函数的解析式。
待定系数法
对于幂函数,我们只讨论α=1,2,3, ,–1 时的情形。
二、五个常用幂函数的图象:
1
2
-1
-2
1
2
-1
-2
1
1
2
3
1
-1
x
y
x
y
1 2
-2 -1
-1
-2
2
1
对于我们较熟悉的这三个函数的图象找关键点做图。
x … -2 -1 0 1 2 3 4 …
y=x3 … …
… …
-8
-1
0
1
8
27
0
1
0
x
y
1
2
3
4
-1
-2
-3
2
4
6
8
-2
-4
-6
-8
y=x3
/
/
64
y=
x
2
结合课本77页图2.3.1幂函数图象,将你发现的结论填在课本78页的表格内:
三、幂函数的性质:
y = x3
定义域
值 域
单调性
公共点
y = x
R
R
R
[0,+∞)
R
[0,+∞)
R
[0,+∞)
奇函数
偶函数
奇函数
非奇非偶
奇函数
R上是增函数
在(-∞,0)上是减函数,
在(0, +∞)上是增函数
R上是增函数
在(0,+∞)上是增函数
在( -∞,0)和(0, +∞)上是减函数
(1,1)
奇偶性
y = x2
幂函数的性质:(定义域、奇偶性、单调性,因函数式中α的不同而各异)
1. 所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1);
3. 当α >0时,幂函数在区间(0,+∞)上是增函数;
当α<0时,幂函数在区间(0,+∞)上是减函数.
2. 当α为奇数时,幂函数为奇函数,
当α为偶数时,幂函数为偶函数.
α<0
α>1
0<α<1
例1 利用单调性判断下列各值的大小。
(1)5.20.8 与 5.30.8
(2)0.2-0.3 与 0.3-0.3
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3
∴ 5.20.8 < 5.30.8
(2)y=x-0.3在(0,+∞)内是减函数
∵0.2<0.3
∴ 0.2-0.3>0.3-0.3
练习1.
(1)
(2)
(3)
(4)
<
<
>
>
2.若 ,则求m的取值范围.
3.幂函数f(x)=xa ,f(x)=xb ,f(x)=xc, f(x)=xd,在第一象限的图象如图所示,则a,b,c,d的大小关系是( )
(A)a>b>c>d
(B)d>b>c>a
(C)d>c>b>a
(D)b>c>d>a
D
小结
1、幂函数的定义及图象特征?
2、幂函数的性质
(1)幂函数图象过定点(1,1)
(2)当α为奇数时,幂函数为奇函数;
当α为偶数时,幂函数为偶函数.
(3)当α>0时,在(0,+∞)上为增函数;
当α<0时,在(0,+∞)上为减函数。
