人教版九年级数第22章:一道二次函数题的经典30问 课件(共34张PPT 题目无答案)
文档属性
| 名称 | 人教版九年级数第22章:一道二次函数题的经典30问 课件(共34张PPT 题目无答案) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-28 12:33:42 | ||
图片预览




文档简介
(共34张PPT)
一道二次函数题的经典30问
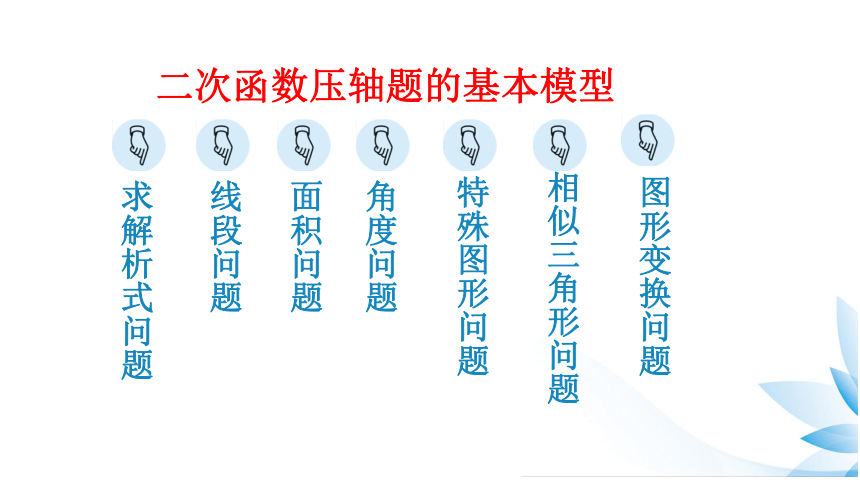
二次函数压轴题的基本模型
求解析式问题
线段问题
面积问题
特殊图形问题
相似三角形问题
角度问题
图形变换问题
题
目
呈
现
问
题
01
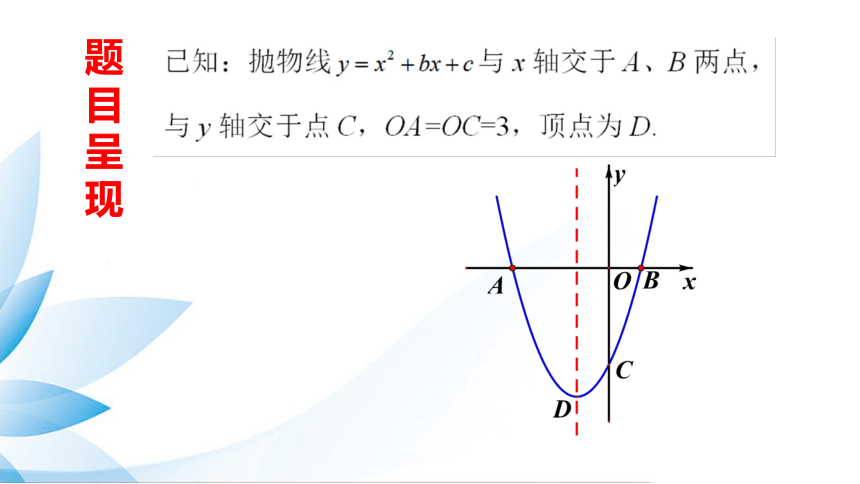
已知:抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.
(1)求此抛物线的解析式及点D的坐标.
y=x2+2x-3
D(-1,-4)
问
题
02
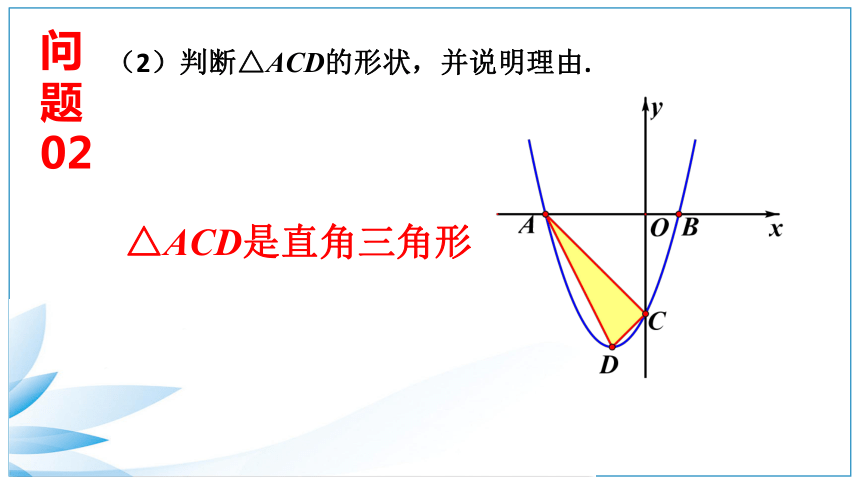
(2)判断△ACD的形状,并说明理由.
△ACD是直角三角形
问
题
03
(3)求四边形ABCD的面积.
问
题
04
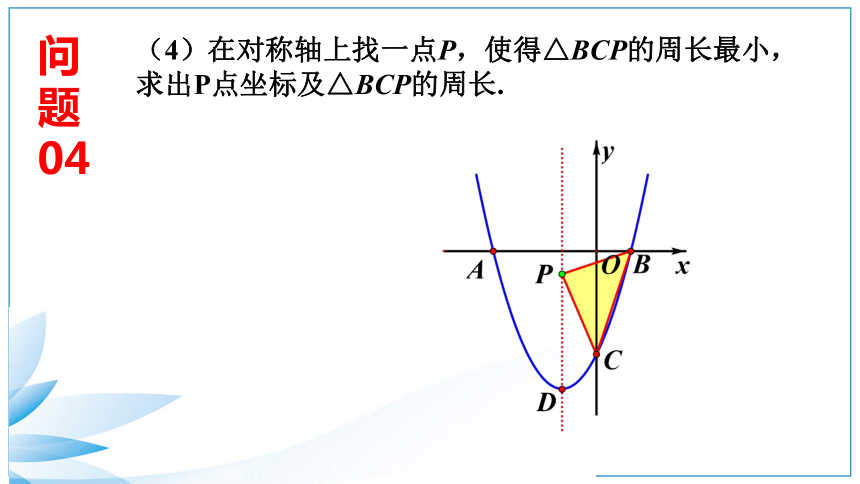
(4)在对称轴上找一点P,使得△BCP的周长最小,求出P点坐标及△BCP的周长.
问
题
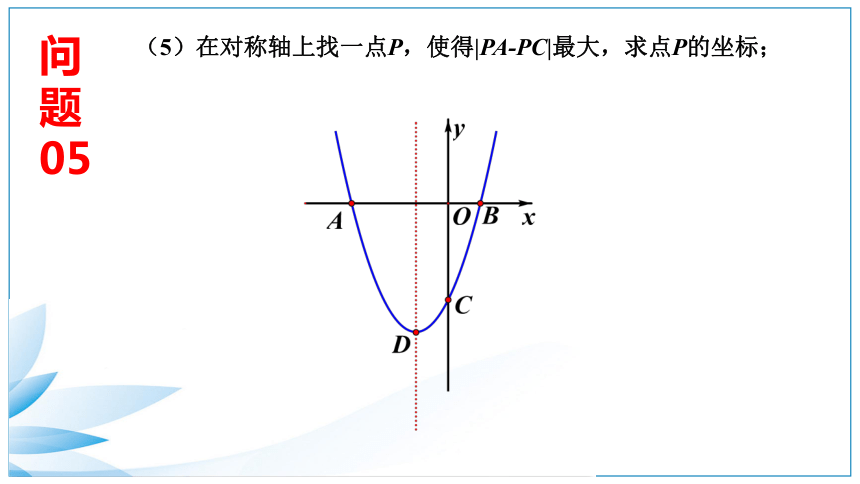
05
(5)在对称轴上找一点P,使得|PA-PC|最大,求点P的坐标;
问
题
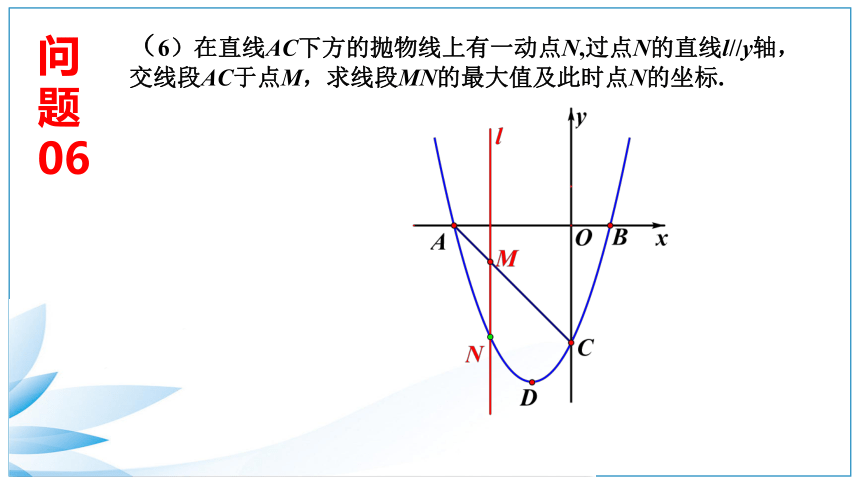
06
(6)在直线AC下方的抛物线上有一动点N,过点N的直线l//y轴,交线段AC于点M,求线段MN的最大值及此时点N的坐标.
问
题
07
(7)E是y轴上一动点,若BE=CE, 求点E的坐标.
问
题
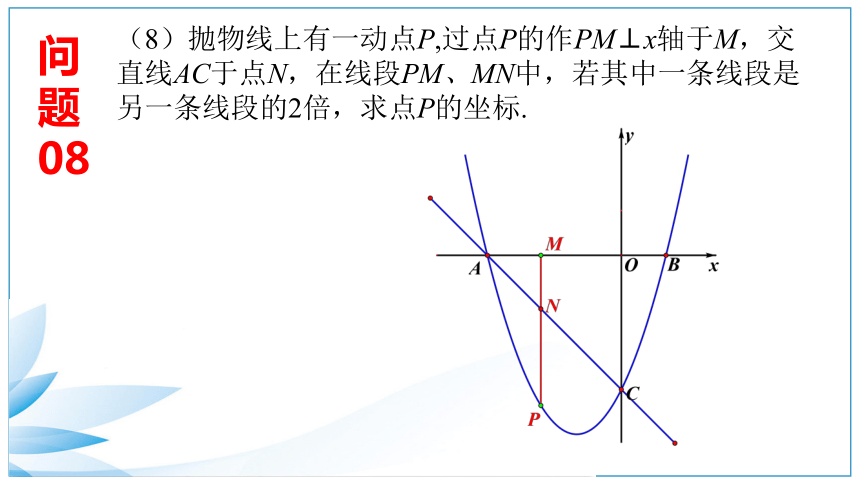
08
(8)抛物线上有一动点P,过点P的作PM⊥x轴于M,交直线AC于点N,在线段PM、MN中,若其中一条线段是另一条线段的2倍,求点P的坐标.
问
题
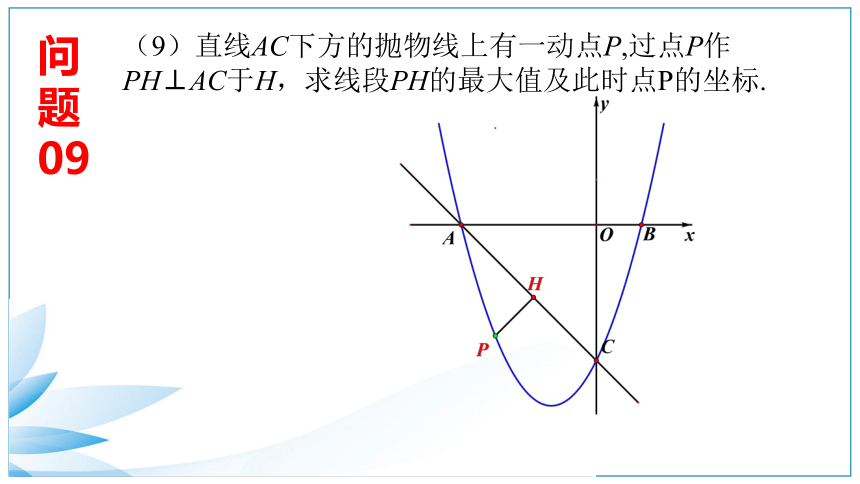
09
(9)直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,求线段PH的最大值及此时点P的坐标.
问
题
10
(10)直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,PG//y轴交AC于G,以GH、PH为邻边作矩形PEGH,求矩形PEGH
周长的最小值.
问
题
11
(11)在AC下方的抛物线上是否存在一点N,使得△CAN的面积最大?若存在,请求出△CAN的最大面积及点N的坐标.
问
题
12
(12)在AC下方的抛物线上是否存在一点N,使得四边形ABCN的面积最大?若存在,请求出四边形ABCN的最大面积
问
题
13
(13)在y轴上是否存在一点E,使得△ADE是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由;
问
题
14
(14)在y轴上是否存在一点F,使得△ADF是等腰三角形?若存在,求出点F的坐标;若不存在,请说明理由.
问
题
15
(15)抛物线上是否存在一点N(不与点C重合),使得 ?若存在,求出点N的坐标;若不存在,请说明理由;
问
题
16
(16)抛物线上是否存在一点H,使得 ?
若存在,求出点H的坐标;若不存在,请说明理由;
问
题
17
(17)抛物线上是否存在一点Q,使得 ?
若存在,求出点Q的坐标;若不存在,请说明理由;
问
题
18
(18)抛物线上是否存在一点E,使得BE平分△ABC的面积?若存在,求出点E的坐标;若不存在,请说明理由.
问
题
19
(19)抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC平分△APM的面积.
问
题
20
(20)抛物线上找一点P,作PM⊥x轴,交线段AC于点H,使AC分△APM的面积为2:1两部分.
问
题
21
(21)在对称轴上有一点M,在抛物线上有一点N,若以A、B、M、N为顶点的四边形是平行四边形,求M、N的坐标;
问
题
22
(22)作垂直于x的直线x=-1, 交直线AC于点M,交抛物线于点N,以A、M、N、E为顶点作平行四边形,求第四个顶点E的坐标;
问
题
23
(23)点E是抛物线上一动点,点F在抛物线的对称轴上,若以C、D、E、F为顶点的四边形是菱形,求点E的坐标.
问
题
24
(24)在抛物线上能不能找到一点P,使得∠POC=∠PCO 若能,求出点P的坐标;若不能,请说明理由.
问
题
25
(25)在线段AC上是否存在点M,使得△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由;
问
题
26
(26)P是抛物线上一个动点,作PH⊥x轴于H,是否存在一点P,使得△PAH与△BOC相似 若存在,求出点P的坐标,说明理由.
问
题
27
(27)将△BOC绕平面内一点顺时针旋转90°,得到△B'O'P', 若△B'O'P'恰好有两个点同时落在抛物线上,求点O'的横坐标.
问
题
28
(28)将AD所在直线绕点A逆时针旋转45°,所得直线与抛物线交于点M,求点M的坐标.
问
题
29
(29)过点B的直线交直线AC于点M, 当直线AC与BM的夹角等于∠ACB的2倍时,直接写出点M的坐标.
问
题
30
(30)y轴上是否存在一点N, 使得∠BCO+∠BNO=∠BAC 若存在,直接写出点N的坐标.
演示完毕 感谢聆听
THANKS
一道二次函数题的经典30问
二次函数压轴题的基本模型
求解析式问题
线段问题
面积问题
特殊图形问题
相似三角形问题
角度问题
图形变换问题
题
目
呈
现
问
题
01
已知:抛物线 与x轴交于A、B两点,与y轴交于点C,OA=OC=3,顶点为D.
(1)求此抛物线的解析式及点D的坐标.
y=x2+2x-3
D(-1,-4)
问
题
02
(2)判断△ACD的形状,并说明理由.
△ACD是直角三角形
问
题
03
(3)求四边形ABCD的面积.
问
题
04
(4)在对称轴上找一点P,使得△BCP的周长最小,求出P点坐标及△BCP的周长.
问
题
05
(5)在对称轴上找一点P,使得|PA-PC|最大,求点P的坐标;
问
题
06
(6)在直线AC下方的抛物线上有一动点N,过点N的直线l//y轴,交线段AC于点M,求线段MN的最大值及此时点N的坐标.
问
题
07
(7)E是y轴上一动点,若BE=CE, 求点E的坐标.
问
题
08
(8)抛物线上有一动点P,过点P的作PM⊥x轴于M,交直线AC于点N,在线段PM、MN中,若其中一条线段是另一条线段的2倍,求点P的坐标.
问
题
09
(9)直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,求线段PH的最大值及此时点P的坐标.
问
题
10
(10)直线AC下方的抛物线上有一动点P,过点P作PH⊥AC于H,PG//y轴交AC于G,以GH、PH为邻边作矩形PEGH,求矩形PEGH
周长的最小值.
问
题
11
(11)在AC下方的抛物线上是否存在一点N,使得△CAN的面积最大?若存在,请求出△CAN的最大面积及点N的坐标.
问
题
12
(12)在AC下方的抛物线上是否存在一点N,使得四边形ABCN的面积最大?若存在,请求出四边形ABCN的最大面积
问
题
13
(13)在y轴上是否存在一点E,使得△ADE是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由;
问
题
14
(14)在y轴上是否存在一点F,使得△ADF是等腰三角形?若存在,求出点F的坐标;若不存在,请说明理由.
问
题
15
(15)抛物线上是否存在一点N(不与点C重合),使得 ?若存在,求出点N的坐标;若不存在,请说明理由;
问
题
16
(16)抛物线上是否存在一点H,使得 ?
若存在,求出点H的坐标;若不存在,请说明理由;
问
题
17
(17)抛物线上是否存在一点Q,使得 ?
若存在,求出点Q的坐标;若不存在,请说明理由;
问
题
18
(18)抛物线上是否存在一点E,使得BE平分△ABC的面积?若存在,求出点E的坐标;若不存在,请说明理由.
问
题
19
(19)抛物线上找一点P,作PM⊥x轴,交线段AC于点N,使AC平分△APM的面积.
问
题
20
(20)抛物线上找一点P,作PM⊥x轴,交线段AC于点H,使AC分△APM的面积为2:1两部分.
问
题
21
(21)在对称轴上有一点M,在抛物线上有一点N,若以A、B、M、N为顶点的四边形是平行四边形,求M、N的坐标;
问
题
22
(22)作垂直于x的直线x=-1, 交直线AC于点M,交抛物线于点N,以A、M、N、E为顶点作平行四边形,求第四个顶点E的坐标;
问
题
23
(23)点E是抛物线上一动点,点F在抛物线的对称轴上,若以C、D、E、F为顶点的四边形是菱形,求点E的坐标.
问
题
24
(24)在抛物线上能不能找到一点P,使得∠POC=∠PCO 若能,求出点P的坐标;若不能,请说明理由.
问
题
25
(25)在线段AC上是否存在点M,使得△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由;
问
题
26
(26)P是抛物线上一个动点,作PH⊥x轴于H,是否存在一点P,使得△PAH与△BOC相似 若存在,求出点P的坐标,说明理由.
问
题
27
(27)将△BOC绕平面内一点顺时针旋转90°,得到△B'O'P', 若△B'O'P'恰好有两个点同时落在抛物线上,求点O'的横坐标.
问
题
28
(28)将AD所在直线绕点A逆时针旋转45°,所得直线与抛物线交于点M,求点M的坐标.
问
题
29
(29)过点B的直线交直线AC于点M, 当直线AC与BM的夹角等于∠ACB的2倍时,直接写出点M的坐标.
问
题
30
(30)y轴上是否存在一点N, 使得∠BCO+∠BNO=∠BAC 若存在,直接写出点N的坐标.
演示完毕 感谢聆听
THANKS
同课章节目录
